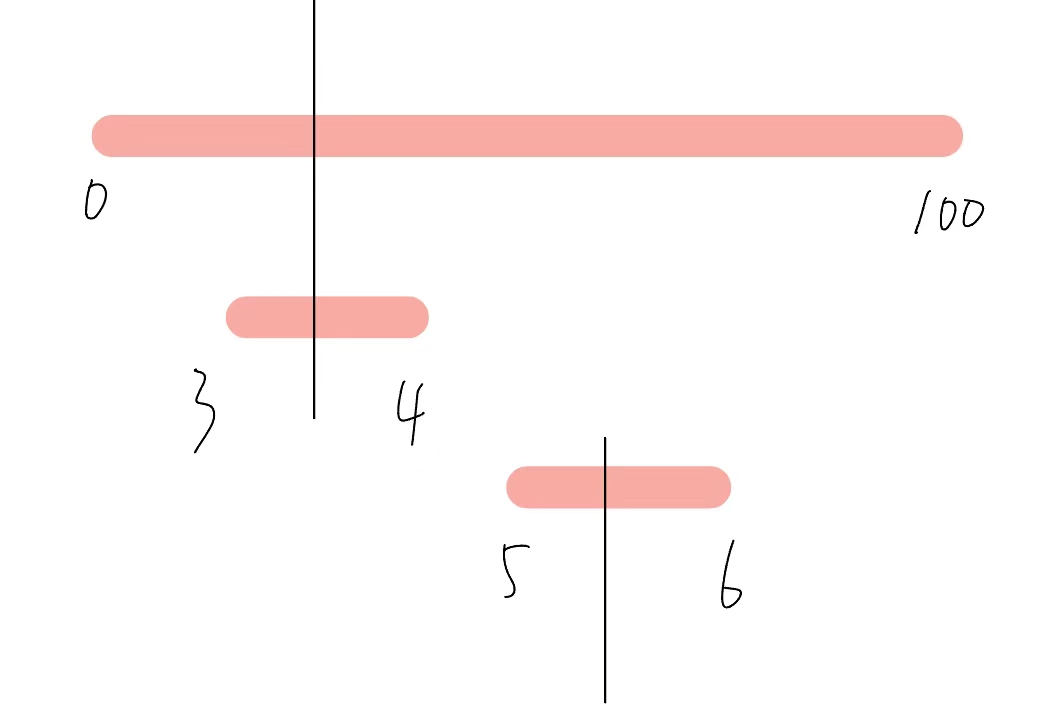LeetCode-JAVA

发表于 更新于 分类于

按照《Leetcode101-A Leetcode Gringding Guide》顺序记录。除此之外，开始正视代码书写规范。

ACM模式练习

1
2
3
next()、nextInt()、nextLine()都是Scanner内置的方法，他们的区别主要在于对于对空格的处理方式不同，以及返回值不同。
nextLine()方法，空格不作为两个字符串的间隔，而是看作字符串的一部分。
next()和nextInt()方法遇到空格时会停止读取，nextInt()的返回值为int类型，next()、nextLine()的返回值均为String类型。

1.A+B I

单纯简单计算两个数的和，但是有n组数据

输入包括两个正整数a,b(1 <= a, b <= 1000),输入数据包括多组。

1
2
3
4
5
6
7
8
9
10
11
import java.util.Scanner;
public class Main{ //注意这里没有()，没有String[] args
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        while(in.hasNext()){
            int a = in.nextInt();
            int b = in.nextInt();
            System.out.println(a + b);  // System.out.println(in.nextInt() + in.nextInt()); //或者可以把三行代码改成这个
        }
    }
}

2.A+B II

需要先声明要输入多少组数字之和

输入第一行包括一个数据组数t(1 <= t <= 100)
接下来每行包括两个正整数a,b(1 <= a, b <= 1000)

1
2
3
4
5
6
7
8
9
10
11
12
import java.util.Scanner;
public class Main{
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        int a = in.nextInt();
        while(a-- != 0){
            int b = in.nextInt();
            int c = in.nextInt();
            System.out.println(b + c);
        }      
    }
}

3.A+B III

和第一题不一样的是碰到0 0 则结束

输入包括两个正整数a,b(1 <= a, b <= 10^9),输入数据有多组, 如果输入为0 0则结束输入

1
2
3
4
5
6
7
8
9
10
11
12
import java.util.Scanner;
public class Main{
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        while(in.hasNext()){
            int a = in.nextInt();
            int b = in.nextInt();
            if (a == 0 && b == 0) break;
            System.out.println(a + b);
        }
    }
}

4.计算一系列数的和 I

先输入需要计算多少个数，然后求和，遇到第一个数为0则结束

输入数据包括多组。
每组数据一行,每行的第一个整数为整数的个数n(1 <= n <= 100), n为0的时候结束输入。
接下来n个正整数,即需要求和的每个正整数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import java.util.Scanner;
public class Main{
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        while(in.hasNext()) {
            int count = in.nextInt();
            if (count == 0) break;
            int sum = 0;
            while(count-- != 0){
                sum += in.nextInt();
            }
            System.out.println(sum);
        }
    }
}

5.计算一系列数的和 II

和第四题的区别是先声明需要输入多少组,而第四题是用0来结束的

输入的第一行包括一个正整数t(1 <= t <= 100), 表示数据组数。
接下来t行, 每行一组数据。
每行的第一个整数为整数的个数n(1 <= n <= 100)。
接下来n个正整数, 即需要求和的每个正整数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import java.util.Scanner;
public class Main{
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        int group = in.nextInt(); //这个是输入需要计算多少组
        while(group-- != 0) {
            int count = in.nextInt(); //每组多少个数字需要计算
            int sum = 0;
            while(count-- != 0){
                sum += in.nextInt();
            }
            System.out.println(sum);
        }
    }
}

6.计算一系列数的和 III

和4，5的区别是这个没有限制，只需要提供每组多少个数，也就是每行表示一组数据

输入数据有多组, 每行表示一组输入数据。
每行的第一个整数为整数的个数n(1 <= n <= 100)。
接下来n个正整数, 即需要求和的每个正整数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import java.util.Scanner;
public class Main{
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        while(in.hasNext()){
            int count = in.nextInt();
            int sum = 0;
            while(count-- != 0){
                sum += in.nextInt(); 
            }
            System.out.println(sum);
        }
    }
}

7.计算一系列数的和 IV

这个题和上面的区别是 没有指定每组数字有多少个

输入数据有多组, 每行表示一组输入数据。
每行不定有n个整数，空格隔开。(1 <= n <= 100)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import java.util.Scanner;
import java.util.Arrays;
public class Main{
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while(in.hasNextLine()){//注意这个Next是大写的
            String[] str = in.nextLine().split(" ");//在每个空格字符处进行分解
            //System.out.println(Arrays.toString(str));如果输入1 2 3，可以看到是处理成[1,2,3]
            int sum = 0;
            for(int i = 0; i < str.length; i++){
                sum += Integer.parseInt(str[i]);
            }
            System.out.println(sum);
        }
    }
}

8.字符串排序 I

只排序一组数据，先输入这组需要排序多少个字符

输入有两行，第一行n
第二行是n个字符串，字符串之间用空格隔开

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import java.util.Scanner;
import java.util.Arrays;
public class Main{
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        int count = in.nextInt();
        String[] str = new String[count];
        for(int i = 0; i < count; i++){
            str[i] = in.next();
        }
        Arrays.sort(str);//调库侠
        for(int i = 0; i < count; i++){
            System.out.print(str[i] + " ");//注意输出格式
        }
    }
}

9.字符串排序 II

和上一题的区别是不需要输入一组需要排序多少个字符 但是需要排序n组，也就是一次性输入一组的数据

多个测试用例，每个测试用例一行。
每行通过空格隔开，有n个字符，n＜100

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import java.util.Scanner;
import java.util.Arrays;
public class Main{
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        while(in.hasNextLine()){//注意这个Next是大写的
            String[] str = in.nextLine().split(" ");//注意这个next是小写的
            Arrays.sort(str);
            for(int i = 0; i < str.length; i++){
                System.out.print(str[i] + " ");//注意输出格式
            }
            System.out.print('\n');//注意输出格式
        }
    }
}

10.字符串排序 III

这个和上一题的区别是输出格式是逗号隔开，上一题是空格，但是注意的是上一题最后一个字符后面是空格，这一题如果按照上一题的逻辑去做会输出一个逗号，而题目不希望出现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import java.util.Scanner;
import java.util.Arrays;
public class Main{
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        while(in.hasNextLine()){
            String[] str = in.nextLine().split(",");
            Arrays.sort(str);
            for(int i = 0; i < str.length - 1; i++){
                System.out.print(str[i] + ",");
            }
            System.out.println(str[str.length - 1]);//避免最后一个后面有个逗号，同时加一个回车
        }
    }
}

11.A+B IV

和第一题的区别是数据范围不一样

1
2
3
4
5
6
7
8
9
10
11
import java.util.Scanner;
public class Main{ //注意这里没有()，没有String[] args
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        while(in.hasNext()){
            long a = in.nextLong();
            long b = in.nextLong();
            System.out.println(a + b);  // System.out.println(in.nextLong() + in.nextLong()); //或者可以把三行代码改成这个
        }
    }
}

360一道题 acm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/*
有一种特殊的DNA，仅仅由核酸A和T组成，长度为n，顺次连接

科学家有一种新的手段，可以改变这种DNA。每一次，科学家可以交换该DNA上两个核酸的位置，也可以将某个特定位置的核酸修改为另一种核酸。

现在有一个DNA，科学家希望将其改造成另一种DNA，希望你计算最少的操作次数。

ATTTAA
TTAATT
输出3

样例解释：
1.首先修改第一个位置的核酸（从A修改为T）
2.交换3和5位置的核酸
3.交换4和6位置的核酸
*/
import java.util.Scanner;
public class Main {
  public static void main(String args[]) {
    Scanner sc = new Scanner(System.in);
    String a,b;
    a = sc.nextLine();
    b = sc.nextLine();
    //return dna(a,b);
    System.out.println(dna(a,b));
  }
  public static int dna(String a, String b) {
    int c = 0;
    int d = 0;
    for (int i = 0; i < a.length(); i++) {
      if (a.charAt(i) == 'A' && b.charAt(i) != 'A') {
        c++;
      }
      if (a.charAt(i) == 'T' && b.charAt(i) != 'T') {
        d++;
      }
      
    }
    return Math.max(c,d);
  }
}

ACM 二叉树输入 前序遍历为例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
package hi;
import java.util.*;
public class tree {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        
        int n = sc.nextInt();
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = sc.nextInt();
        }
        
        TreeNode root = construct(arr);
        ArrayList<Integer> list = new ArrayList<>();
        preorder(root, list);
        System.out.print(list);
    }
    public static void preorder(TreeNode root, ArrayList<Integer> list) {//前序来举个例子
        if (root == null) {
            return;
        }
        list.add(root.val);
        preorder(root.left, list);
        preorder(root.right, list);
        
    }
    public static class TreeNode{
        int val;
        TreeNode left;
        TreeNode right;
        public TreeNode (int val){
            this.val = val;
        }
        public TreeNode (int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }
    public static TreeNode construct(final int[] arr) {
        List<TreeNode> treeNodeList = arr.length > 0 ? new ArrayList<>(arr.length) : null;
        TreeNode root = null;
        for (int i = 0; i < arr.length; i++) {
            TreeNode node = null;
            if (arr[i] != -1) {
                
                node = new TreeNode(arr[i]);
            }
            treeNodeList.add(node);
            if (i == 0) {
                root = node;
            }
            
        }
        
        for (int i = 0; i * 2 + 1 < arr.length; i++) {
            TreeNode node = treeNodeList.get(i);
            if (node != null) {
                node.left = treeNodeList.get(2 * i + 1);
                if (i * 2 + 2 < arr.length)//这个必须加上，不然越界了
                node.right = treeNodeList.get(2 * i + 2);
            }
        }
        return root;
    }

}

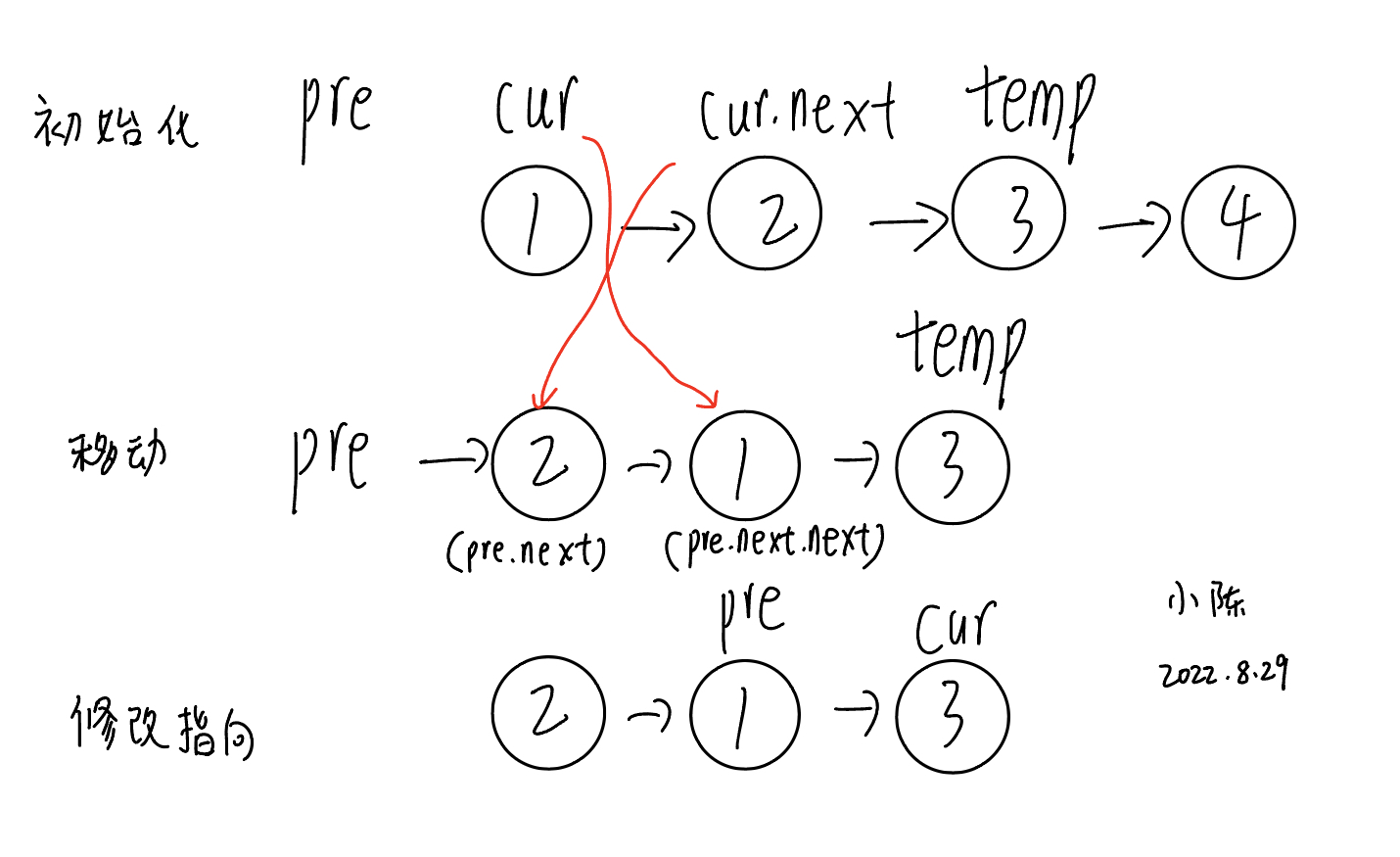
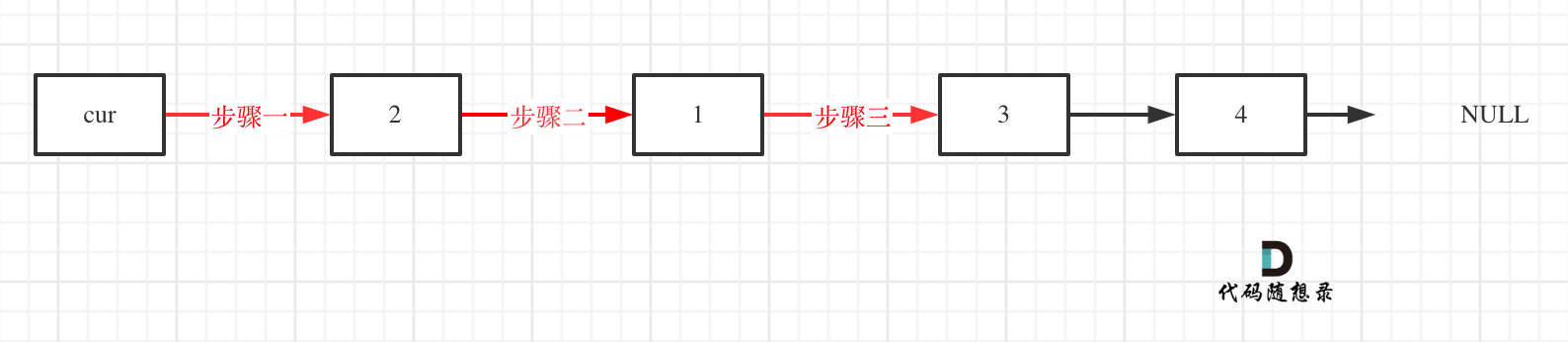
ACM 链表 反转链表为例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
package hi;
import java.util.Scanner;
public class listnode {
    static class ListNode{
        int val;
        ListNode next;
        ListNode(int val) {
            this.val = val;
        }
        ListNode(int val, ListNode next) {
            this.val = val;
            this.next = next;
        }
    }
    public static void main(String args[]) {
        Scanner sc = new Scanner(System.in);
        String[] param = sc.nextLine().split(" ");//输入的时候就是1 2 3 4 5
        ListNode dump = new ListNode(-1);
        ListNode cur = dump;
        for (String x : param) {
            cur.next = new ListNode(Integer.parseInt(x));
            cur = cur.next;
        }
        ListNode res = reverse(dump.next);
        while (res != null) {
            System.out.print(res.val);
            if (res.next != null) {
                System.out.print("->");
            }
            res = res.next;
        }
        
    }
    public static ListNode reverse(ListNode head) {
        ListNode pre = null;
        ListNode cur = head;
        while (cur != null) {
            ListNode temp = cur.next;
            cur.next = pre;
            pre = cur;
            cur = temp;
        }
        return pre;
    }

}

贪心算法

445 分发饼干 easy

依次满足胃口最小的孩子。可以想到先排序，然后再去分配。注意当满足了孩子后,cookie再加一，因为一个饼干只能用一次。

1
2
3
4
5
6
7
8
9
10
//知识点
/*
length()：String类的一个方法
字符串.length()
length() 方法用于返回字符串的长度。
长度等于字符串中 16 位 Unicode 代码单元的数量。

length：类的属性
数组.length
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int cookie = 0, child = 0;
        while(child < g.length && cookie < s.length){
            if(g[child] <= s[cookie]){
                child++;
            }
            cookie++;//饼干只能用一次，满足条件再加1。
        }
        return child;
    }
}

135 分发糖果 hard

首先建立一个数组，然后初始化为1，也就是每个人都先分到一颗糖。然后从左往右边遍历，如果右边的孩子得分高于左边，则右边的孩子糖果数=左边的孩子糖果数+1，注意这里不是直接加1.因为分数可能是依次增加，还要求分数高的糖果多。然后从右往左遍历，如果左边的孩子分数大于右边孩子分数并且左边孩子的糖果数不如右边孩子糖果数，则左边孩子糖果数=右边孩子糖果数+1，这种情况对应于左边分数大于右边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {//根据书上的思路写的，写法比较冗余。
    public int candy(int[] ratings) {
        int candys[] = new int[ratings.length];
        int count = 0; 
        for(int i = 0; i < ratings.length; i++){
            candys[i] = 1;
        }
        for(int i = 0; i < ratings.length-1; i++){
            if(ratings[i+1] > ratings[i]){
                candys[i+1] = candys[i] +1;
            }
        }
        for(int i = ratings.length-1; i > 0 ; i--){
            if(ratings[i-1] > ratings[i] && candys[i-1] <=  candys[i]){
                candys[i-1] = candys[i] +1 ;
            }
        }
        for(int i = 0; i < ratings.length; i++){
            count += candys[i]; 
        }
    return count;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {//这个有点不一样，分别创建两个数组，对应满足左右两个规则。然后分别取两个数组的最大值，为什么这样做可以？有个评论写得很清晰,如下。
/*
为什么取最大值是正确的思考：
很多人说这个问题显而易见，不值得讨论，但我相信还是有人像我一样不理解，在这里说一下我的想法
我疑惑的问题不是取最大值为啥是最优解，而是取最大值后为啥不影响某一规则的成立。
我们取序列中的任意两点，A B
如果 A > B ,则按照左规则处理后，B不会比A多；按照右规则处理后，A一定比B多，那么A一定会被更新（变大），但L、R规则仍然成立：B不会比A多，A一定比B多；
同理可讨论 A<B;
当 A == B，A、B的值无论如何更新，都不影响 L、R规则
综上，取最大值后不影响某一规则的成立。
*/

    public int candy(int[] ratings) {
        int[] left = new int[ratings.length];
        int[] right = new int[ratings.length];
        Arrays.fill(left, 1);
        Arrays.fill(right, 1);//把right数组全部填充为1，如果长度是长，则right=[1,1,1]
        for(int i = 1; i < ratings.length; i++)
            if(ratings[i] > ratings[i - 1]) left[i] = left[i - 1] + 1;
        int count = left[ratings.length - 1];
        for(int i = ratings.length - 2; i >= 0; i--) {
            if(ratings[i] > ratings[i + 1]) right[i] = right[i + 1] + 1;
            count += Math.max(left[i], right[i]);
        }
        return count;
    }
}

作者：jyd
链接：https://leetcode-cn.com/problems/candy/solution/candy-cong-zuo-zhi-you-cong-you-zhi-zuo-qu-zui-da-/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

435 无重叠区间 medium(可动态规划)

这里学到了Arrays.sort()新写法，开头一直纠结怎么把书上C++的排序用java表达(java用得少)。这里是要移除区间的最小个数，贪心的策略是：在选择要保留区间时，选择的区间结尾越小，余留给其他区间的空间就越大，就能保留更多的区间。首先对尾巴进行递增排序，也就是每个区间的第二个数字排序。然后对prve赋值为第一个区间的尾巴。开始进入for循环，如果第二个区间的头是小于prev，也就是在第一个的区间内，需要进行移除，如果大于了prev，则保留区间，然后prev赋值给第二个区间的尾巴，以此类推。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//首先是知识点笔记，部分来源于网络 Arrays.sort()
System.out.println(Arrays.deepToString(intervals));//这样可以输出二维数组的样子
System.out.println(Arrays.toString(intervals));//输出的貌似是地址，反正是这样的[[I@49993335, [I@20322d26, [I@192b07fd, [I@64bfbc86]
/*
方法一、使用Comparable接口：
让待排序对象所在的类实现Comparable接口，并重写Comparable接口中的compareTo() 。方法缺点是只能按照一种规则排序

方法二、使用Comparator接口 （推荐使用）
如果一个类要实现java.util.Comparator接口：它一定要实现
int compare(T o1, T o2) 函数，而另一个可以不实现（boolean equals(Object obj)） 。
使用编写排序方式类实现Comparator接口，并重写新Comparator接口中的compare()方法。优点：想用什么方式排就用什么方式排。

原理：观察Arrays.sort()源码如下：
public static <T> void sort(T[] a, Comparator<? super T> c) {
        if (c == null) {
            sort(a);
        } else {
            if (LegacyMergeSort.userRequested)
                legacyMergeSort(a, c);
            else
                TimSort.sort(a, 0, a.length, c, null, 0, 0);
        }
    }
所以，在传入要排序数组时，还可以传入一个Compartor接口（比较器），然后这个接口中要重写一个compare()方法，这个重写的compare()方法就是我们自己规定的比较规则。

实现Comparator接口，必须实现下面这个函数：
@Override
public int compare(CommentVo o1, CommentVo o2) {
           return o1.getTime().compareTo(o2.getTime());
}
这里o1表示位于前面的对象，o2表示后面的对象
返回-1（或负数），表示不需要交换01和02的位置，o1排在o2前面，asc
返回1（或正数），表示需要交换01和02的位置，o1排在o2后面，desc
*/
//所以本题的sort，比较尾巴就是interval1[1]，为了递增，左边尾巴减右边尾巴，负数就不需要交换，正数就交换。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {//这个是贪心策略写法
    public int eraseOverlapIntervals(int[][] intervals) {
        if(intervals.length == 0){
            return 0;
        }
        
        Arrays.sort(intervals,new Comparator<int []>(){
            public int compare(int[] interval1, int[] interval2){
                return interval1[1]-interval2[1];
            }
        });//学废了吗？
        int total = 0, prev = intervals[0][1];
        for(int i = 1; i < intervals.length; i++){
            if(intervals[i][0] < prev){
                total++;
            }
            else{
                prev = intervals[i][1];
            }
        }
       
    return total;
    }
}

605 种花问题 easy

虽说是easy题，但是发现自己想的bug很多，看到了一个很清晰的解题方法：跳格法。注意题目是不能打破原来的种植规则！。情况1：当index遇到1的时候，也就是至少隔一格才能种花，所以i要跳两格。情况2：当index遇到0时候，如果下一格为0，则可以种花（此时n-1），并且顺便跳两格，这里还有个情况就是如果已经是最后一格了，那就也能种花，一开始会想，万一最后一格的前面一格是1呢？注意这个情况不会发生，因为你是跳格法，你跳的index就代表是可能种花的，只需要考虑后面就行。如果下一个格子为1(比如0100)，则这格不能种花，则i要跳3格才可以种花。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {//这个写得比较清晰，但是冗余。
    public boolean canPlaceFlowers(int[] flowerbed, int n) {
         for(int i = 0; i < flowerbed.length && n >0;){
             if(flowerbed[i] == 1){
                 i += 2;
             }
             else if((flowerbed[i] ==0 && i == flowerbed.length-1) || (flowerbed[i] ==0 && flowerbed[i+1] == 0)){
                 n--;
                 i += 2;     
             }
             else if(flowerbed[i] ==0 && flowerbed[i+1] == 1){
                 i +=3;
             }
         }
        return n <= 0;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {//这个省略了点。
    public boolean canPlaceFlowers(int[] flowerbed, int n) {
         for(int i = 0; i < flowerbed.length && n >0;){
             if(flowerbed[i] == 1){
                 i += 2;
             }
             else if(i == flowerbed.length-1 ||  flowerbed[i+1] == 0){//因为你的flowerbed[i]不是1就是0，上一步已经判断好了是不是1，所以如果不是1的话自然跳到这里。
                 n--;
                 i += 2;     
             }
             else {
                 i += 3;
             }
         }
        return n <= 0;
    }
}

452 用最少数量的箭引爆气球 medium(和435相似)

这个题我的思路是，首先还是对尾巴进行升序排列，然后赋值prev给第一个数的尾巴，开始进行for循环比较第二个数，如果prev大于第二个数的头，也就是这个箭还是可以穿过去，不需要考虑尾巴，因为题目说了头一定比尾巴小。然后如果prev比头小，就说明穿不过去了，这时候就箭的数目加1.以此类推，这个注意count初始值为1，因为本身至少都需要一支箭，可以试试只有一个区间，在循环内counnt是不增加的。这里和435比较：435是不重叠区间，而这里刚好是重叠区间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {//看了一遍435后自己写的，注意这里的升序有点和435的不一样，因为会有一个用例存在溢出问题，如果按照435的写。[[-2147483646,-2147483645],[2147483646,2147483647]]，sort后是[[2147483646,2147483647],[-2147483646,-2147483645]]，因为他们相减后会溢出，所以用到小于来比较。
    public int findMinArrowShots(int[][] points) {
        if(points.length == 0){
            return 0;
        }
        Arrays.sort(points,new Comparator<int []>(){
            public int compare(int[] points1, int[] points2){
                if(points1[1] < points2[1]){
                    return -1;
                }
                else return 1;
            }
        });
       
        int count = 1,prev = points[0][1];
        for(int i = 1; i < points.length; i++){
           if(points[i][0] > prev){
                count++;
                prev = points[i][1];
            }           
        }
        return count;
    }
}

/*这个for循环就比较详细，但是没必要，增加运行的时间。
    for(int i = 1; i < points.length; i++){
            if(points[i][0] < prev){
                continue;
            }
            else if(points[i][0] > prev){
                count++;
                System.out.println(count);
                prev = points[i][1];
            }           
        }
*/

763 划分字母区间 medium

自己想的思路比较复杂，太冗余，而且可能考虑的东西不够全面。官方思路:首先用一个长度为26的数组a把每个字母的最后一个位置进行标记。设置start和end，开始循环字符串，访问每个字母，通过之前a来获取他的最后一个位置endc，令end=max（end，endc）。如果循环到i等于end，就说明之前的字母都包括在这个区间内，那就让长度写入partition，并令start=end+1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//知识点总结，
List<Integer> partition = new ArrayList<Integer>();
/*
List是一个接口
<>表示了List里面放的对象是什么类型的，上面List里面放的必须是Integer类型的

ArrayList类是一个特殊的数组–动态数组。通过添加和删除元素，就可以动态改变数组的长度。
优点：
1、支持自动改变大小 2、可以灵活的插入元素 3、可以灵活的删除元素
局限：
比一般的数组的速度慢一些；
可以调用 List接口里面的内置函数,add,get等方法
*/
last[s.charAt(i) - 'a'] = i;
/*
String s = "www.runoob.com";
char result = s.charAt(6);
输出为n
所以本题这样的做法，可以把每个字母的最后一个位置记录下来
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public List<Integer> partitionLabels(String s) {
          int start = 0, end = 0;
          int[] last =new int[26];
          List<Integer> partition = new ArrayList<Integer>();
          for(int i = 0; i < s.length(); i++){
              last[s.charAt(i) - 'a'] = i;
          }
          for(int i = 0; i < s.length(); i++){
              end = Math.max(end, last[s.charAt(i) - 'a']);
              if(i == end){
                  partition.add(end - start + 1);
                  start = end + 1;
              }
          }
          return partition;
    }
}

122 买卖股票的最佳时机2 easy(可动态规划)

还是没有独立想出来，想得太复杂，一直纠结怎么用区间来解答。官方解答太多数学公式，总体来说就是只要选择贡献大于0的区间，然后一直累加利润，但是这个做法是不知道第几次买卖的，只能求利润，对于负数，则和0比较就行。秒呀！

1
2
3
4
5
6
7
8
9
class Solution {
    public int maxProfit(int[] prices) {
        int price = 0;
        for(int i = 1; i < prices.length; i++){
            price += Math.max(0, prices[i] - prices[i-1]);
        }
    return price;
    }
}

406 根据身高重建队列 medium

网友思路：首先遇到这种数对问题，先排序。根据第一个元素正向排序，根据第二个元素反向排序，或者根据第一个元素反向排序，根据第二个元素正向排序，往往能够简化解题过程。在本题目中，先对数对进行排序，按照数对的元素 1 降序排序，按照数对的元素 2 升序排序。原因是，按照元素 1 进行降序排序，对于每个元素，在其之前的元素的个数，就是大于等于他的元素的数量，而按照第二个元素正向排序，我们希望 k 大的尽量在后面，减少插入操作的次数。小陈补充：如果第一个位置降序，第二个位置也降序排，再按照这样写法去插入的话，有部分用例是不能通过的，比如a[[7,0],[6,1],[5,2]]下一个待插入的数是[5,0]，按照算法应该插入到第一个位置，变成a[[5,0],[7,0],[6,1],[5,2]]这时候我们就发现[5,2]已经错误了，因为前面有三个数大于或者等于了。也就是你插入后，你得保证后面没有等于你的数插入，所以，第二个位置的排序，要升序！！！保证同胞小弟位置(第二个位置)先安排好。我们可以这样缕清楚，a里面已经插入的数都是比后面待插入的数大或者相等，如果后面待插入的数第二个位置比a的长度小，那么就是说他来选位置插，反之，他就插到最后面。

1
2
3
4
5
6
7
8
9
10
11
//知识点
//这个题可以学到compare对两个位置进行排序的写法，具体看下面的答案这里不多说
 List<int[]> list = new LinkedList<>();
/*
这个的话是双向链表，比创建数组a更加方便，创建数组的话，当你的情况是a的长度大小大于people[i][1]时，你是要插入到a的people[i][1]的位置，这时候你需要进行移动a[people[i][1]]以及后面的每个数据1位，然后才能插进去，这样麻烦。
最后转成list.toArray(new int[list.size()][]);返回即可。

可以对比763的
List<Integer> partition = new ArrayList<Integer>();

*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int[][] reconstructQueue(int[][] people) {
        Arrays.sort(people, new Comparator<int []>(){
            public int compare(int[] people1, int[] people2){
                if(people1[0] != people2[0]){
                    return people2[0] - people1[0];
                }
                else{
                    return people1[1] - people2[1];
                }
            }
        });
        List<int[]> list = new LinkedList<>();
        for(int i = 0; i < people.length; i++){
            if(list.size() > people[i][1]){
                list.add(people[i][1],people[i]);
            }
            else{
                list.add(list.size(),people[i]);
            }
        }
        return list.toArray(new int[list.size()][]);
    }
}

665 非递减数列 easy

第一次看题看错了，看成只移动一个数。这个题是改变一个数！虽然是easy，但是并不一定easy。网友解答很清晰：本题是要维持一个非递减的数列，所以遇到递减的情况时（nums[i] > nums[i + 1]），要么将前面的元素缩小，要么将后面的元素放大。但是本题唯一的易错点就在这，如果将nums[i]缩小，可能会导致其无法融入前面已经遍历过的非递减子数列；如果将nums[i + 1]放大，可能会导致其后续的继续出现递减；所以要采取贪心的策略，在遍历时，每次需要看连续的三个元素，也就是瞻前顾后，遵循以下两个原则：需要尽可能不放大nums[i + 1]，这样会让后续非递减更困难；如果缩小nums[i]，但不破坏前面的子序列的非递减性；算法步骤:遍历数组，如果遇到递减：还能修改：修改方案1：将nums[i]缩小至nums[i + 1]；修改方案2：将nums[i + 1]放大至nums[i]；不能修改了：直接返回false；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {//只能修改一次，让数组递增。
    public boolean checkPossibility(int[] nums) {
      if(nums.length == 1){
          return true;
      }
      boolean flag = nums[0] <= nums[1] ? true : false;//一开始第一个数小于第二个数，则拥有一次修改的机会。
      for(int i = 1; i < nums.length-1 ; i++){
          if(nums[i] > nums[i+1]){//开始出现递减情况。i大于后面一个数了
              if(flag){//如果拥有修改机会
                  if(nums[i+1] >= nums[i-1]){//如果i的后面一个数比i的前面一个数大的话，就说明他们是递增，让i缩小的话，也没有破坏非递减性，并且不影响i+1后面的序列。
                      nums[i] = nums[i+1];//这时候就让i缩小
                  }
                  else{
                      nums[i+1] = nums[i];//这个情况就是i后面的一个数比i前面的一个数小，但是同时i后面的数还小于i，所以只能让i后面的数扩大为i。
                  }
                  flag = false;//用掉了唯一的一次修改机会了
               }
               else {
                 return false;//再出现递减情况，但是已经没有修改机会了，直接返回false。
               }
           }
       }
        return true;//若nums(0) > nums(1)的话，flag是false，且后面没有出现递减，所以已经是可以用修改一次来递增，也就是把第一个数变成第二个数就满足，所以直接返回true。
    }
}

双指针

167 两数之和2 easy

注意题目给的数组是非递减顺序排列（也就是总体递增，然后可能有两个相邻的数是相等），所以思路上很简单，两个变量去追踪这个数组，一头一尾巴，如果两数之和小于target，左边就需要移动一位，反之则右边需要移动一位。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {//一开始根据书上思路写的，超时了~~~可能是暴力解法的原因，而且这个代码尚未验证是否正确。
    public int[] twoSum(int[] numbers, int target) {
        int j = numbers.length-1;
        int[] ans = new int[2];
        for(int i = 0; i < numbers.length-1 && i < j;){
           if(numbers[i] + numbers[j] == target)
           {
               ans[0] = i+1;
               ans[1] = j+1;
              
           }
           else if(numbers[i] + numbers[j] < target){
               i++;
           }
           else if(numbers[i] + numbers[j] > target){
               j--;
           }
        }
        return ans;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int i = 0;
        int j = numbers.length-1;
        //int[] ans = new int[2];
        while(i < j){
            int  sum = numbers[i] + numbers[j];
            if(sum == target){
                break;
            }
            else if(sum < target){
                i++;
            }
            else if(sum > target){
                j--;
            }
        }
        return new int[]{i + 1, j + 1};//这样就不用先去定义一个数组了。
    }
}

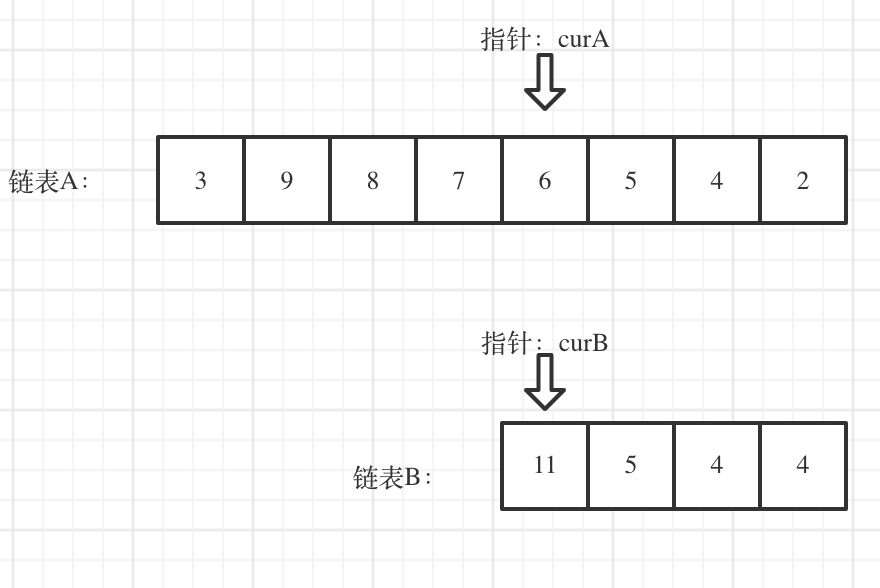
88 合并两个有序数组 easy

题目给的是两个非递减数组，思路是用m,n来指向两个数组的尾巴，还有pos来定位。首先要注意是在数组1的基础上去排，不需要额外开辟一个数组。pos定位在数组1的尾巴，开始对比两个数组的尾巴，哪个大就先复制过去。这里最后要注意，如果数组1复制完了，但是数组2还有，务必要记得继续复制。反之如果数组2复制完了，则不需要操作，因为数组1本身就是非递减，而且返回的数组就是他自己。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
         int pos = m-- + n-- -1;//这样写的话就少了一步，别忘了数组大小和数组位置是相差1.
         while(m >= 0 && n >= 0){
             nums1[pos--] = nums1[m] > nums2[n] ? nums1[m--] :nums2[n--];//注意是哪个大才会自减减哦。不是每次都自减减。
         }
         while(n >= 0){
             nums1[pos--] = nums2[n--];//务必不要忘记如果数组2还没复制完这个事！！！！！此时的数组1已经复制完啦！！！
         }
    }
}

142 环形链表2 medium

这个题涉及了一些数学计算，感谢网友讲解，这里复述一下：设置两个指针，一个为fast，一个为slow，fast每次走2步，slow每次走1步，设链表为a+b个节点，a为抵达环状的步数，b为环状的节点数。没有环状的链表很容易考虑，这里直接讲有环状的情况，也就是fast和slow会相遇：首先可以得到第一个关系式f=2s，这个是slow和fast的步数关系。第二个关系式是f=s+nb，因为fast比slow快，所以最终一定能追上，这时候呢，其实fast比slow多走了n个环。根据这两个关系，可以得到f=2nb,s=nb。接下来我们考虑，一个指针从头走到环状开头走过的步数k=a+nb，当n为0，也就是你走了a步到了环状的门口，然后n=1的话，你相当于绕了一圈环，然后又到了门口。现在有了三个表达式，从head结点走到入环点需要走:a + nb， 而slow已经走了nb（之前推了相遇的时候他们两个的关系），那么slow再走a步就是入环点了,如何知道slow刚好走了a步？fast从新从head开始和slow指针一起走，再相遇时刚好就是a步。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fast = head, slow = head;
        while(true){
            if(fast == null || fast.next == null){//注意别忘了是两个条件
                return null;
            }
            fast = fast.next.next;
            slow = slow.next;
            if(fast == slow){
                break;
            }
        }
        fast = head;
        while(slow != fast){
            fast = fast.next;
            slow = slow.next;
        }
        return fast;
        
    }
}

76 最小覆盖子串 hard

依旧是网友的思路，这个题在于需要考虑不少东西，这里简单描述一下：首先是建立一个128的ASCII列表，第一步先记录t中每个字符的数量。定义好l和r初始位置，还有用count去记录还需要的字符数量，这样就不用每次去查看need中哪个字符还大于0。开始while循环，用r去遍历整个S串，经过每个r的位置去提取字符c，首先判断c在need中的情况，如果是大于0，说明这个字符是符合t串的。然后减去一个count，代表已经找到了一个符合的字符，接下来是need中减去字符c的数量，注意，这里也包括不在t中的字符，不在t的中字符减去自然是为负数，代表这个字符是多余的。然后判断count为0的情况，count为0，代表已经找到符合的子串了，但是题目要求的size是最小的，所以可以缩减范围，当l小于r，并且里面有多余的字符，我们首先在need中加回去，然后移动l，然后开始重置size的大小，注意这时候的start变成新的l。接来下是移动l，看看还有没有更小的窗口，注意这里用start去保存这个开始的位置，而不是直接用l，这是有含义的，因为你的r是要遍历整个S串，这样你才知道哪个窗口是最小的，所以只有当size更小时候，我们才去更新更新start值，再加上size大小，就可以找到最小的串位置。这时候你无需当心l和r移动的位置了。务必务必注意，移动l的时候，请记得更新need和count以及l！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public String minWindow(String s, String t) {
    int[] need = new int[128];
    for (int i = 0 ; i < t.length() ; i++){
        need[t.charAt(i)]++;
    }
    int l = 0, r = 0, start = 0, size = Integer.MAX_VALUE, count = t.length();
    while (r < s.length()){
        char c = s.charAt(r);
        if (need[c] > 0){
            count--;
        }
        need[c]--;
        if(count == 0){
           while(l < r && need[s.charAt(l)] < 0){
               need[s.charAt(l)]++;
               l++;
           }
           if (r -l + 1 < size){
               size = r - l + 1;
               start = l;
           } 
           need[s.charAt(l)]++;
           count++;
           l++;
       }
       r++;
       
    }
    return size == Integer.MAX_VALUE ? "" : s.substring(start, start + size);
}}

633 平方数之和 medium

和167的很像，这里网友非常详细说明为什么i++和j–不会错过答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public boolean judgeSquareSum(int c) {
    long i = 0,j =(long) Math.sqrt(c);//如果直接写成c，会超时。理论上也是应该对的。
    while(i <= j){
       long sum = i*i + j*j;
       if( sum == c ){
           return true;
       }
       else if( sum < c ){
           i++;
       }
       else {
           j--;
       }
    }
    return false;
    }
}

680 验证回文字符串2 easy

这个题虽然是简单题，但是还是看了网友思路：用双指针去对比，一个在头l，一个在尾巴r，当遇到不相等的情况，我们可以让l加1个位置，或者让r减去一个位置，因为题目说了可以最多删除一个字符，然后再用一个函数去对比子字符串。这里我一开始想到的是用一个计数器去判断删除的次数，后来发现其实不需要，比如abxbgga，要删除两次才行，你只要仔细看代码，发现只要一次之后不行就直接false了，所以不用考虑加一个计数器的问题，那么删除一个字符是体现在r-1或者l+1上

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public boolean validPalindrome(String s) {
    int l = 0, r = s.length()-1;
    while(l < r){
        if(s.charAt(l) != s.charAt(r)){
            return judegesub(s, l+1, r) || judegesub(s, l, r-1);
        }
        l++;
        r--;
    }
    return true;
    }
    public boolean judegesub(String s, int l, int r){
        while(l < r){
            if(s.charAt(l) != s.charAt(r)){
                return false;
            }
        l++;
        r--;
        }
        return true;
    }
}

524 通过删除字母匹配到字典里最长单词 medium

这个题我一开始考虑的是，首先跟上一个题的区别是，这个题的意思是可以删除好几个元素，然后第二个不同的是，这个题有多个词，是不是要用暴力算法一个个去看？看了官方解答后，发现被上一题绕进去了。大概重复下解法：用双指针思路，i和j分别指向t(字典中的词)和s的第一个字母，注意这里是每个字典的词都会遍历，然后如果匹配，则i和j同时移动一位，如果不匹配，i不动，j+1。直到最后i要是等于这个词的长度的话，就代表全部匹配到。注意这里是长度，长度和单词最后一个字符位置是相差1的。题目中说要长度最长和序号最低的。所以自然有一个长度对比以及序号对比，序号对比是用compareTo函数，这个是对比ASCII对比，也就是序号在前的话是小于0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//知识点
class Solution {
    public String findLongestWord(String s, List<String> dictionary) {
        for (String t : dictionary) {
          System.out.print(t);
          System.out.print(" ");
        }  
    }
}
//输入是["ale","apple","monkey","plea"]这里会依次输出ale apple monkey plea 

关于compareTo:
返回值是整型，它是先比较对应字符的大小(ASCII码顺序)如果第一个字符和参数的第一个字符不等，结束比较，返回他们之间的长度差值，如果第一个字符和参数的第一个字符相等，则以第二个字符和参数的第二个字符做比较，以此类推,直至比较的字符或被比较的字符有一方结束。

如果参数字符串等于此字符串，则返回值 0；
如果此字符串小于字符串参数，则返回一个小于 0 的值；
如果此字符串大于字符串参数，则返回一个大于 0 的值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public String findLongestWord(String s, List<String> dictionary) {
        String res = "";
        for (String t : dictionary) {
            int i = 0, j = 0;
            while (i < t.length() && j < s.length()) {
                if (t.charAt(i) == s.charAt(j)) {
                    ++i;
                }
                ++j;//注意这里，如果匹配的话，j是在这里++，而不是在上面的if语句，因为这里还有一个就是如果不匹配的话，j也要++，而这时候i不变，所以这个写法可以同时满足两个条件
            }
            if (i == t.length()) {
                if (t.length() > res.length() || (t.length() == res.length() && t.compareTo(res) < 0)) {
                    res = t;
                }
            }
        }
        return res;
    }
}

二分查找

69 Sqrt(x) easy

这个题是看了官方解法，其实思路就是二分法，每次寻找中间值，如果中间值的平方小于输入值，则把左边的边界设置为mid+1，反之如果大于输入值，则把右边界设置为mid-1，这里注意一个问题就是mid * mid前面要加long，不然超过范围。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid <= x){
                ans = mid;
                l = mid + 1;
            }else {
                r = mid - 1;
            }
        }
    return ans;
    }
}

34 在排序数组中查找元素的第一个和最后一个位置 medium

这里有一个网友的二分法模板，关于这个题，分了两步，首先是寻找第一个target，循环内部条件是num[mid]大于等于target，然后用模板1，寻找最后出现的target，用模板2。至于为什么分开模板1和2，有个网友解释很清楚：因为取左边第一个target时，当nums[mid]==target时，中间位置的右边元素一定不是target出现的第一个位置，所以下次搜索区间是[left,mid],right=mid;取最后一个target时，当nums[mid]==target时，中间位置的左边元素一定不是target出现的最后一个位置，所以下次搜索区间是[mid，right],left=mid。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//模板1
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = (l + r)/2;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

//模板2
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = ( l + r + 1 ) /2;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

/*
总结归纳：当l=mid时，mid=(l+r+1)/2，当l=mid+1，mid=(l+r)/2，至于为什么请看网友解释，这个题要多次理解。
这里复制了网友的解释：什么时候用模板1，什么时候用模板2？
假设初始时我们的二分区间为[l,r]，每次二分缩小区间时，如果左边界l要更新为 l = mid，此时我们就要使用模板2，让 mid = (l + r + 1)/ 2，否则while会陷入死循环。如果左边界l更新为l = mid + 1,此时我们就使用模板1，让mid = (l + r)/2。因此，模板1和模板2本质上是根据代码来区分的，而不是应用场景。如果写完之后发现是l = mid，那么在计算mid时需要加上1，否则如果写完之后发现是l = mid + 1，那么在计算mid时不能加1。

*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int[] searchRange(int[] nums, int target) {
        if (nums.length == 0) return new int[]{-1, -1};//上来就要记住这个。
        int l = 0, r = nums.length - 1;
        while (l < r){
            int mid = (l + r) / 2;
            if (nums[mid] >= target) r = mid ;//比目标值大，则寻找左区间，右边变为mid，左边不动。
            else l = mid + 1;//比目标值小，寻找右区间，左边变成mid+1，右边不动。
        }
        if (nums[r] != target) return new int[]{-1,-1};//这个特别容易忘记的。
        int L = r;
        l = 0; r = nums.length - 1;
        while (l < r){
            int mid = (l + r + 1) / 2;
            if (nums[mid] <= target) l = mid ;//比目标值小，寻找右区间，左边变成mid，右边不变。
            else r = mid - 1;//比目标值大，寻找左区间，右边变成mid-1，左边不变。
        }
        return new int[]{L,r};

    }
}

81 搜索旋转排序数组 II medium

找数组的目标数，这个题就是说本来的数组是增序的，但是现在相当于在中间断开，然后再连起来，就变成一个旋转数组。所以，旋转数组的特性的有一部分是增序的。先依旧找到中点位置，后面解释看代码。这个coder把一些情况得很清楚。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/*
解题思路：
本题是需要使用二分查找，怎么分是关键，举个例子：

第一类
1011110111 和 1110111101 这种。此种情况下 nums[start] == nums[mid]，分不清到底是前面有序还是后面有序，此时 start++ 即可。相当于去掉一个重复的干扰项。
第二类
22 33 44 55 66 77 11 这种，也就是 nums[start] < nums[mid]。此例子中就是 2 < 5；
这种情况下，前半部分有序。因此如果 nums[start] <=target<nums[mid]，则在前半部分找，否则去后半部分找。
第三类
66 77 11 22 33 44 55 这种，也就是 nums[start] > nums[mid]。此例子中就是 6 > 2；
这种情况下，后半部分有序。因此如果 nums[mid] <target<=nums[end]。则在后半部分找，否则去前半部分找

*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public boolean search(int[] nums, int target) {
        int start = 0, end = nums.length - 1;
        while (start <= end) {
            int mid = (start + end) / 2;
            if (nums[mid] == target){
                return true;
            }
            if (nums[start] == nums[mid]){//因为数组会存在重复数字，如果中点和左端相等，我们不能确定在左区间全部相等，还是右边区间全部相等，这种情况，可以把start右移动一个，当然这种操作我们不能说是完全的二分法，这个题只是部分地方用到二分法。
                start++;//无法判断哪个区间是增序的
            } else if (nums[mid] <= nums[end]) {//右区间是增序的
                if (target > nums[mid] && target <= nums[end]) {//然后在右区间内判断target，用二分法。target在mid和end中间，这里需要注意，target是要小于等于end。我觉得要这么去想，你想如果都等于mid，那肯定是直接返回true，所以有mid比较这边是开区间
                    start = mid + 1;//就让start移动到mid右边
                }else {
                    end = mid -1;//反之，让end移动到mid左边
                }
            } else {//这个情况则是左区间增序
                if (target < nums[mid] && target >= nums[start]) {//这里需要注意，target是要大于等于start
                    end = mid - 1;
                } else {
                    start = mid + 1;
                }
            }
        }
    return false;
    }
}

154 寻找旋转排序数组中的最小值 II hard

这个题也是旋转数组，和上个题的区别是，1.上个题是找target，这个题是找最小值。2.这个题旋转多次。这个作者解释得不错，把作者思路拷贝到了下面了，注意一下这个题，旋转后每个数字的序号保持原来不变，也就是原来是0位置，旋转后序号还是0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/*
    -思路-
    旋转数组肯定将nums分为两个有序的数组，分为别nums1和nums2。并且假设nums1中的元素均大于等于nums2中的元素
    那么我们要求的元素就是nums2的首元素
    --步骤--
    如果nums[mid] > nums[right],说明此时的mid严格的在nums1当中。（这时候最小值在[mid,right]上？所以把区间缩到这来，我理解的），那么nums2的首元素设为i的话，就应当是：mid < i <= right。
    取left = mid + 1;附其他解释：当 nums[mid] > nums[right]时，mid一定在第 1 个排序数组中，i 一定满足 mid < i <= right，因此执行 left = mid + 1；


    如果nums[mid] < nums[right],说明此时的mid严格的在nums2当中。（这时候最小值在[left,mid]上？所以把区间缩到这来，我理解的）也就是：mid <= i < right
    取right = mid(注意这里没有mid-1)；附其他作者解释：当 nums[mid] < nums[right] 时，mid 一定在第 2 个排序数组中，i一定满足 left < i <= mid，因此执行 right = mid；

    如果nums[mid] == nums[right],细分为三种情况。
        情况一：[1,1,1,1,1,1,1,1]
        情况二：[4,5,6,7,1,1,1,1,1,1]
        情况二：[4,5,6,7,0,1,1,1,1,1]
    取right--便可，这个很关键！！！！

    另外一个作者解释了为什么这样：
    我们采用 right = right - 1 解决此问题，证明：
    此操作不会使数组越界：因为迭代条件保证了 right > left >= 0；
    此操作不会使最小值丢失：假设 nums[right]是最小值，有两种情况：
    若 nums[right]是唯一最小值：那就不可能满足判断条件 nums[mid] == nums[right]，因为 mid < right（left != right 且 mid = (left + right) // 2 向下取整）；
    若 nums[right]不是唯一最小值，由于 mid < right 而 nums[mid] == nums[right]，即还有最小值存在于 [left, right - 1][left,right−1] 区间，因此不会丢失最小值。

作者：jyd
链接：https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array-ii/solution/154-find-minimum-in-rotated-sorted-array-ii-by-jyd/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
*/
class Solution {
    public int findMin(int[] nums) {
        int left = 0, right = nums.length - 1;
        while (left < right) {
            int mid = (left + right) / 2;
            if (nums[mid] == nums[right]) {
                right--;
            } else if (nums[mid] < nums[right]) {
                right = mid;
            } else if (nums[mid] > nums[right]) {
                left = mid + 1;
            }
        }
    return nums[right]; //貌似nums[left]也是可以的。其实看了下，最后left=mid+1也就是等于right，所以这样也就是两种写法都是一样。
    }
}

540. 有序数组中的单一元素 meidum

这个题是找到唯一的单身狗，注意题目是升序的，不过貌似与升序没关系。这里先整理下官方的清晰解答：因为这个模块是讲二分法，所以不讲解暴力算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/*
首先要知道，这个数组一定是奇数个，因为只有一个单身狗！
用 halvesAreEven = (right - mid) % 2 == 0来判断哪一侧元素为奇数，因为单身狗肯定在这一侧。
情况1：mid 和 mid+1是同元素。然后mid元素把两侧都分为偶数个，当我们把mid+1拿掉后，右侧就变成奇数个了，也就是右侧肯定存在单身狗，设置left = mid + 2
情况2；mid 和 mid+1是同元素。然后mid元素把两侧都分为奇数个，当我们把mid+1拿掉后，右侧是偶数个，所以左侧存在单身狗，设置right = mid - 1 
情况3：mid 和 mid-1是同元素。然后mid元素把两侧都分为偶数个，当我们把mid-1拿掉后，左侧就是奇数个了，所以左侧存在单身狗，设置right = mid - 2
情况4：mid 和 mid-1是同元素。然后mid元素把两侧都分为奇数个，当我们把mid-1拿掉后，右侧就存在单身狗，所以left = mid + 1
首先判断mid和左边还是右边的元素相等，然后通过halvesAreEven判断左右两侧是奇还是偶。
这里只举例情况1和2，因为这是放在一起的。现在已经知道了mid和mid+1相等，然后再想，如果mid把两侧分为了偶数个(单纯讲个数，与数组位置无关)，也就是mid的位置是一个偶数(数组从0计算)，然后整个数组肯定是奇数个，也就是最后一个数的位置也是偶数，所以当halvesAreEven为true，就说明符合情况1，反之符合情况2。
注意写代码的时候别忘了mid就是单身狗的情况。

下面这个方法也是二分，但是仅对偶数索引进行二分搜索，比上面的方法简洁，而且不用单独考虑mid是单身狗的情况，因为else就是包含了mid是单身狗或者左侧存在单身狗。
然后就是简洁点，整理下上面的思路，我们确保mid是偶数的位置，如果是奇数就减去1，然后检查 mid 的元素是否与其后面的索引相同。如果相同，则我们知道 mid 不是单个元素。
且单个元素在 mid 之后。则我们将 left 设置为 mid + 2。
如果不是，则我们知道单个元素位于 mid，或者在 mid 之前。我们将 right 设置为 mid。
一旦 left == right，则当前搜索空间为 1 个元素，那么该元素为单个元素，我们将返回它。
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
/*
知识点：int mid = left + (right - left) / 2;
为什么前面还要加left?因为防止超出整型数据溢出。可以看看前面的题有没有这种情况！！
*/
    public int singleNonDuplicate(int[] nums) {
        int left = 0, right = nums.length - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (mid % 2 == 1 ) mid--;
            if (nums[mid] == nums[mid+1]) {
                left = mid + 2;
            } else {
                right = mid;
            }
        }
    return nums[right];//left也可以，第一次写的时候写成了mid，先不说结果对不对，这里语法就存在问题，因为mid在while里面，所以系统会检测不到mid，是一个局部变量。
    }
}

4 寻找两个正序数组的中位数 hard

这个题虽然看上去是可以合并起来去找，但是，由于有时间复杂度的要求，所以用二分法比较好，坦白说，确实hard。详细解释点击这里看解法三。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
//用的代码是官方的，但是上面说的解释更清楚。
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int length1 = nums1.length, length2 = nums2.length;
        int totallength = length1 + length2;
        if (totallength % 2 == 1){//两个数组长度和为奇数情况
           int midIndex = totallength / 2;//注意totallength是个数，而不是数组中的序号(从0开始)。
           double median = getKthElement(nums1, nums2, midIndex + 1);
           return median;
        } else {//两个数组长度合为偶数情况
            int midIndex1 = totallength / 2 -1, midIndex2 =totallength / 2;
            double median = (getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0;
            return median;
        }

    }
    public int getKthElement(int[] nums1, int[] nums2, int k) {
        //下面是官方写的
        /* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
         * 这里的 "/" 表示整除
         * nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
         * nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
         * 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
         * 这样 pivot 本身最大也只能是第 k-1 小的元素
         * 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组
         * 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组
         * 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数
         */

        int length1 = nums1.length, length2 = nums2.length;
        int index1 = 0, index2 = 0;
        int kthElement = 0;

        while (true) {//边界情况
            if (index1 == length1) {
                return nums2[index2 + k - 1];
            }
            if (index2 == length2) {
                return nums1[index1 + k - 1];
            }
            if (k == 1) {//当k剩下一个的时候，也就是比较剩下哪个数谁比较小。
                return Math.min(nums1[index1], nums2[index2]);
            }

            //正常情况 
            int half = k / 2;
            int newIndex1 = Math.min(index1 + half, length1) - 1;// k/2-1
            int newIndex2 = Math.min(index2 + half, length2) - 1;// k/2-1
            int pivot1 = nums1[newIndex1] ,pivot2 = nums2[newIndex2];
            if (pivot1 <= pivot2) {
                k = k -(newIndex1 - index1 + 1);
                index1 = newIndex1 + 1;
            } else {
                k = k -(newIndex2 - index2 + 1);//加1是因为要去掉pivot这个元素
                index2 = newIndex2 + 1;
            }
        }//这个是while语句的结束
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
//由于这个题实在是费脑，这里详细举例子，按照代码思路一步步来
nums1:1 3 4 9
nums2:1 2 3 4 5 6 7 8 9
开始计算： 
length1=4,length2=9
totallength=13
判断为奇数，midIndex=6 传入到子函数(nums1，nums2,6+1)//也就是第7个数是中位数

下面是子函数循环情况

下面说的 排 是指两个数组合并起来，从小到大排第几个的意思
length1=4,length2=9
正常情况
第一轮while
half=7/2=3
newIndex1=3-1=2,newIndex2=3-1=2//比较nums1[k/2-1],nums2[k/2-1]的元素，本题也就是nums1[2],nums2[2]

[pivot]元素
1 3 [4] 9
1 2 [3] 4 5 6 7 8 9    可以看出nums2[2]的更小，把nums2[2]及其前面元素全部去掉，然后更新index2和k

这里需要理解为什么更新k和index2，我们要找的数是排序第七个(不是从0计算)的数，然后分别比较两个数组的nums[k/2-1]
nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个，本题也就是2个
nums2 中小于等于 pivot2 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个，本题也就是2个
然后取两个数组中比较小的pivot，本题是num2[2],可以推导，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个，也就是全部元素合并后小于等于nums2[2]元素的不超过5个，如果按照等式左边是为4个，因为是整除，如果按照等式右边就直接是5个。
这样的话，即便取pivot本身最大也只能是第 k-1 小的元素，也就是6，但是按照上一行的分析，pivot元素是排第5或者第6，本题的话实际是排第5。
总之还不是第七个我们要找的元素。那么可以完全排除nums[2]和左边的元素，这时候就要更新k和index2
k更新：因为本身要找第7个元素，现在已经排除了3个元素了，所以k=7-3=4，也就是在剩下的数组中找排第四个的元素，具体写法是7-（2-0+1)=4
index2更新： index2=2+1=3，也就是从nums2[3]开始
index1依旧为0

第二轮while   
half=4/2=2
newIndex1=0+2-1=1,newIndex2=3+2-1=4
下面标记|，代表左边的元素也就消除。
1 [3] 4 9
1 2 3 | 4 [5] 6 7 8 9
经过比较后，nums1[1]及其左边消除
k更新：因为本身要找第4个元素，现在已经排除了2个元素了，所以k=4-2=2，也就是在剩下的数组中找排第二个的元素，具体写法是4-（1-0+1)=2
index1更新： index1=1+1=2，也就是从nums1[2]开始
index2依旧为3

第三轮while
half=2/2=1
newIndex1=2+1-1=2,newIndex2=3+1-1=3
1 3 | [4] 9
1 2 3 | [4] 5 6 7 8 9
这里pivot元素相等，我们就假设上面的4大于下面的4，由于两个数相等，所以我们无论去掉哪个数组中的都行，因为去掉 1 个总会保留 1 个的，所以没有影响。
经过比较后，nums2[3]及其左边消除。
k更新：因为本身要找第2个元素，现在已经排除了1个元素了，所以k=2-1=1，也就是在剩下的数组中找排第二个的元素，具体写法是2-（0-0+1)=1
index2更新： index2=3+1=4，也就是从nums2[4]开始
index1依旧为2

第四轮while
k已经等于1了，直接找剩下比较小的数就行。
1 3 | [4] 9
1 2 3 4 | [5] 6 7 8 9
答案就是4


当然还有注意边界的情况，本题没有涉及。
所谓边界的问题,也就是有可能其中一个数组过小，然后进行更新的时候会发现越界，这时候也就是这个小的数组数组全部已经小于第K个数据，然后我们之后关注大的数组找到k就行。

常用排序算法

排序算法

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//本代码是可执行代码，后面的排序算法可以直接用在本模板调用。
//快速排序就是每次把第一个数选为枢轴元素，然后左右扫描，右边扫描比它小的交换，左边扫描比它大的交换，最后放到正确的位置，最终左边的元素都比它小，右边的元素都比它大，然后左右递归。
import java.util.Arrays;
public class sort {
    public static void main(String[] args) {
        int arr[] = {6,7,8,1,2,3,9,10,0,4,6,8,7,99,77,44};//初始化数组时用new与不用new是没区别的
        int temp[] = new int[arr.length];
        int size = arr.length;
        quick_sort(arr, 0, size);//实现快速排序
        //insertion_sort(arr,size);//实现插入排序
        //merge_sort(arr, 0, size, temp);//实现归并排序
        //bubble_sort(arr, 0, size);//实现冒泡排序
        //select_sort(arr,size);实现选择排序
        System.out.println(Arrays.toString(arr));//输出结果
    }
    public static void quick_sort(int[] arr,int left, int right) {//左闭右闭区间，也就是right一开始输入的是size
        if (left + 1 >= right) {
            return;
        }
        int first = left, last = right - 1, key = arr[first];
        while (first <last) {
            while (first < last && arr[last] >= key) {//右边扫描
                --last;
            }
            arr[first] = arr[last];
            while (first < last && arr[first] <= key) {//左边扫描
                ++first;
            }
            arr[last] = arr[first];
        }
        arr[first] = key;//把枢轴元素放到正确的位置
        quick_sort(arr, left, first);//左边递归
        quick_sort(arr, first + 1, right);//右边递归
    }

插入排序

1
2
3
4
5
6
7
8
9
10
//从第二个数开始，只要比前面小就一直交换。这样每轮的前i个数都是从小到大排好序，就好像插队一样，一直插。
public static void insertion_sort(int[] arr, int size){
    for (int i = 0; i < size; i++) {
        for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--) {//别忘了防止越界的问题，j>0。
            int temp = arr[j-1];
            arr[j-1] = arr[j];
            arr[j] = temp;
        }
    }
}

选择排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//每次把未排序中最小的数选出来，然后和前面未排序第一个数交换。
public static void select_sort(int[] arr,int right) {
    int small;
    for (int i = 0; i < right - 1; i++) {//这里写成right也是没有问题的，但是right的话理论上来说多做了一步无用功
        small = i;
        for (int j = i + 1; j < right; j++) {
            if (arr[j] < arr[small]) {
                int temp = arr[j];
                arr[j] = arr[small];
                arr[small] = temp;
            }
        }
    }
}

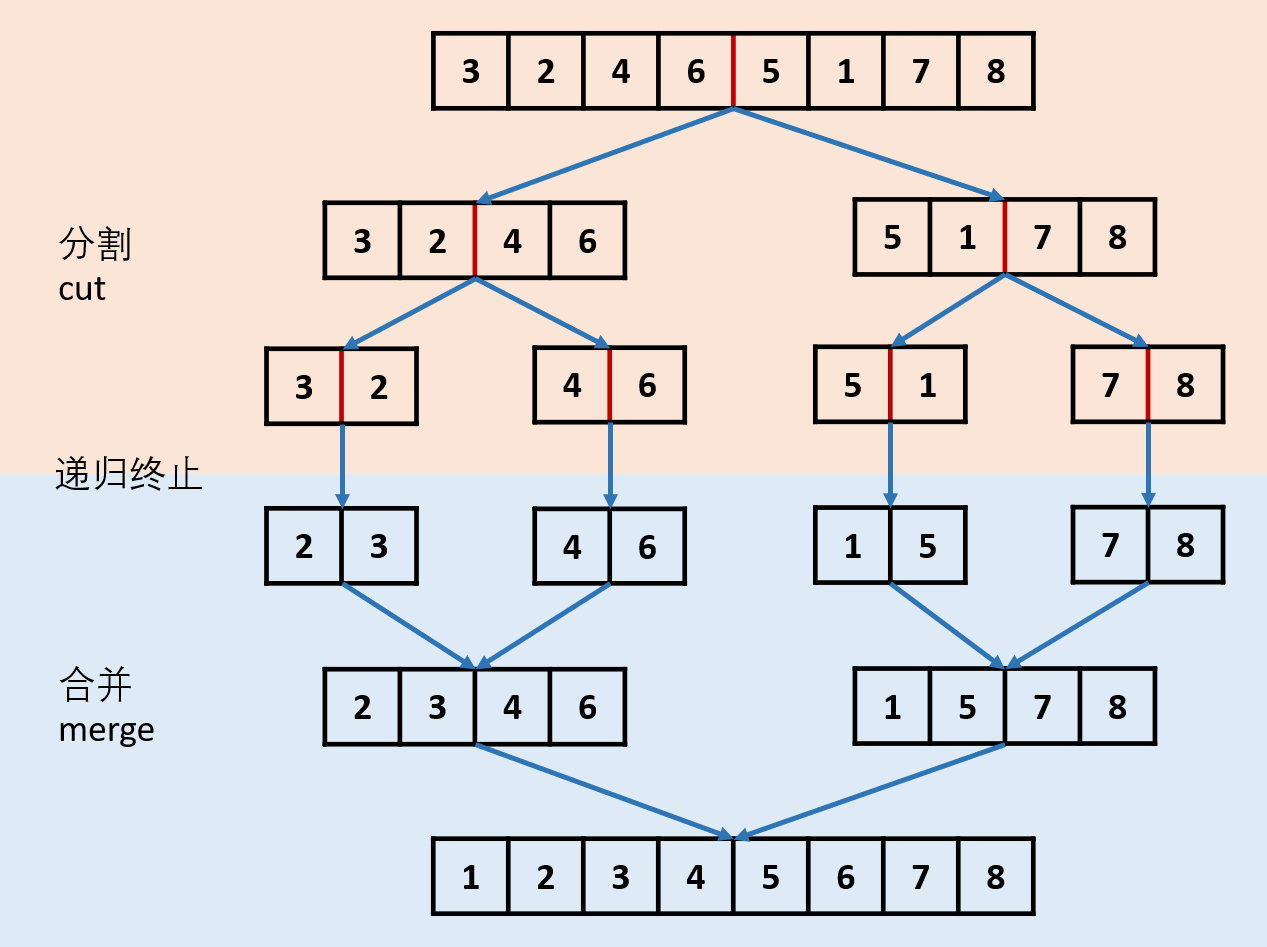
归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/*
归并排序采用了分治的思想。将数字分成许多小块，每块排序，然后再把块逐步合并起来。
重点：最终合并的时候需要一个临时数组来存储合并数据。合并的时候左右两边是两个排好序的数组，现在要把它们组合起来。关键点就在于判断每一次放入临时数组的是左侧还是右侧的数据。
first和second代表左右侧
如果左侧比右侧小，而且此时两个数组都没越界，左侧的数输入到temp。
如果左侧越界，那么右侧读入。
如果右侧越界，那么左侧读入。
综合起来，读入左侧数据的条件即为右侧越界或者左侧没越界且左侧比右侧小。
最后再改变nums
*/
void merge_sort(vector<int> &nums, int left, int right, vector<int> &temp)
{//C++版本
    if (left + 1 >= right) {
       return;
    }
    int mid = left + (right - left) / 2;//寻找中间数的位置

    merge_sort(nums, left, mid, temp);//左侧递归
    merge_sort(nums, mid, right, temp);//右侧递归

   int first = left, second = mid, i = left;
   while (first < mid || second < right) {   //first是左侧边界开始，second是右侧边界开始
    if (second >= r || (nums[first] <= nums[second] && first < mid)) {//右侧越界或者是 左侧没有越界，并且左侧的first位置比右侧的second位置小
        temp[i++] = nums[first++];//那就左侧写入temp
    } else {
        temp[i++] = nums[second++];
    }
   }
   for (i = l; i < r; ++i) {
        nums[i] = temp[i];
   }
}
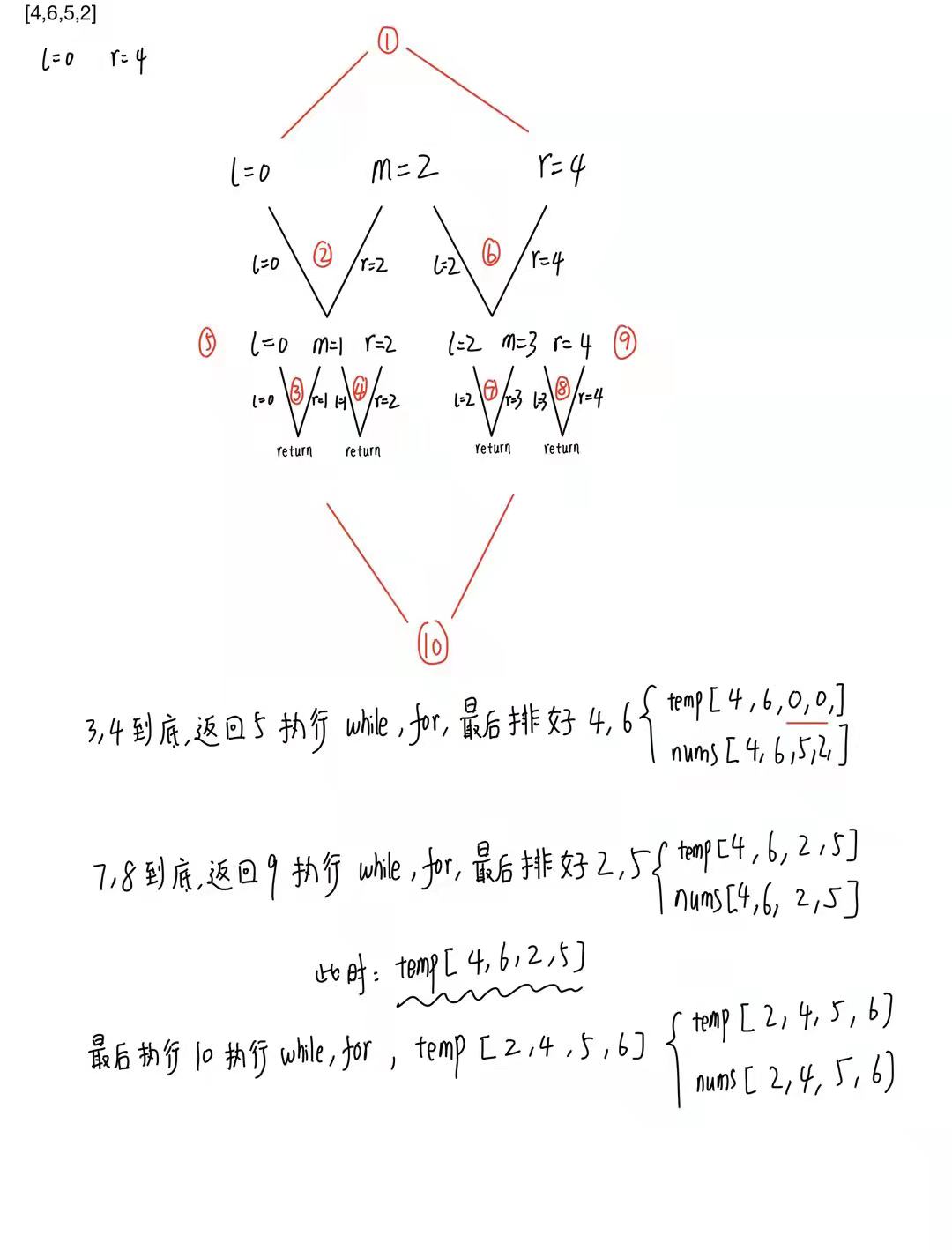
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//java
public static void merge_sort(int[] arr,int left, int right, int[] temp) {//左闭右开区间哦，所以right进来是size
    if (left + 1 >= right) {
        return;
    }
    int mid = left + (right - left) / 2;
    merge_sort(arr, left, mid, temp);//别忘了左闭右开区间
    merge_sort(arr, mid, right, temp);
    int first = left, second = mid, i = left;
    while (first < mid || second < right) {
        if (second >= right || (arr[first] <= arr[second] && first < mid)) {
            temp[i++] = arr[first++];
        } else {
            temp[i++] = arr[second++];
        }
    }
    for (i = left; i < right; i++) {
        arr[i] = temp[i];
    }
}

下面画图理解递归是怎么操作的。
归并排序

冒泡排序

1
2
3
4
5
6
7
8
9
10
11
public static void bubble_sort(int[] arr,int right) {//每一轮把最大的一个数沉下去，下一轮就可以不用比较前一轮最后一个数
    for (int i = 1; i < right; i++) {//这个是从1开始
        for (int j = 1; j < right - i + 1; j++) {//不用再比较前一轮的最后一个数，size-i+1
            if (arr[j] < arr[j - 1]) {//因为和前一个比较，所以一开始的i起始位置是1
                int temp = arr[j];
                arr[j] = arr[j - 1];
                arr[j - 1] = temp;
            }
        }
    }
}

215 数组中的第K个最大元素 medium

这个题结合1738来看。思路：寻找第K个大的元素，可以用快速排序法，快速排序就是每次选择一个枢轴元素，然后比他小的在左边，比他大的在右边，最终可以确定枢轴元素的最终位置。对比这个位置和第K大的位置，如果比这个位置小，就在左边递归，反之右边递归。需要注意一个点，就是选择枢轴元素要随机选，不然会遇到极端案例，导致时间复杂度高。当然本题实际执行只考虑了比枢轴元素大的数以及把大的元素放在左边，是为了符合题目第k大的元素，注意本题解法也是一开始把枢轴元素放在最右边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
//Math.random()*(n-m)+m，生成大于等于m小于n的随机数
class Solution {
    public int findKthLargest(int[] nums, int k) {
        return quickSelect(nums, 0, k - 1, nums.length - 1);//第k大的位置也就是数组中k-1的位置
    }

    private int quickSelect(int[] arr, int left, int kth, int right) {
        int curPartition = partition(arr, left, right);
        if (curPartition == kth) {
            return arr[curPartition];
        } else if (curPartition < kth) {
            return quickSelect(arr, curPartition + 1, kth, right);
        } else {
            return quickSelect(arr, left, kth, curPartition - 1);
        }
    }

    private int partition(int[] arr, int left, int right) {
        int pivotIndex = left + (int)(Math.random() * (right - left + 1));//生成大于等于left小于等于right的随机数
        swap(arr, pivotIndex, right);//先把随机抽中的数与最右边的数交换。
        int index = left - 1;//把index初始化，一开始应该是-1。
        for (int i = left; i < right; i++) {//在区间范围内寻找
            if (arr[i] >= arr[right]) {//因为这个题说找最大的第k个数，所以只需要关注比这个枢轴元素大的数
                index += 1;//因为index一开始是-1
                swap(arr, index, i);//出现大于枢轴元素的数，就从左到右开始放。
            }
        }
        index += 1;//index加1，是为了下一步操作，把枢轴元素放到正确的位置
        swap(arr, index, right);//结束这个步骤，枢轴元素左边都是大于它的数，右边都是小于它的数
        return index;//返回随机抽中枢轴元素的位置
    }

    private void swap(int[] arr, int l, int r) {
        int temp = arr[l];
        arr[l] = arr[r];
        arr[r] = temp;
    }
}

/*写法2，自我感觉这种写法更好看
    private int partition(int[] arr, int left, int right) {
        int pivotIndex = left + (int)(Math.random() * (right - left + 1));
        swap(arr, pivotIndex, right);
        int index = left;//这里改变了
        for (int i = left; i < right; i++) {
            if (arr[i] >= arr[right]) {
                swap(arr, index, i);
                index += 1;//这里改变了
            }
        }
        //这里删除了
        swap(arr, index, right);
        return index;
    }
*/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//这个版本就是我们平时理解的快速排序。但是这个版本每次跑起来的速度和占用内存都不如上面那个好。
class Solution {
    public int findKthLargest(int[] nums, int k) {
        return quickSelect(nums, 0, k - 1, nums.length - 1);//第k大的位置也就是数组中k-1的位置
    }

    private int quickSelect(int[] arr, int left, int kth, int right) {
        int curPartition = partition(arr, left, right);
        if (curPartition == kth) {
            return arr[curPartition];
        } else if (curPartition < kth) {
            return quickSelect(arr, curPartition + 1, kth, right);
        } else {
            return quickSelect(arr, left, kth, curPartition - 1);
        }
    }

    private int partition(int[] nums, int left, int right) {
        int pivotIndex = left + (int)(Math.random() * (right - left + 1));//生成大于等于left小于等于right的随机数
        swap(nums, pivotIndex, left);//先把随机抽中的数与最右边的数交换。
        int first = left, last = right, key = nums[first];//注意这里是last = right ，而不是right-1，因为上面已经处理好边界是lenght-1
        while (first < last) {
            while (first < last && nums[last] <= key) {//这里是从右边扫描，小于的不管
                --last;
            }
            nums[first] = nums[last];//大于的就把这个数放到前面，这样可以符合题目第K大的条件
            while (first < last && nums[first] >= key) {
                ++first;
            }
            nums[last] = nums[first];
        }
        nums[first] = key;
        return first;}

    private void swap(int[] arr, int l, int r) {
        int temp = arr[l];
        arr[l] = arr[r];
        arr[r] = temp;
    }
}

347 前K个高频元素(桶排序) medium

首先用hash来创建一个key，value(频率)对应。然后再创建一个list，把相同频率的放在一个位置。最后从后往前面取出前k个来。也就是桶的思想。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/*
知识点
1.LinkedHashMap继承于HashMap,是基于HashMap和双向链表实现的
2.HashMap无序，LinkedHashMap有序，分为插入顺序和访问顺序
3.访问顺序操作的时候，put和get操作已存在的Entry时，都会把Entry移动到双向链表的表尾(也就是先删除再插入)
4.LinkedHashMap存取数据，还是跟HashMap一样使用Entry的方式，双向链表只是为了保证顺序
5.LinkenHashMap线程是不安全的
部分操作：
LinkedHashMap<Integer,Integer> map = new LinkedHashMap<>();//创建map
map.put(key,value)//存入key和value
map.get(key)//取出value
map.keySet()//打印的话是输出key的顺序
map.getOrDefault(Object key, V defaultValue)方法的作用是：当Map集合中有这个key时，就使用这个key值；如果没有就使用默认值defaultValue。

1.数组也就是Array（[]）：最高效；但是其容量固定且无法动态改变；使用时候 new和不new没有区别
2.ArrayList：容量可动态增长；但牺牲效率；详细见https://www.runoob.com/java/java-arraylist.html
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        LinkedHashMap<Integer,Integer> map = new LinkedHashMap<>();//以key,value来保存，本题key就是数字本身，value就是频率
        for (int i = 0; i < nums.length; i++) {//创建一个map来对应数字和频率
            if (map.containsKey(nums[i])) {//如果map中的key存在value
                map.put(nums[i], map.get(nums[i]) + 1);//注意不是map.get(nums[i] + 1)。从第二次开始就在基础频率上增加1
            } else {
                map.put(nums[i],1);//第一次大家都是空的，直接走这一步创建频率为1。
            }
        }
        List<Integer>[] ans=new List[nums.length + 1];//这个处理方式比较随意，会出现很多的null，至于多加1，举个例子把。[2,2]。这个2的频率是2。然后代码下面取的时候是ans[2(频率)]，但是我们知道下标如果是用length的话只有0,1。所以这个基础上加1。
        for(int num: map.keySet()){//把map中的key依次按顺序处理
            int i=map.get(num);//取出这个Key对应的value(频率)
            if(ans[i]==null){
                ans[i]=new ArrayList<>();//初始化，ans一开始本来就是空的嘛
            }
            ans[i].add(num);//同频率的key添加到同一个位置的ans中
        }
        int res[] = new int[k];//设置一个数组，长度为k
        int count = 0;//计数器
        for (int i = ans.length - 1; i >= 0 && count <k; i--) {//注意这里是ans.length，而不是nums.length。从后往前面操作，因为题目说是频率的前k个
            if (ans[i] != null) {//对ans中有数字的操作
                for (int j = 0; j < ans[i].size(); j++) {//然后取出这个位置中的ans
                    if (count < k) {
                        res[count++] = ans[i].get(j);//题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的.也就是如果题目要求k是2。但是频率最高的同时有3个数，这个是不成立的，也就不存在这个样例。所以每放进一个数，count就要增加1.
                    } else break;
                }
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
//这个解法稍微改了一点点，可以避免在生成bucket是时候浪费空间，能省一点是一点，但是实际测试的时候大家好像差不多，可能没有出现极端情况。
class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        LinkedHashMap<Integer,Integer> map = new LinkedHashMap<>();
        int frequency = 0;//频率计算
        for (int i = 0; i < nums.length; i++) {
            if (map.containsKey(nums[i])) {
                map.put(nums[i], map.get(nums[i]) + 1);
                frequency = Math.max(map.get(nums[i]),frequency);//找到最高频率
            } else {
                map.put(nums[i],1);
                frequency = Math.max(map.get(nums[i]),frequency);//找到最高频率
            }
        }
        List<Integer>[] ans=new List[frequency + 1];//长度只需要频率+1.这样可以避免上面的解法，省空间！！！
        for(int num: map.keySet()){
            int i=map.get(num);
            if(ans[i]==null){
                ans[i]=new ArrayList<>();
            }
            ans[i].add(num);
        }
        int res[] = new int[k];
        int count = 0;//计数器
        for (int i = ans.length - 1; i >= 0 && count <k; i--) {
            if (ans[i] != null) {//对ans中有数字的操作
                for (int j = 0; j < ans[i].size(); j++) {
                    if (count < k) {
                        res[count++] = ans[i].get(j);
                    } else break;
                }
            }
        }
        return res;
    }
}

451 根据字符出现频率排序(桶排序) medium

这个题主要和上一题对比的话，我觉得主要是一些语法上，比如对字符处理和上一题对数字的处理是不太一样的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public String frequencySort(String s) {
        Map<Character,Integer> map = new HashMap<Character,Integer>();
        int maxfreq = 0;//找出最高的频率
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            int frequency = map.getOrDefault(c, 0) + 1;//有就在频率的基础上加1，没有就默认0。
            map.put(c, frequency);//放入hash中
            maxfreq = Math.max(maxfreq, frequency);//找到频率最大值
        }
        StringBuffer[] buckets = new StringBuffer[maxfreq + 1];
         for (int i = 0; i <= maxfreq; i++) {
            buckets[i] = new StringBuffer();
        }
        //Map.entrySet() 这个方法返回的是一个Set<Map.Entry<K,V>>,Map.Entry里有相应的getKey和getValue方法
        for (Map.Entry<Character, Integer> entry : map.entrySet()) {//这个写法和上一题的不同之处。上一题都是整数，比较好处理。这个是字符，这样处理比较方便。
            char c = entry.getKey();//注意是getkey
            int frequency = entry.getValue();//注意是getvalue
            buckets[frequency].append(c); 
        }
        StringBuffer sb =new StringBuffer();
        for (int i = maxfreq; i > 0; i--) {
            StringBuffer bucket = buckets[i];
            for (int j = 0; j < bucket.length(); j++) {
                for (int k = 0; k < i; k++) {
                    sb.append(bucket.charAt(j));
                }
            }             
        }
        return sb.toString();
    }
}

75 颜色分类 medium

直接插入排序，但是貌似速度和内存都不占优势？

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public void sortColors(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            for (int j = i; j > 0 && nums[j] < nums[j-1]; j--) {
                int temp = nums[j];
                nums[j] = nums[j - 1];
                nums[j - 1] = temp;
            }
        }
    }
}

一切皆可搜索

695 岛屿的最大面积(DFS) medium

思路是深度优先遍历，分为主函数和辅助函数，主函数就是遍历每个点的位置，辅助函数就是dfs，设置好不满足的条件，满足条件的继续搜索。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int ans = 0;//最大数量初始化为0
        for (int i = 0; i < grid.length; i++) {//表示一共有多少行（也就是每列的长度，可以理解为Y，注意就是YYYYY）
            for (int j = 0; j < grid[0].length; j++) { //表示一共有多少列（也就是每行的长度，可以理解为X，注意就是XXXXX）
                ans = Math.max(ans, dfs(grid, i, j));//比较目前的岛屿是否最大，若不是，就替换为最大岛屿
            }
        }
    return ans;
    }
    public int dfs(int[][] grid, int cur_i, int cur_j) {
        //这个非常重要，是深度优先搜索的不满足条件。有超过边界的(i和j小于0；i等于列长度，j等于行长度，注意数组的开始位置是0哦；还有当前是海洋，也就是不是陆地的地方就不搜索)
        if (cur_i < 0 || cur_j < 0 || cur_i == grid.length || cur_j == grid[0].length || grid[cur_i][cur_j] != 1) {
            return 0;
        }
        grid[cur_i][cur_j] = 0;//当上面的条件都跳过了，也就是我们找到了一个陆地，这时候把他置为0，表示我们已经搜索过这个陆地了，然后开始上下左右搜索，不然应该会死循环。
        //这样可以组成 （0,1）（1,0）（-1,0）（0,-1）四种情况。
        int[] index_i = {0, 0, 1, -1};
        int[] index_j = {1, -1, 0, 0};
        int ans = 1;//陆地的数量初始为1
        for (int index = 0; index < 4; index++) {//遍历4次，走4个方向
            int next_inedx_i = cur_i + index_i[index];
            int next_inedx_j = cur_j + index_j[index];
            ans += dfs(grid, next_inedx_i, next_inedx_j);//把连起来的陆地加起来 
        }
    return ans;
    }
}
/*对于二维数组解释下长度问题
grid.length = 8 (8个一维数组，表示有多少行，也可以表示为每列的长度)
grid[0].length = 13（1个数组中有13个数，表示有多少列，也可以表示为每行的长度）
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
*/

547 省份数量(DFS) medium

做这个题的时候陷入到上一题的思维了，做题还是太少了！本题中有多少个二维数组中有多少个一维数组就代表多少个城市，每个一维数组里面的位置代表本城市(也就是i和j相同)或者其他城市(i和j不一样)，位置上为1代表有连接，也就是大家最后是属于一个省份的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
/*
思路：设置一个visit数组来表示访问过的城市。
访问第一个点，因为自己本身都是有1的，把visit[0]置为1(表示这个城市已经被访问过了)，这时候就开始深度优先搜索与这个城市相连的城市，然后依次类推，一直没有找到为止，这样就算完成了一个省份的搜索。开始执行下一个visit为0的城市访问。
*/

class Solution {
    public int findCircleNum(int[][] isConnected) {
        int citys = isConnected.length;//表示一共有多少个
        boolean[] visited = new boolean[citys];//全部城市访问都置为0
        int sum = 0;//省份数量初始为0
        for (int i = 0; i < citys; i++) {//开始搜索啦
            if(!visited[i]) {//只针对没有被访问的城市进行搜索
                dfs(isConnected, visited, citys, i);
                sum++;//上面全部搜索完，就相当于找到一个省份
            }
        }
    return sum;
}
    public void dfs(int[][] isConnected,boolean[] visited, int citys, int i) {
        for (int j = 0; j < citys; j++) {//i是固定的，然后逐个位置搜索看是否有1
            if (!visited[j] && isConnected[i][j] == 1) {//满足条件是位置上为1，已经这个城市没有被搜索过
                visited[j] = true;//满足了上面条件，记得把这个城市置为1，表示已经搜索过了
                dfs(isConnected, visited, citys, j);//开始搜索与i相连的城市，注意这里最后是jjjj。
                //所以，只要说一个城市被搜索过了，这个城市所有的连接情况我们都找到了，也就是他们是属于一个省份的。
            }
        }
    }
}

!417 太平洋大西洋水流问题(DFS) medium

一开始看了半天例子，以为那几点是形成河流的样子。ok，现在说下题目意思，是找出所有的点，这个点可以流向太平洋，也能流向大西洋 ，所以看例子的时候，单独看每一个点，然后需要自己画出流动方向。
!代表我在Leetcode上写题解了，哈哈。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
    public List<List<Integer>> pacificAtlantic(int[][] heights) {
        int n = heights.length;//二维数组的行数
        int m = heights[0].length;//二维数据的列数
        boolean[][] can_reach_p = new boolean[n][m];//初始化可以到达太平洋的数组
        boolean[][] can_reach_a = new boolean[n][m];//初试化可以到达大西洋的数组
        for (int i = 0; i < n; i++) {
            dfs(heights, i, 0, can_reach_p);//搜索左列，也就是靠近太平洋
            dfs(heights, i, m - 1, can_reach_a);//搜索右列，也就是靠近大西洋
        }
        for (int j = 0; j < m; j++) {
            dfs(heights, 0, j, can_reach_p);//搜索上列，也就是靠近太平洋
            dfs(heights, n - 1, j, can_reach_a);//搜索下列，也就是靠近大西洋
        }
        List<List<Integer>> res = new ArrayList<>();//初始化一个list来保存符合条件的坐标
        //全部坐标进行判断
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (can_reach_a[i][j] && can_reach_p[i][j]) {//判断这个坐标是否同时流向太平洋和大西洋
                    res.add(List.of(i, j));
                }
            }
        }
        return res;
     
    }
    public void dfs(int[][] heights, int i, int j, boolean[][] can_reach) {
        if (can_reach[i][j] == true) {//如果这个坐标是1，就说明人家早就满足条件了，不需要再进行深度搜索了
            return;
        }
        can_reach[i][j] = true;//首先把这个坐标给置为1，代表可以达到海洋
        //因为坐标只能进行上下左右移动，也就是(0,1),(0,-1),(1,0),(-1,0)。所以设置成下面这种格式
        int[] index_i = {0, 0, 1, -1};
        int[] index_j = {1, -1, 0, 0};
        for (int index = 0; index < 4; index++) {//上下左右4次坐标都要判断
            int next_index_i = i + index_i[index];//设置下一个坐标的i
            int next_index_j = j + index_j[index];//设置下一个坐标的j
            //需要满足下面的条件才能进行深度搜索，不能超过边界，还有下一个坐标要比原来坐标大或者相等。
            if (next_index_i >= 0 && next_index_i < heights.length && next_index_j >= 0 && next_index_j < heights[0].length && heights[i][j] <= heights[next_index_i][next_index_j]) {
                            dfs(heights, next_index_i, next_index_j, can_reach);
            }

        }
    } 
}

46 全排列(回溯法) medium

DFS基本操作：[修改当前节点状态]->[递归子节点状态]。回溯法：[修改当前节点状态]->[递归子节点状态]->[回改当前节点状态]。回溯法是优先搜索的一种特殊状态。一般在排列，组合，选择类问题使用回溯法，这次官方那个视频讲解不错，本题就是按照这个思路来。

1
2
3
4
知识点
注意后面的new的写法
栈：Deque<Integer> path = new ArrayDeque<>();
list里面还有一个list： List<List<Integer>> res = new ArrayList<>();
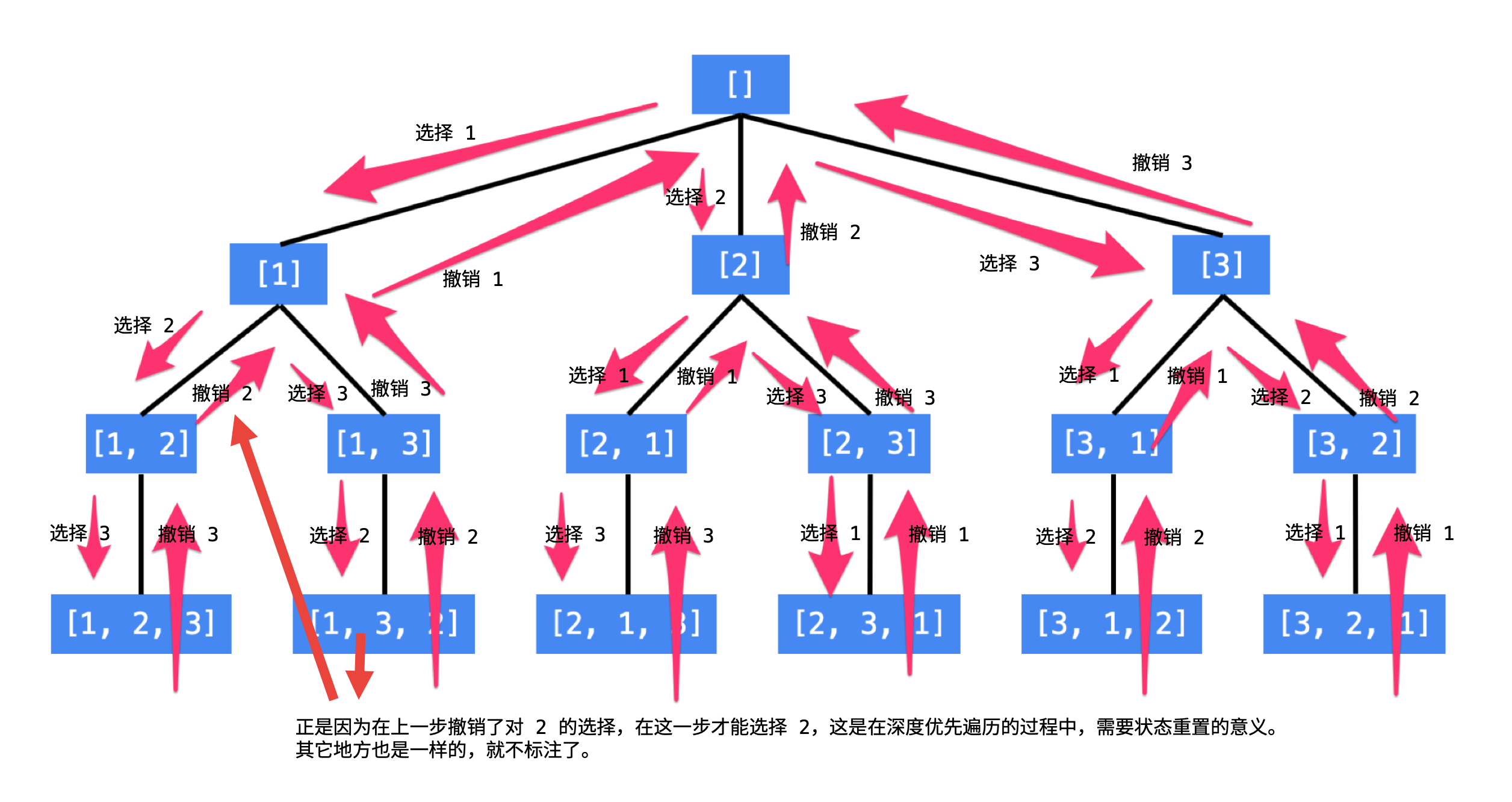
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    //状态变量：depth，path，used
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        int len = nums.length;
        boolean[] used = new boolean[len];
        if (len == 0) {
            //System.out.println("  res:"+res);
            return res;
        }
        Deque<Integer> path = new ArrayDeque<>();//栈的应用
        dfs(nums, len, 0, path, used, res);
        return res;
    }
    public void dfs(int[] nums,int len, int depth, Deque<Integer> path, boolean[] used, List<List<Integer>> res) {
        if (depth == len) {
            /*下面这一句超级超级重要，如果改成res.add(path)。最后输出是[[],[],[],[],[],[]]。
            为什么会这样呢？
            变量 path 所指向的列表 在深度优先遍历的过程中只有一份 ，深度优先遍历完成以后，回到了根结点，成为空列表。
            在 Java 中，参数传递是 值传递，对象类型变量在传参的过程中，复制的是变量的地址。这些地址被添加到 res 变量，但实际上指向的是同一块内存地址，因此我们会看到 6 个空的列表对象。解决的方法很简单，在 res.add(path); 这里做一次拷贝即可。
            */
            res.add(new ArrayList(path));
            return;
        }
        for (int i = 0; i < len; i++) {
            if (used[i] == true) { //如果发现某个位置已经用了，就跳过
                continue;
            }
            path.addLast(nums[i]);//栈的添加操作
            used[i] = true;//然后把这个位置设置为已经用了
            //System.out.println("  递归之前 => " + path+ "  i: " + i + "  used：  " + Arrays.toString(used));
            dfs(nums, len, depth + 1, path, used, res);//进行递归操作
            used[i] = false;//回改节点状态
            path.removeLast();//回改节点状态，也就是栈的移除操作。
            //System.out.println("递归之后 => " + path+ "  i: " + i+ "  used：  " + Arrays.toString(used));
        } 
    }
}

下面引用一张别人图片来描述这个算法流程。
46题全排列1
然后下面这种图片是一些代码流程细节上的理解，注意当代码运行到dfs里面的时候，会回到for，然后for是重新为0的。
46题全排列2

77 组合(回溯法) medium

注意排列是不重复的，组合是的话[1,2]和[2,1]是一个情况，还有不能对自己组合哦。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
//这个写法受到了上一个的影响，不够简洁，实际上完全没有必要用到used，注意有个地方不一样！！！！在唯一一个注释里面！！！
    public List<List<Integer>> combine(int n, int k) {
        boolean[] used =new boolean[n];
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }
        Deque<Integer> path = new ArrayDeque<>();
        int[] nums = new int[n];
        for(int i = 0; i < n; i++) {
            nums[i] = i + 1;
        }
        dfs(nums, n, k, 0, path, used, res);
        return res;
    }
    public void dfs(int[] nums, int n, int k, int begin, Deque<Integer> path, boolean[] used, List<List<Integer>> res) {
        if (path.size() == k) {
            res.add(new ArrayList(path));
            return;
        }
        for (int i = begin; i < n; i++ ) {
            if (used[i] == true) {
                continue;
            }
            used[i] = true;
            path.addLast(nums[i]);
            dfs(nums, n, k, i + 1, path, used, res);//这里不是begin + 1而是i + 1，不然会有重复的组合，因为我们这个题是组合，组合，组合，不是排列！！！！ 比较一下上一题是depth的含义。
            used[i] = false;
            path.removeLast();
        }
    }
}
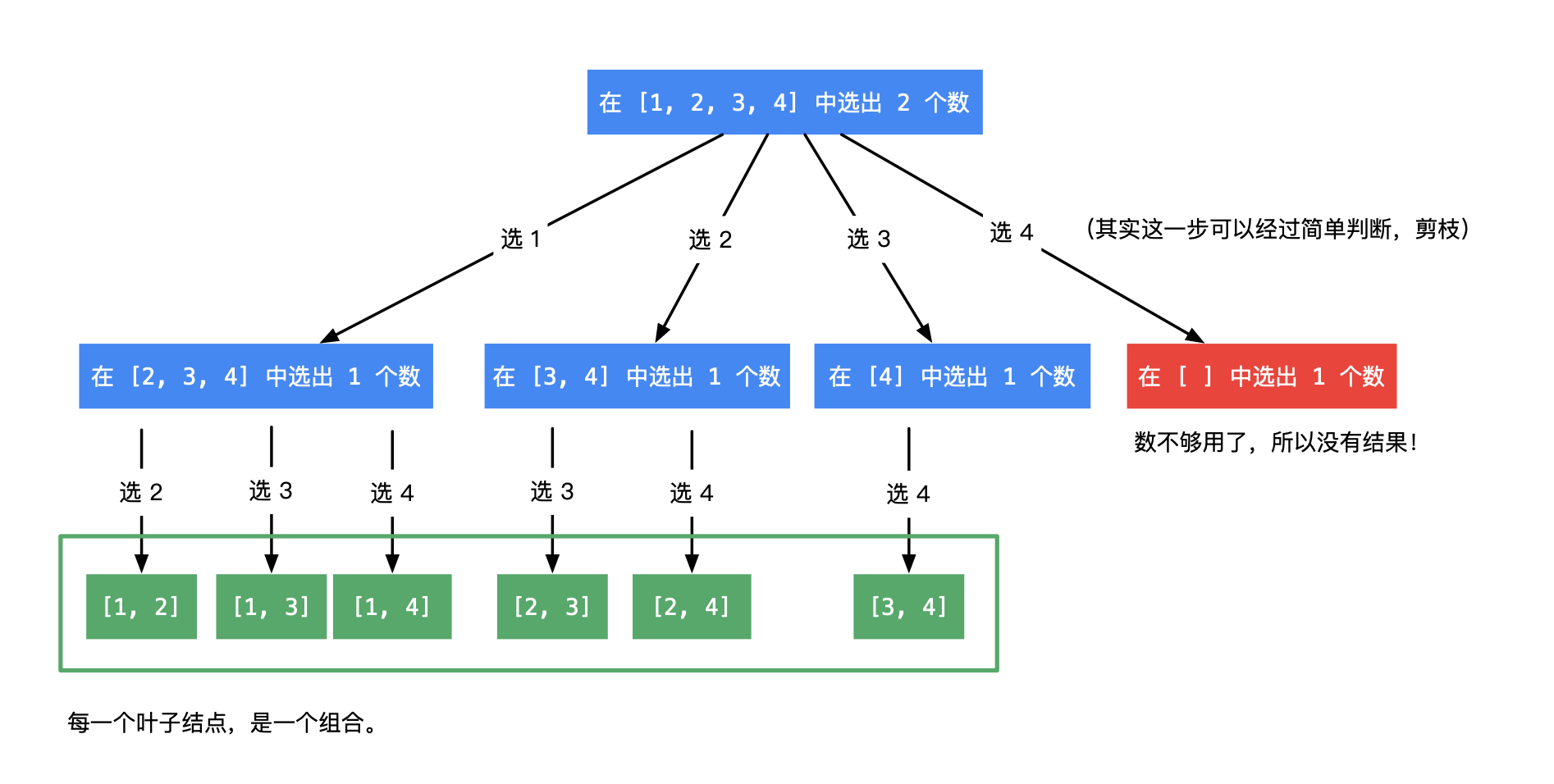
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//大佬的简洁解法，还有一个解法会更加省时间，但是不好想，也就是剪枝。具体还是看下面的链接。
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;

public class Solution {

    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }
        // 从 1 开始是题目的设定
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, k, 1, path, res);
        return res;
    }

    private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) {
        // 递归终止条件是：path 的长度等于 k
        if (path.size() == k) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 遍历可能的搜索起点
        for (int i = begin; i <= n; i++) {
            // 向路径变量里添加一个数
            path.addLast(i);
            // 下一轮搜索，设置的搜索起点要加 1，因为组合数理不允许出现重复的元素
            dfs(n, k, i + 1, path, res);
            // 重点理解这里：深度优先遍历有回头的过程，因此递归之前做了什么，递归之后需要做相同操作的逆向操作
            path.removeLast();
        }
    }
}

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/combinations/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-ma-/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

用下大佬的图理解这个题
77组合
总结：77题和46题回溯法，一定要先画图！！！看看他们不一样的点，dfs判断加入path的条件，以及在for循环中dfs的写法，这些都是值得注意的。

79 单词搜索(回溯法) medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class Solution {
    public boolean exist(char[][] board, String word) {
        int m = board.length;
        int n = board[0].length;
        boolean[][] visited = new boolean[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                boolean flag = backtracking(i, j, board, word, visited, 0);
                if (flag) {
                    return true;
                }
            }
        }
    return false;
    }
        public boolean backtracking(int i, int j, char[][] board, String word, boolean[][] visited, int pos) {
        if (board[i][j] != word.charAt(pos) || visited[i][j] ==true) {//这两个if判断不能对调,因为首先你得判断配对是不是一样的字符，然后才判断他是不是最后一个字符的位置
            return false;
        } else if (pos == word.length() - 1) {
            return true;
        }
        visited[i][j] = true;
        int[] index_i = {0, 0, 1, -1};
        int[] index_j = {1, -1, 0, 0};
        boolean result = false;
        for (int index = 0; index < 4; index++) {
            int next_index_i = i + index_i[index];//设置下一个坐标的i
            int next_index_j = j + index_j[index];//设置下一个坐标的j
            if (next_index_i >= 0 && next_index_i < board.length && next_index_j >= 0 &&  next_index_j < board[0].length) {
                boolean flag = backtracking(next_index_i, next_index_j, board, word, visited, pos + 1);
                if (flag) {
                    result = true;
                    break;
                }   
            }
        }
        visited[i][j] = false;
        return result;
        }
}
/*还可以改成这样，不太喜欢这种写法。
    public boolean backtracking(int i, int j, char[][] board, String word, boolean[][] visited, int pos) {
        //这里改了。
        if (board[i][j] != word.charAt(pos)) {
            return false;
        } else if (pos == word.length() - 1) {
            return true;
        } 
        visited[i][j] = true;
        int[] index_i = {0, 0, 1, -1};
        int[] index_j = {1, -1, 0, 0};
        boolean result = false;
        for (int index = 0; index < 4; index++) {
            int next_index_i = i + index_i[index];//设置下一个坐标的i
            int next_index_j = j + index_j[index];//设置下一个坐标的j
            if (next_index_i >= 0 && next_index_i < board.length && next_index_j >= 0 &&  next_index_j < board[0].length) {
                if (visited[next_index_i][next_index_j] == false) {//这里改了，注意这里是next的判断
                    boolean flag = backtracking(next_index_i, next_index_j, board, word, visited, pos + 1);
                    if (flag) {
                        result = true;
                        break;
                    }
                }
            }
        }
        visited[i][j] = false;
        return result;
        }
*/

下面这个是按照书上思路改写的，但是错误，先放着，未来会修改(已修改，看下面)，初步判断是因为find不是全局变量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
//！！！！这是错误的，错误的！！！正确写法在下一个代码中
    public boolean exist(char[][] board, String word) {
        int m = board.length;
        int n = board[0].length;
        boolean[][] visited = new boolean[m][n];
        boolean find = false;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                backtracking(i, j, board, word, find, visited, 0);
            }
        }
    return find;
    }
    public void backtracking(int i, int j, char[][] board, String word, boolean find, boolean[][] visited, int pos) {
        if (i < 0 || i >= board.length || j < 0 ||  j >= board[0].length) {
            return;
        }
        if (board[i][j] != word.charAt(pos) || visited[i][j] || find) {
            return;
        }
        if (pos == word.length() - 1) {
            find = true;
            return;
        }
        visited[i][j] = true;
        backtracking(i + 1, j, board, word, find, visited, pos + 1);
        backtracking(i - 1, j, board, word, find, visited, pos + 1);
        backtracking(i, j + 1, board, word, find, visited, pos + 1);
        backtracking(i, j - 1, board, word, find, visited, pos + 1);
        visited[i][j] = false;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//正确写法
class Solution {
    private boolean find = false;//设为全局变量
    public boolean exist(char[][] board, String word) {
        if(board == null) return false;
        boolean[][] visited = new boolean[board.length][board[0].length];
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                backTracking(i, j, board, word, visited, 0);//不用传find
            }
        }
        return find;
    }

    public void backTracking(int i, int j, char[][] board, String word, boolean[][] visited, int pos) {
        if(i < 0 || i >= board.length || j < 0 || j >= board[0].length || visited[i][j] || board[i][j] != word.charAt(pos) || find) return;
        if(pos == word.length() - 1) {
            find = true;
            return;
        }
        visited[i][j] = true;
        backTracking(i - 1, j, board, word, visited, pos + 1);
        backTracking(i + 1, j, board, word, visited, pos + 1);
        backTracking(i, j - 1, board, word, visited, pos + 1);
        backTracking(i, j + 1, board, word, visited, pos + 1);
        visited[i][j] = false;
    }
}

51 N皇后(回溯法) hard

久闻的经典题！题目要求就是任何两个皇后都不能在同一行、同一列以及同一条斜线上。思考：斜线怎么判断？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
//这是别人用java改写labuladong的C++版本，感觉非常好理解。
class Solution {
    List<List<String>> res = new ArrayList<>();//这里是全局哦
    public List<List<String>> solveNQueens(int n) {
        char[][] board = new char[n][n];
        //初始化棋盘
        for (char[] c : board) {
            Arrays.fill(c, '.');
        }
        backtracking(board, 0);
        return res;
    }
    public void backtracking(char[][] board, int row) {
        //每一行都成功放置好了皇后，注意这里不是board.length - 1，我的理解是，首先你row进来是检查能不能放，所以最后全部放好后，row会+1,，这时候才判断已经全部能放。
        if (row == board.length) {
            res.add(charToList(board));
            return;
        }
        int n = board[row].length;//其实有没有row都一样，都是N*N棋盘。
        //对列进行遍历
        for (int col = 0; col < n; col++) {
            if (!isValid(board, row, col)) {//判断能不能放皇后，不能放就跳过
                continue;
            }
            board[row][col] = 'Q';//能放就置为Q
            backtracking(board, row + 1);//对下一行进行操作
            board[row][col] = '.';//回溯法关键，也就是恢复原来标记
        }
    }
    public boolean isValid(char[][] board, int row, int col) {
        int n = board.length;
        //判断列是否能放皇后
        for (int i = 0; i < n; i++) {
            if (board[i][col] == 'Q') {
                return false;
            }
        }
        //判断右上方有没有皇后冲突
        for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {//先跳到上一行，列也要加一行，依次类推，注意边界！
            if (board[i][j] == 'Q') {
                return false;
            }
        }
        //判断左上方有没有皇后冲突
        for (int i = row - 1, j = col - 1; i >= 0 && j >=0; i--, j--) {//先跳到上一行，列也要减一行，依次类推，注意边界！
            if (board[i][j] == 'Q') {
                return false;
            }
        }
        return true;
        //这里为什么不进行左下方和右下方进行判断？因为是一行行进行放，这时候左下和右下必定没有呀
    }
    public List charToList(char[][] board) {
        List<String> list = new ArrayList<>();
        for (char[] c : board) {
            list.add(String.copyValueOf(c));
        }
        return list;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
本题有很多需要学习的写法
1.for (char[] c : board) {
    System.out.print("1");
  }
本句输出是1111，也就是说，对于Arrays.fill(c, '.')每次操作，都是[., ., ., .]，一次性把每行的4个位置都填充上，然后一共操作4次而不是16次。

2.Arrays.fill(c, '.');//初始化棋盘这里
for (int i = 0;i<n;i++){
    System.out.print(Arrays.toString(board[i]));
}
输出结果是：
[., ., ., .][., ., ., .][., ., ., .][., ., ., .]

3.for (char[] c : board) {
            list.add(String.copyValueOf(c));
}
首先为什么要这么操作，因为输入是一个二维数组来的，最后的输出要符合题目输出，把每一个一维数组加到list中！
这一段的操作是这样看，首先是输入一个已经摆放好皇后的棋盘
String.copyValueOf是返回字符串
然后char c是提取每一行出来，比如第一行.Q..然后add到list中，最后扫描完所有行list是这样[.Q.., ...Q, Q..., ..Q.]，然后再res.add进去。

934 最短的桥(DFS+BFS) medium

一般广度优先遍历用于求最短路径或者可达性问题。本题实际上就是求两个岛屿之间的最短距离，先任意找到一个岛，然后用广度优先搜索寻找和另外一个岛屿的最短距离。结合了书和该作者的想法。做完这个题其实还是有点不理解，因为首先是找到了第一个岛后就break掉了，那怎么知道其他岛与其他岛会不会有更小的距离呢？经过我的探索，终于知道了，因为题目样例中有且仅有两个岛！！！！！！不会出现第三个岛！！！！务必知道挨着的1是属于一个岛！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
有个地方需要注意，两个陆地挨着的属于一个岛。比如[[1,0,0],[1,0,0],[0,0,0]]这种情况是一个岛，当然了，这个用例是不能被输入的，因为必须要有两个岛。还有这个题返回的是必须翻转0的数目。
class Solution {
    public int shortestBridge(int[][] grid) {
        int[][] direction = new int[][]{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};//四个方向坐标
        int n = grid.length;
        int m = grid[0].length;
        int ans = -1;//初始化距离，这里为什么要设置-1而不是0，因为一进入下面的while后首先是搜索以自己为目标的四周，所以第一次进入while，先ans++，这样就初始化了为0，然后再从我自己扩散出去，而且循环里面是找到了下一个陆地直接返回ans，没有进行加加，一开始提前了ans++。
        boolean flag = false;
        Deque<int []> point = new ArrayDeque<>();//队列记录坐标
        //dfs寻找第一个岛，并把这个岛全部标记为2，注意想象一下周围一圈都是1，表达是一个岛，会把这一圈的1都标记为2
        for (int i = 0; i < n; i++) {
            if (flag == true) break;
            for (int j = 0; j < m ; j++) {
                if (grid[i][j] == 1) {
                    dfs(grid, point, i, j); 
                    flag = true;//代表找到了岛
                    break;
                }
            }
        }
        //进行广度搜索，看多少层能到下一个陆地
        while (!point.isEmpty()) {//point不为空
            int size = point.size();
            ans++;//每扩散一次，距离加1
            for (int i = 0; i < size; i++) {//依次对标记过为2的岛进行操作
                //System.out.print("hello  "+ ans+"   "+"  ");
                int[] node = point.poll();//取出队列中第一个岛的坐标，并删除队列中该坐标
                for (int j = 0; j < 4; j++) {//上下左右寻找
                    int next_x = node[0] + direction[j][0];
                    int next_y = node[1] + direction[j][1];
                    if(next_x < 0 || next_x >= grid.length || next_y < 0 || next_y >= grid[0].length || grid[next_x][next_y] == 2) {//判断：不能超边界以及不能是访问过的陆地
                        continue;
                    }
                    if (grid[next_x][next_y] == 1) {//找到下一个岛
                        return ans;
                    }
                    grid[next_x][next_y] = 2;//走过的地方要标记为2(这些地方可能是水哦)
                    point.add(new int[]{next_x, next_y});//把这些坐标都记录起来
                }
            }
        }
        return ans;
    }
    public void dfs(int[][] grid, Deque<int []> point, int i, int j) {
        if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == 2 || grid[i][j] != 1) {//边界判断以及走过的地方不搜索还有不是陆地的不搜索
            return;
        }
        grid[i][j] = 2;
        point.add(new int[]{i, j});
        dfs(grid, point, i - 1, j);
        dfs(grid, point, i + 1, j);
        dfs(grid, point, i, j - 1);
        dfs(grid, point, i, j + 1);

    }
}举个例子：
现在两个岛是这样的，就是一个L型和中间一块小岛
[[1,0,0,0,0],[1,0,0,0,0],[1,0,1,0,0],[1,0,0,0,0],[1,1,1,1,1]]
下面最左边的9和7代表队列中的元素个数，hello具体位置在上面代码看，表达进入for循环，hello右边是ans的大小，最右边是取出来的坐标。可以看到，先把L型岛坐标全部放进队列，然后一个个坐标取出来再再看四周(并且也把四周的点加入到队列)，第一轮发现是没有碰到陆地的，所以到了第二轮，第二轮是7因为L型右边的坐标围起来是7个，然后开始继续找，到了2,1坐标，可以知道右边一个位置是1，这时候已经找到了，返回ans。
9  hello  0     0 0
hello  0     1 0
hello  0     2 0
hello  0     3 0
hello  0     4 0
hello  0     4 1
hello  0     4 2
hello  0     4 3
hello  0     4 4
7  hello  1     0 1
hello  1     1 1
hello  1     2 1

126 单词接龙2(回溯+BFS) hard

单词只差一个字母的可以连接成节点，思考如何去判断只相差一个字母？回溯也就是深度优先搜索的一个应用，用于找出所有情况，BFS也就是找到最短路径，合起来就是找出所有的最短路径。这个题和上一个题差不多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
//官方的解答，学到就是我的🤓
class Solution {
    public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
        List<List<String>> res = new ArrayList<>();
        Set<String> dict = new HashSet<>(wordList);// 因为需要快速判断扩展出的单词是否在 wordList 里，因此需要将 wordList 存入哈希表，这里命名为「字典」
        if (!dict.contains(endWord)) {// 特殊用例判断
            return res;
        }
        dict.remove(beginWord);//把beginword在字典里删除掉

        // 第 1 步：广度优先遍历建图
        // 记录扩展出的单词是在第几次扩展的时候得到的，key：单词，value：在广度优先遍历的第几层
        Map<String, Integer> steps = new HashMap<>();
        steps.put(beginWord, 0);

        // 记录了单词是从哪些单词扩展而来，key：单词，value：单词列表，这些单词可以变换到 key ，它们是一对多关系
        Map<String, List<String>> from = new HashMap<>();
        int step = 1;
        boolean found = false;
        int wordlen = beginWord.length();//记录单词的长度，以便于对每个字符进行更换
        Queue<String> queue = new LinkedList<>();
        queue.offer(beginWord);//把开始的单词加进去

        while(!queue.isEmpty()) {//不为空就运行
            int size = queue.size();
            for (int i = 0; i < size; i++) {//对queue里面的单词依次操作
                String currword = queue.poll();//先取出queue第一个单词
                char[] chararray = currword.toCharArray();//将字符串转换为字符数组
                for (int j = 0; j < wordlen; j++) {//对每一个位置的字符进行操作
                    char origin = chararray[j];//先保存原来的字符，以便后面进行恢复
                    for (char c = 'a'; c <= 'z'; c++) {//每个位置都可以替换26次（包括原来的自己啦）
                        chararray[j] = c;//替换成果
                        String nextword = String.valueOf(chararray);//char数组转成字符串
                        if (steps.containsKey(nextword) && step == steps.get(nextword)) {//初步理解就是，如果大家都在同一个level的词变换，就进行操作添加这个词
                            //System.out.print("nextword is "+nextword);
                            //System.out.print("currword is "+currword);
                            from.get(nextword).add(currword);//如果有这个key的记录, 添加新值
                            //System.out.println("from is a  "+from);
                        }
                        if (!dict.contains(nextword)) {//dict中不存在这个单词就跳过
                            continue;
                        }

                        //下面这两句思考一下！！！！！
                        dict.remove(nextword);//如果从一个单词扩展出来的单词以前遍历过，距离一定更远，为了避免搜索到已经遍历到，且距离更远的单词，需要将它从 dict 中删除
                        queue.add(nextword); // 那么这一层扩展出的单词进入队列
                        // 记录 nextword 从 currWord 而来
                        from.putIfAbsent(nextword, new ArrayList<>());
                        from.get(nextword).add(currword);
                        // 记录 nextword 的 step
                        steps.put(nextword, step);
                        if (nextword.equals(endWord)) {//等于最后一个单词就把found设置为true
                            found = true;
                        }
                        //System.out.println("dict is "+dict);
                        //System.out.println("queue is "+queue);
                        //System.out.println("from is "+from);
                        //System.out.println("steps is "+steps);
                    }
                    chararray[j] = origin;//还原单词
                }
            }
            step++;//level加1
            if (found) {//找到就打断程序
                break;
            }
        }
        // 第 2 步：深度优先遍历找到所有解，从 endWord 恢复到 beginWord ，所以每次尝试操作 path 列表的头部
        if (found) {
            Deque<String> path = new ArrayDeque<>();
            path.add(endWord);
            backtracking(from, path ,beginWord ,endWord ,res);
        }
        return res;
    }
    //注意这个回溯反着来找，从尾巴一直寻找到最开始，就是根据from记录的信息来寻找
    public void backtracking(Map<String, List<String>> from, Deque<String> path, String beginWord, String cur, List<List<String>> res) {
        if (cur.equals(beginWord)) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (String preucrsor : from.get(cur)) {
            path.addFirst(preucrsor);
            backtracking(from, path, beginWord, preucrsor, res);
            path.removeFirst();
        }
    }
}
/*
老规矩，看不懂怎么运行就一步步打印出来
dict is [lot, log, dot, cog, dog]
queue is [hot]
from is {hot=[hit]}
steps is {hit=0, hot=1}

dict is [lot, log, cog, dog]
queue is [dot]
from is {dot=[hot], hot=[hit]}
steps is {hit=0, dot=2, hot=1}

dict is [log, cog, dog]
queue is [dot, lot]
from is {lot=[hot], dot=[hot], hot=[hit]}
steps is {lot=2, hit=0, dot=2, hot=1}

dict is [log, cog]
queue is [lot, dog]
from is {lot=[hot], dot=[hot], hot=[hit], dog=[dot]}
steps is {lot=2, hit=0, dot=2, hot=1, dog=3}

dict is [cog]
queue is [dog, log]
from is {lot=[hot], log=[lot], dot=[hot], hot=[hit], dog=[dot]}
steps is {lot=2, hit=0, log=3, dot=2, hot=1, dog=3}

dict is []
queue is [log, cog]
from is {lot=[hot], log=[lot], dot=[hot], cog=[dog], hot=[hit], dog=[dot]}
steps is {lot=2, hit=0, log=3, dot=2, cog=4, hot=1, dog=3}

//这个是第一个if语句中的输出，对于这个例子，一共才运行了一次，仔细观察cog这个值多了一个log
nextword is cog
curword is log
from is a  {lot=[hot], log=[lot], dot=[hot], cog=[dog, log], hot=[hit], dog=[dot]}
*/
1
2
3
4
5
6
7
8
map和hashmap区别?
queue和Deque区别?
add offer等操作区别?
contains和containskey区别?
put和putIfAbsent区别：put在放入数据时，如果放入数据的key已经存在与Map中，最后放入的数据会覆盖之前存在的数据，而putIfAbsent在放入数据时，如果存在重复的key，那么putIfAbsent不会放入值。
测试的时候发现下面两种写法都是可以的，可以百度下他们的不同。
Deque<String> path = new ArrayDeque<>();
Deque<String> path = new ArrayList<>();

130 被围绕的区域 medium

采用深度优先遍历递归，首先要理解就是只有被X包围的区域O才被替换，所以在边界的O是不能被替换的，延伸下去的话，和边界O相连的O也是不能够被替换的，所以这个题目的思想就是，从边界O下手，然后找到和这个边界O相连的O，然后把他们都替换成一个字符#，最后再做一次全局的遍历，把没被替换成O的换成X，把#恢复成O。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    public void solve(char[][] board) {
        if (board == null || board.length == 0) {
            return;
        }
        int n = board.length, m = board[0].length;
        for (int i = 0; i < n; i++) {
            for(int j = 0; j < m; j++) {
                boolean isEdge = i == 0 || i == n - 1 || j == 0 || j == m - 1;
                if (isEdge && board[i][j] == 'O') { //只需要从边界下手，其他地方不需要
                    dfs(board, i ,j);
                }
            }
          }
         for (int i = 0; i < n; i++) {  //都遍历完了，再全局遍历进行更换字符
             for (int j = 0; j < m; j++) {
                 if  (board[i][j] == 'O') {
                     board[i][j] = 'X';
                 }
                 if (board[i][j] == '#') {
                     board[i][j] = 'O';
                 }
             }
         }    
    }
    public void dfs(char [][]board, int i ,int j) { //深度优先遍历
        if (i < 0 || j < 0 || i >= board.length || j >= board[0].length || board[i][j] == 'X' || board[i][j] == '#') { //边界条件以及本来是X和#的不需要操作
            return;
        }
        board[i][j] = '#';
        dfs(board, i + 1, j);
        dfs(board, i - 1, j);
        dfs(board, i , j + 1);
        dfs(board, i , j - 1);
    }
}

257 二叉树的所有路径 easy

深度优先遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> paths = new ArrayList<String>();
        constructpath(root, "", paths);
        return paths;
    }
    public void constructpath(TreeNode root, String path, List<String> paths) {
        if (root != null) {
            StringBuffer temppath = new StringBuffer(path); //注意这里，每次递归都对变量path进行拷贝构造
            temppath.append(root.val);
            if (root.left == null && root.right == null) {  //到了叶子节点就代表结束了
                paths.add(temppath.toString());
            }
            else {
                temppath.append("->");
                constructpath(root.left, temppath.toString(), paths);
                constructpath(root.right, temppath.toString(), paths);
            }
        }    
    }
}
1
2
3
4
5
6
对于append和add的用法总结：
1.append
Java里只有StringBuffer和StringBuild才有append方法，Sting里是没有append方法的

2.add
List集合列表中添加元素

47 全排列2 medium

和46的区别是，这个题是有重复数字的，而且重复数字不是有序的，而是打乱的。官网的题解更简洁

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        int len = nums.length;
        boolean[] used = new boolean[len];
        if (len == 0) {
            return res;
        }
        Arrays.sort(nums); //区别1，首先要对数列进行排序
        Deque<Integer> path = new ArrayDeque<>();
        dfs(nums, len, 0, path, used, res);
        return res;
    }
    public void dfs(int[] nums, int len, int depth, Deque<Integer> path, boolean[] used, List<List<Integer>> res) {
        if (depth == len) {
            res.add(new ArrayList(path));
            return;
        }
        for (int i = 0; i < len; i++) {
            if (used[i] == true || (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false)) { //区别2，还要判断和前一个数是不是一样的，这里used[i - 1] == false不好理解，下面单独解释
                continue;
            }
            path.addLast(nums[i]);
            used[i] = true;
            dfs(nums, len, depth + 1, path, used, res);
            used[i] =  false;
            path.removeLast();
        }
    }
}
1
2
3
4
5
6
7
8
9
这个题首先要排序哦
i > 0 && nums[i] == nums[i - 1]这个很好理解，就是重复的数字不要再进行了，但是used[i - 1] == false这个其实是不好理解的，我在做的时候就在想为什么还要多加这个条件呢？。

来自网友1的解释（vis和上面used作用一样）：
加上 !vis[i - 1]来去重主要是通过限制一下两个相邻的重复数字的访问顺序
举个栗子，对于两个相同的数11，我们将其命名为1a1b, 1a表示第一个1，1b表示第二个1； 那么，不做去重的话，会有两种重复排列 1a1b, 1b1a， 我们只需要取其中任意一种排列； 为了达到这个目的，限制一下1a, 1b访问顺序即可。 比如我们只取1a1b那个排列的话，只有当visit nums[i-1]之后我们才去visit nums[i]， 也就是如果!visited[i-1]的话则continue

来自网友2的解释：
for循环保证了从数组中从前往后一个一个取值，再用if判断条件。所以nums[i - 1]一定比nums[i]先被取值和判断。如果nums[i - 1]被取值了，那vis[i - 1]会被置1，只有当递归再回退到这一层时再将它置0。每递归一层都是在寻找数组对应于递归深度位置的值，每一层里用for循环来寻找。所以当vis[i - 1] == 1时，说明nums[i - 1]和nums[i]分别属于两层递归中，也就是我们要用这两个数分别放在数组的两个位置，这时不需要去重。但是当vis[i - 1] == 0时，说明nums[i - 1]和nums[i]属于同一层递归中（只是for循环进入下一层循环），也就是我们要用这两个数放在数组中的同一个位置上，这就是我们要去重的情况。

40 组合总和 II medium

深度优先遍历，务必注意解集不能包含重复组合，每个数字在每个组合中只能使用一次，这个博主解释不错。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        if(len == 0) {
            return res;
        }
        Arrays.sort(candidates);//务必要排序
        Deque<Integer> path = new ArrayDeque<>(len);//用双端队列会更好操作，不加len也可以
        dfs(candidates, len, 0, target, path, res);
        return res;
    }
    private void dfs(int[] candidates, int len, int begin, int target, Deque<Integer> path, List<List<Integer>> res) {
        if(target == 0) {
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i = begin; i < len; i++) {
            if(target - candidates[i] < 0) {//如果减了小于0，就没必要进行了
                break;
            }
            if(i > begin && candidates[i] == candidates[i - 1]) {//同一层相同元素只考虑第一个，没有这个操作可能会导致结果集合一样，i>begin是精髓，可以看上面链接中的评论，有详细回答。
                continue;
            }
            path.addLast(candidates[i]);
            dfs(candidates, len, i + 1, target - candidates[i], path, res);
            path.removeLast();//深度遍历思想是继续往下探索如果没有就返回
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//Linklist写法
class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(candidates);
        LinkedList<Integer> path = new LinkedList<Integer>();//这里不同
        dfs(candidates, len, target, 0, res, path);
        return res;
    }
    private void dfs(int[] candidates, int len,int target, int begin, List<List<Integer>> res, LinkedList<Integer> path) {
        if(target == 0) {
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i = begin; i < len; i++) {
            if(target - candidates[i] < 0) {
                break;
            }
            if(i > begin && candidates[i] == candidates[i - 1]) {
                continue;
            }
            path.add(candidates[i]);//这里不同
            dfs(candidates, len, target - candidates[i], i + 1, res, path);
            path.removeLast();
        }
    }
}

37 解数独 hard 未完成

310 最小高度树 medium 未完成

动态规划

dp三要素，定义状态，初始状态，状态转移

70 爬楼梯 easy

题目说可以跨一步或者两步，动态规划最重要就是有一个状态转移方程，f(x)=f(x−1)+f(x−2)，你可以理解为，我走到x级的时候，我的方案数量就是走到x-1级的所有数量加上我走到x-2级的所有数量。怎么理解呢？比如我知道x-1级的所有方案数量，我再走一步就可以到达x级，同理，x-2级也是这样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int climbStairs(int n) {
        if (n <= 2) {    //注意力扣是计算1到45级阶梯,0是不算的，然后的话我们的状态转移方程是需要前一级和前前一级的，所以1和2是要已知的。
            return n;
        }
        int pre2 = 1, pre1 = 2, cur = 0; //pre2代表前两级，这里初始的1代表只有一个方案，也就是上第一级楼梯只有一个方案，pre1代表前一级楼梯，可以理解为上第二级楼梯的方案有两种，要么跨两步，要么就是连续走一步。
        for (int i = 2; i < n ; i++) {  //注意别忘了从第三级楼梯开始，这里和n（就是直接为多少级）含义不一样，不要混淆，因为这个for循环是计数用的，i=2代表从第三级开始。
            cur = pre1 + pre2; 
            pre2 = pre1;
            pre1 = cur;
        }
        return cur;
    }
}

198 打家劫舍 medium

直接说大于两间房的情况，那么有两种情况1.偷窃第k间房屋，那么就不能偷窃第k-1间房屋，偷窃总金额为前k-2间房屋的最高总金额与第k间房屋的金额之和。2.不偷窃第k间房屋，偷窃总金额为前k−1间房屋的最高总金额。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int rob(int[] nums) {
        if(nums == null || nums.length == 0) {
            return 0;
        }
        int len = nums.length;
        if(len == 1) {
            return nums[0];
        }
        int first = nums[0], second = Math.max(nums[0],nums[1]);
        for(int i = 2; i < len; i++) {//从第三间房开始,每间房之和该房屋的前两间房的最高总金额有关，因此用一个滚动数组，每个时刻只存储前两间房的最高金额。
            int temp = second;//一个temp来保存先
            second = Math.max(first + nums[i], second);//这时候开始找最大值
            first = temp;
        }
        return second;
    }
}

413 等差数列划分 medium

首先要注意至少是三个元素才可以，其次注意子数组也算，比如[1,2,3,4]这个就可以有[1, 2, 3]、[2, 3, 4] 和 [1,2,3,4] 三个等差数组。下面t++是不太好理解的，可以看官方解释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int numberOfArithmeticSlices(int[] nums) {
        int len = nums.length;
        if(len == 1 || len == 2) {
            return 0;
        }
        int d = nums[1] - nums[0], t = 0, ans = 0;
        for(int i = 2; i < len; i++) {
            if(nums[i] - nums[i - 1] == d) {
                ++t;
            } else {
                d = nums[i] - nums[i - 1];//否则重新计算d，比如可以试试[1,2,3,8,9,10]，答案是2个
                t = 0;
            }
            ans += t;
        }
        return ans;
    }
}

64 最小路径和 medium

首先要注意，路径只能向下或者向右，其次，返回的是最后路径的大小，而不是路径本身。本方法是创建一个最小路径的矩阵，也就是每个位置记录从左上角到这里最小值，最后返回右下角位置的值即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int minPathSum(int[][] grid) {
        if (grid == null || grid.length == 0 || grid[0].length == 0) {//这道题是二维矩阵的题
            return 0;
        }
        int rows = grid.length, columns = grid[0].length;
        int[][] dp = new int[rows][columns];
        dp[0][0] = grid[0][0];
        for (int i = 1; i < rows; i++) {     //考虑第一行的情况，只能往右边走，所以新构建的dp矩阵是dp左边元素加grip[i][0]的距离，再次说明dp矩阵表示距离
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        for (int j = 1; j < columns; j++) {   //考虑第一列的情况
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }
        for (int i = 1; i < rows; i++) {    //考虑里面的元素，请注意，务必先考虑完第一行和第一列的元素才能写这里，否则我们不知道怎么找上一个元素的距离，因为里面的元素也是和左边和上面元素相关
            for (int j = 1; j < columns; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[rows - 1][columns - 1];//构建完后返回最后一个元素的值即可
    }
}

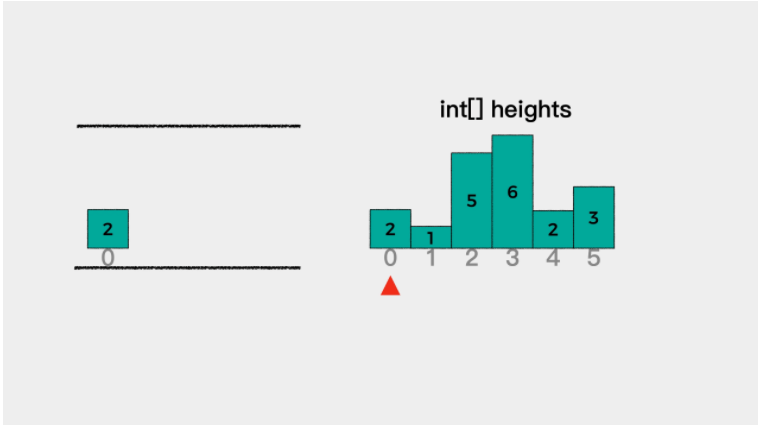
542 01矩阵 medium

和上一题一样，构建一个距离矩阵，但是本题又和上一题不太一样哦，是寻找每个元素距离0最近的距离。只有 水平向左移动 和 竖直向上移动，只有 水平向右移动 和 竖直向下移动。本题的思路是这个点周围的邻居到0的最小距离+1就是这个点到0的最短距离。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    public int[][] updateMatrix(int[][] mat) {
        int m = mat.length, n = mat[0].length; 
        int[][] dist = new int[m][n];
        for (int i = 0; i < m; i++) {  //初始化二维数组全部最最大值
            Arrays.fill(dist[i], Integer.MAX_VALUE / 2);//填充一维数组只需要Arrays.fill(Object[] ary, Object val)赋值，那么二维数组就需要一个循环。
        }
        for (int i = 0;i < m; i++) {  //初始化位置为0的元素距离就是0
            for (int j = 0; j < n; j++) {
                if (mat[i][j] == 0) {
                    dist[i][j] = 0;
                }
            }
        }
        //动态规划务必注意要找前一个的状态。至于为什么本题只需要左上和右下，可以看题解的评论，当然了，你也可以选择右上(右上角到左下角遍历)和左下(左下角到右上角遍历)。

        //只有 水平向左移动 和 竖直向上移动，注意动态规划的计算顺序
        //从左上角到右下角遍历,为什么左上是从左上角开始遍历，因为这是DP，需要知道前一步的状态。
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i - 1 >= 0) {//检查上邻居,if条件是为了有上邻居，而不至于越界。
                    dist[i][j] = Math.min(dist[i][j], dist[i - 1][j] + 1); 
                }
                if (j - 1 >= 0) {//检查左邻居,if条件是为了有左邻居，而不至于越界。
                    dist[i][j] = Math.min(dist[i][j], dist[i][j - 1] + 1); 
                }                
            }
        }
        //只有 水平向右移动 和 竖直向下移动，注意动态规划的计算顺序
        //从右下角到左上角遍历
        for (int i = m - 1; i >= 0; i--) {
            for (int j = n - 1; j >= 0; j--) {
                if (i + 1 < m) {//检查下邻居
                    dist[i][j] = Math.min(dist[i][j], dist[i + 1][j] + 1); 
                }
                if (j + 1 < n) {//检查右邻居
                    dist[i][j] = Math.min(dist[i][j], dist[i][j + 1] + 1); 
                }                
            }
        }
        return dist;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
为啥只用左上和右下就行？ 用最简单的只有一个0的来示例（来自网友的图）

1111
1111
1011
1111

左上（左邻居和上邻居）之后变成(其中-表示int最大值)
----
----
-012
-123

接下来的右下就是取某个点的右上和左下其中比较小的值 加一 就行 现在根据已知的右下角这一坨 已经可以推出其余的全部了 比如左下角那一坨

----
----
1012
2123

右上角那一坨

-234
-123
1012
2123

还有最终左上角的那一坨

3234
2123
1012
2123

我自己的一个小例子
10
01

左上后
m0
m1

右下后
10
21

221 最大正方形 medium

首先需要注意,dp[i][j]是以i，j坐标为右下角的正方形边长。

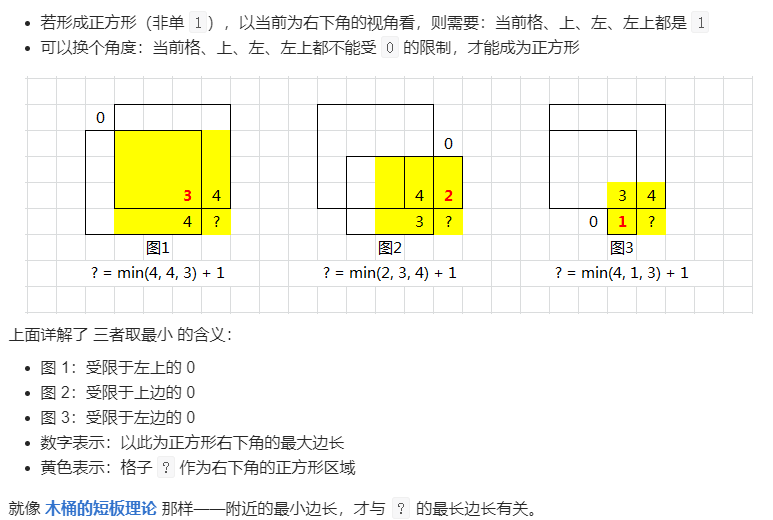
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int maximalSquare(char[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        int maxsize = 0;
        int m = matrix.length, n = matrix[0].length;
        int [][] dp = new int[m][n];
        for (int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if (matrix[i][j] == '1') { 
                    if (i == 0 || j == 0) {//在边界的情况
                        dp[i][j] = 1;
                    }
                    else {//不在边界，等于这个坐标的左边，上边，左斜上边的最小值加上1，同时也是本题的动态规划转移方程。
                        dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i][j - 1]) +1;
                    }
                } 
                maxsize = Math.max(maxsize, dp[i][j]);
            }
        }
        return maxsize * maxsize;
    }
}

下面一个图来自网友，解释了为什么用左边，上边，左斜上边的最小值。

279 完全平方数 medium

推荐看这个作者的讲解，非常好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 0;//初始化0的位置
        for (int i = 1; i < n + 1; i++) {
            dp[i] = i;//每个位置最差的情况就是i个数，比如dp[12]最大就是12个1来组成
            for (int j = 1; i - j * j >=0 ; j++) {//你不能f[12]来一个16的平方数，所以i-j*j要大于等于0
                dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
            }
        }
        return dp[n];
    }
}
/*
这里解释下状态转移方程
比如递推到找f[11]
那么可以拆成f[2] + 1（这个1表示9这个完全平方数，也可以理解为f[11 - 9]再加上一个9就能组成f[11]的数量，这里不要混了，f[n]表示的是一个数量，加9这个平方数就是加一个1，这也是为什么状态转移方程是+1）
还能拆成f[7] + 4这个平方数, f[7]也就是f[11 - 4]，所以f[7]的数量，再加一个1，可以表示成f[11]的数量。
还能拆成f[10] + 1这个平方数，同理不再叙述
然后找他们最小值即可。
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
//根据书上例子写的，上面那个更好理解
class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        for (int i = 1; i <= n ; i++) {
            for (int j = 1;  j * j <= i ; j++) {
                dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
            }
        }
        return dp[n];
    }
}

91 解码方法 medium

这个题思考了比较久，题解是根据书上改成java的，虽然比较长，但是好理解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int numDecodings(String s) {
        int n = s.length();
        if (n == 0) return 0;
        int prev = s.charAt(0) -48;//因为s是字符串，我们提取出来的数字是ASCII码，48是0的ASCII码，这样写转成数字，比如'1'就转成1

        if (prev == 0) return 0;
        if (n == 1) return 1;
        int[] dp = new int[n + 1];
        Arrays.fill(dp,1);//全部位置首先置为1，如果单独dp[0]为1，会发现s=12有错误，我一开始以为只置第0个数就行。
        for (int i = 2; i <= n; i++) {
            int cur = s.charAt(i - 1) - 48;
            if ((prev == 0 || prev > 2) && cur == 0) {//如果当前为0，并且前一个数是0或者大于2，无法解码,注意if中第一个括号很关键，比如是组合在一起(prev == 0 || prev > 2)
                return 0;
            }
            if (prev == 1 || prev == 2 && cur < 7) {//如果前一个数是1或者2，并且当前数小于7，考虑组合问题
                if (cur!=0) {//首先当前数不为0，也就是当前数和之前那个数可以组合在一起
                    dp[i] = dp[i - 2] + dp[i - 1];//
                } else {//当前数虽然等于0，但是前一个数为1或者2，也可以组合成10,20，也就是我们当前数是不能单独解码
                    dp[i] = dp[i - 2];
                }
            } else {//无法进行组合了，只能单独解第二个数
                dp[i] = dp[i - 1];
            }
            prev = cur;
        }
        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
理解过程
这个题是返回解码方法的总数，
首先定义一个长为n+1的数组，dp[2]就表示前2个数的解码方法总数，所以最后返回dp[n]就代表题目要求的答案了。

如果第一个数字就是0，那不用问，永远解不出来，规则上01和1是不一样的，没有01这个解码。
其次声明好dp数组，长度为n+1，并且全部位置初始化为1，后面会讲到为什么f[0]也要设置为1。
我们要清楚，声明了prev和cur，就是为了看看当前数和前一个数能不能组合起来解码.
进入判断循环,i从2开始，这是为了配合dp数组，因为我们说了dp[i]表示前i个数的解：
       那么cur就是s[i - 1]了，这是s数组的第二个数，prev我们在前面已经声明了。
       首先就是判断无法解码的情况，也就是cur为0，prev也为0或者prev大于2，既不能自己单独解码，也不能和前面组合解码。
       然后判断可以解码的情况，有组合解码和单独解码
          组合解码又分为11~19,21~26，因为10和20比较特殊，前者既能单独解码，又能组合解码，后者只能单独解码的两位数
          然后单独解码就是只能单独一个解码
       下一轮判断，把cur变成prev



为什么f[0]也为1？ 这里摘抄了网友的一个不错的理解：
f[0]代表前0个数字的方案数，这样的状态定义其实是没有实际意义的，但是f[0]的值需要保证边界是对的，即f[1]和f[2]是对的。
比如说，第一个数不为0，那么解码前1个数只有一种方法，将其单独解码，即f[1] = f[1 - 1] = 1。
解码前两个数，如果第1个数和第2个数可以组合起来解码，那么f[2] = f[1] + f[0] = 2 ，否则只能单独解码第2个数，即f[2] = f[1] = 1。
因此，在任何情况下f[0]取1都可以保证f[1]和f[2]是正确的，所以f[0]应该取1。

然后的话，我们在代码中有一个10和20的特殊解码，dp[i] = dp[i - 2]。因为这里说了如果只能单独解码的话，就f[1] = f[1 - 1] = 1。

实在不能理解。试试s=20,s=23，尝试自己去理解一下。

139 单词拆分 medium

这道题类似于完全平方数分割。然后看到评论题解说用背包问题：单词就是物品，字符串s就是背包，完全背包问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        int n = s.length();
        boolean[] dp = new boolean[n + 1];
        dp[0] = true;
        for(int i = 1; i <= n; i++) {
            for(int j = 0; j < i; j++) {
                if(wordDict.contains(s.substring(j,i)) && dp[j] == true) { //contains比较少用，mark
                    dp[i] = true;
                }
            }
        }
        return dp[n];
    }
}
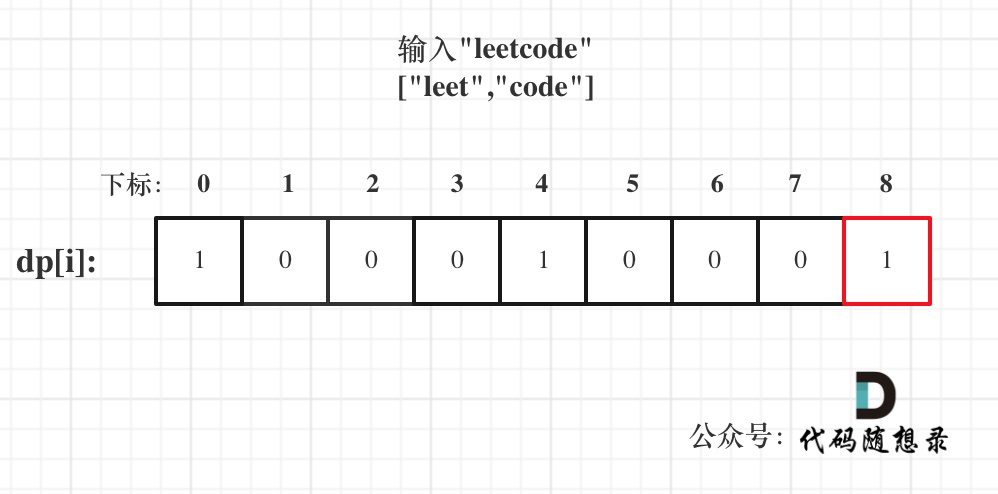
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
卡哥将得很详细，复制一下记录
单词就是物品，字符串s就是背包，单词能否组成字符串s，就是问物品能不能把背包装满。

拆分时可以重复使用字典中的单词，说明就是一个完全背包！

动规五部曲分析如下：

1.确定dp数组以及下标的含义
dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词。

2.确定递推公式
如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true。（j < i ）。

所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。

3.dp数组如何初始化
从递归公式中可以看出，dp[i] 的状态依靠 dp[j]是否为true，那么dp[0]就是递归的根基，dp[0]一定要为true，否则递归下去后面都都是false了。

那么dp[0]有没有意义呢？

dp[0]表示如果字符串为空的话，说明出现在字典里。

但题目中说了“给定一个非空字符串 s” 所以测试数据中不会出现i为0的情况，那么dp[0]初始为true完全就是为了推导公式。

下标非0的dp[i]初始化为false，只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词。

4.确定遍历顺序
题目中说是拆分为一个或多个在字典中出现的单词，所以这是完全背包。

还要讨论两层for循环的前后循序。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

本题最终要求的是是否都出现过，所以对出现单词集合里的元素是组合还是排列，并不在意！

那么本题使用求排列的方式，还是求组合的方式都可以。

即：外层for循环遍历物品，内层for遍历背包 或者 外层for遍历背包，内层for循环遍历物品 都是可以的。

但本题还有特殊性，因为是要求子串，最好是遍历背包放在外循环，将遍历物品放在内循环。

如果要是外层for循环遍历物品，内层for遍历背包，就需要把所有的子串都预先放在一个容器里。（如果不理解的话，可以自己尝试这么写一写就理解了）

所以最终我选择的遍历顺序为：遍历背包放在外循环，将遍历物品放在内循环。内循环从前到后。

5.举例推导dp[i]
以输入: s = "leetcode", wordDict = ["leet", "code"]为例，dp状态如图：
（在下方）
dp[s.size()]就是最终结果。


ps:
五部曲中第一部是最困难的. 一般都是遵循"题目问什么, 就把`dp[]设置成什么


作者：carlsun-2
链接：https://leetcode.cn/problems/word-break/solution/dai-ma-sui-xiang-lu-139-dan-ci-chai-fen-50a1a/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

300 最长递增子序列 medium

首先说明题目说的升序是严格升序，比如777长递增子序列就只有7，也就是长度只有1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//跟之前的题目有点不同的是dp声明不需要额外声明多一个，因为本题是返回最大值。同样也是卡尔的题解。
class Solution {
    public int lengthOfLIS(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n];
        Arrays.fill(dp,1);//别忘了初试填充1
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {//这里还有一个循环
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);//状态转移方程很重要，注意这里是max，而不是比较dp[i], dp[j] + 1
                }               
            }
        }
        int res = 0;
        for (int i = 0; i < n; i++) {//找出最大值即可
            res = Math.max(res,dp[i]);
        }
        return res;
    }
}
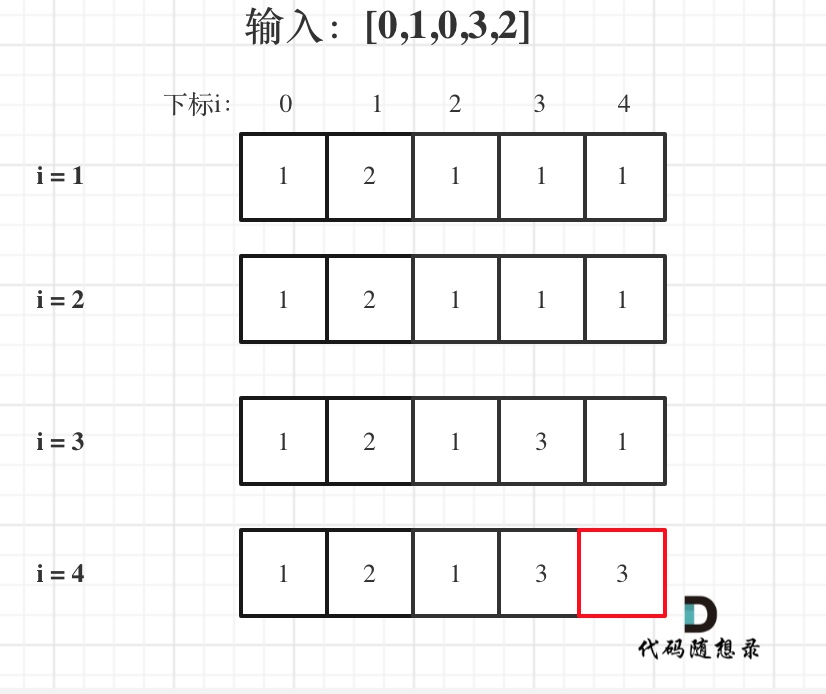
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
卡哥动态规划五部曲
最长上升子序列是动规的经典题目，这里dp[i]是可以根据dp[j] （j < i）推导出来的，那么依然用动规五部曲来分析详细一波：

1.dp[i]的定义
dp[i]表示i之前包括i的以nums[i]结尾最长上升子序列的长度

2.状态转移方程
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。

所以：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

注意这里不是要dp[i] 与 dp[j] + 1进行比较，而是我们要取dp[j] + 1的最大值。

3.dp[i]的初始化
每一个i，对应的dp[i]（即最长上升子序列）起始大小至少都是1.

4.确定遍历顺序
dp[i] 是有0到i-1各个位置的最长升序子序列 推导而来，那么遍历i一定是从前向后遍历。

5.举例推导dp数组
输入：[0,1,0,3,2]，dp数组的变化如下：

1143 最长公共子序列 medium

需要注意的是本题要求：”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。本题单纯是动态规划，不是背包问题哦。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//一般如果返回dp数组，就好像申请的长度加+1，这样是为了好处理，
class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int n = text1.length(), m = text2.length();
        int[][] dp = new int[n + 1][m + 1];//除了定义dp，它还会全部设置为0，像之前有些题是初始化为1，要注意对比
        for (int i = 1; i <= n; i++) {//从1开始
            for (int j = 1; j <= m; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {//上面是从1开始，所以我们对比的第一个数是i-1和j-1
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
                }
            }
        }
        return dp[n][m];
    }
}
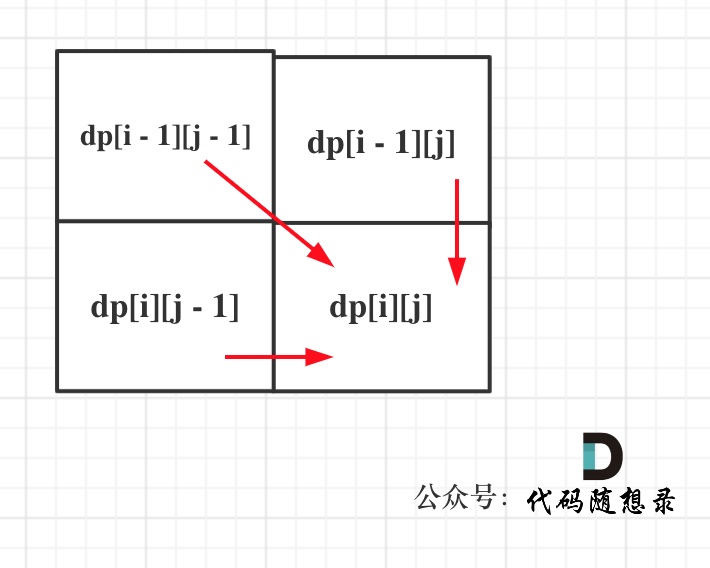
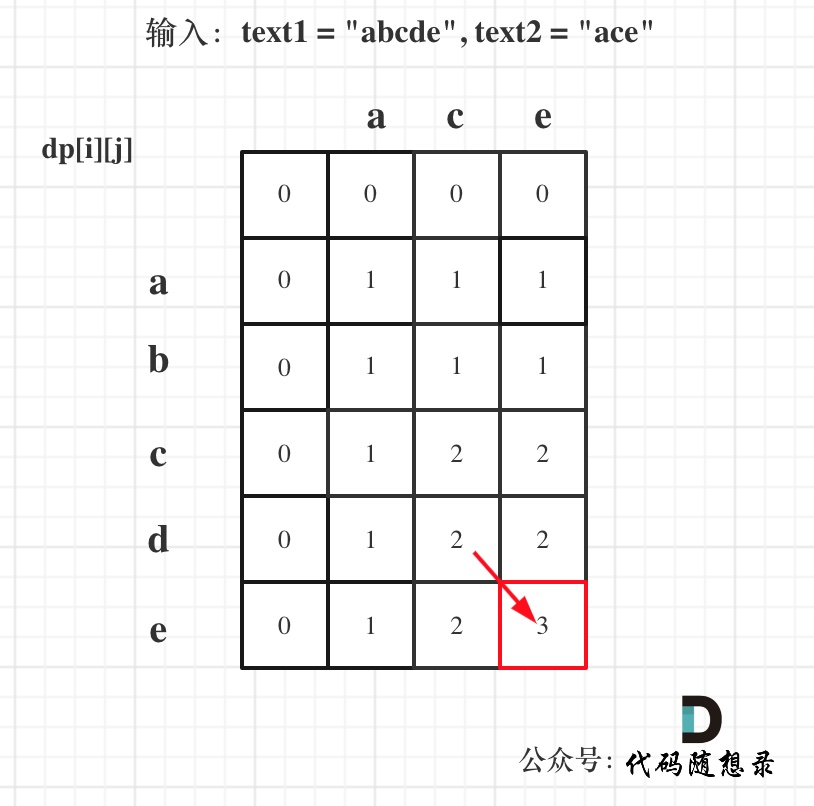
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
卡哥的解释比较好懂
1.确定dp数组（dp table）以及下标的含义
dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]

有同学会问：为什么要定义长度为[0, i - 1]的字符串text1，定义为长度为[0, i]的字符串text1不香么？

这样定义是为了后面代码实现方便，如果非要定义为为长度为[0, i]的字符串text1也可以，大家可以试一试！

2.确定递推公式
主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

3.dp数组如何初始化
先看看dp[i][0]应该是多少呢？

test1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;

同理dp[0][j]也是0。

其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为0。

4.从递推公式，可以看出，有三个方向可以推出dp[i][j]，如图：
(下面第一张图)

5.举例推导dp数组
以输入：text1 = "abcde", text2 = "ace" 为例，dp状态如图：
(下面第二张图)


416 分割等和子集 medium（0-1背包）

本题是0-1背包问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public boolean canPartition(int[] nums) {
        if (nums == null || nums.length == 0) {
            return false;
        }
        int sum = 0;
        for (int num:nums){
            sum += num;
        }
        if (sum % 2 != 0) return false;
        int target = sum / 2;
        int[] dp = new int[target + 1];//已经默认初始化为0
        for (int i = 0; i <nums.length; i++) {
            for (int j = target; j >= nums[i]; j--) {//逆向循环，而且注意j >= nums[i]，我自己的理解是当可以放进去时候的操作，注意物品i的重量是nums[i]，其价值也是nums[i]
                dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            }
        }
        return target == dp[target];
    }
}

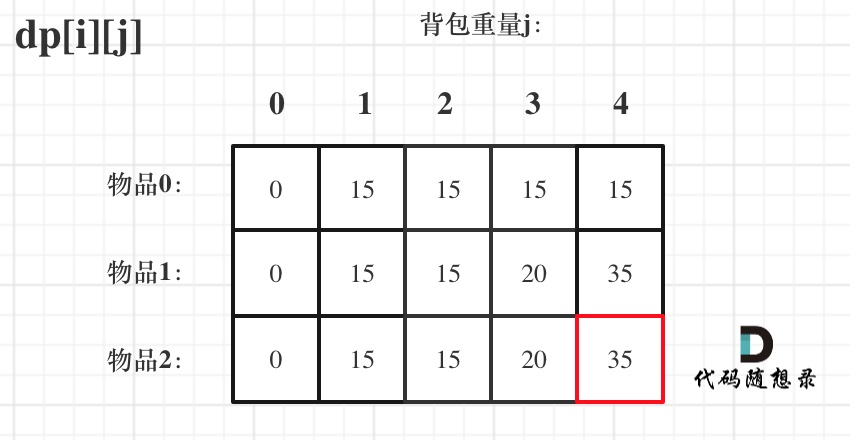
具体看Carl的解释，写得挺好，需要好好理解转移方程Math.max(dp[j], dp[j - nums[i]] + nums[i]);

1
2
3
4
5
6
7
8
9
10
0-1背包问题和完全背包问题的区别的是，一个是物品只能拿一次，一个物品无限拿。
循环上也有区别：
0-1背包问题物品的迭代放外层，里层的体积或价值逆向遍历，物品放外面，循环完就没了，也就是物品只能拿一次。
完全背包对物品的迭代放里层，外层的体积或价值正向遍历，物品放里面，每次外层循环都会重新循环物品，也就是物品是无限拿的。
本题可以对比看看139。
简单说明几点
dp[j] 表示： 容量为j的背包，所背的物品价值可以最大为dp[j]，我们本题的容量是sum/2 + 1来确定的，本题上的dp[j]表示背包总容量是j，最大可以凑成j的子集总和为dp[j]

本题，相当于背包里放入数值，那么物品i的重量是nums[i]，其价值也是nums[i]。
所以递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);

背包问题全理解

下面是背包问题总结（Carl的笔记加上我自己的理解）：

二维dp数组01背包
1.确定dp数组以及下标的含义
对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。要时刻记着这个dp数组的含义，也就是一共涉及三个数，一个是物品，一个是容量，然后数组里面存的是价值，数组如图展示：

2.确定递推公式
再回顾一下dp[i][j]的含义：从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

那么可以有两个方向推出来dp[i][j]，

不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。)
放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值
所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

这里一开始不能理解dp[i - 1][j - weight[i]] + value[i]，因为我一开始想，万一背包里面本来就有东西，为什么仅仅判断j>weight[i]就说能放进去呢?是我多虑了，因为二维数组覆盖了所有情况呀。
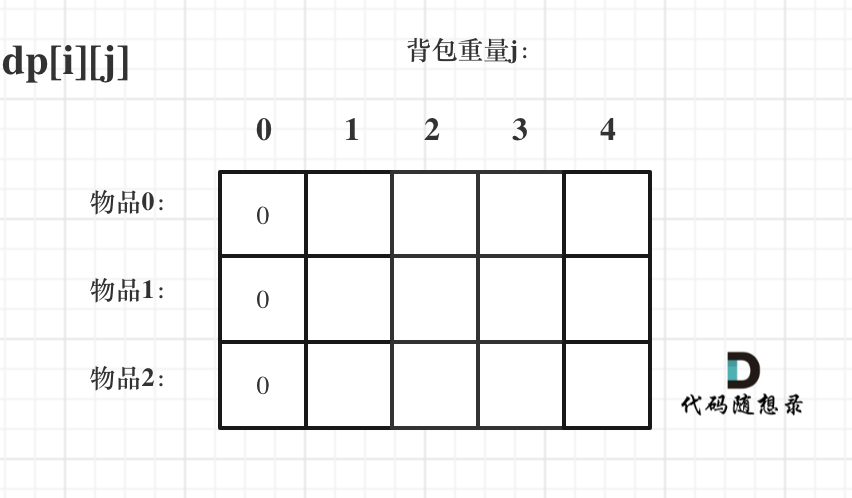
举个例子，背包容量是4，刚好我们物品大小也是4，这时候j-4＝0，我们会去检查i-1情况下0的价值，如果背包容量是5，那就去检查j-4=1时候的价值，所以不存在说本来有东西，他会跳到上一步检查的。

3.dp数组如何初始化
关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。如图：

再看其他情况。

状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。

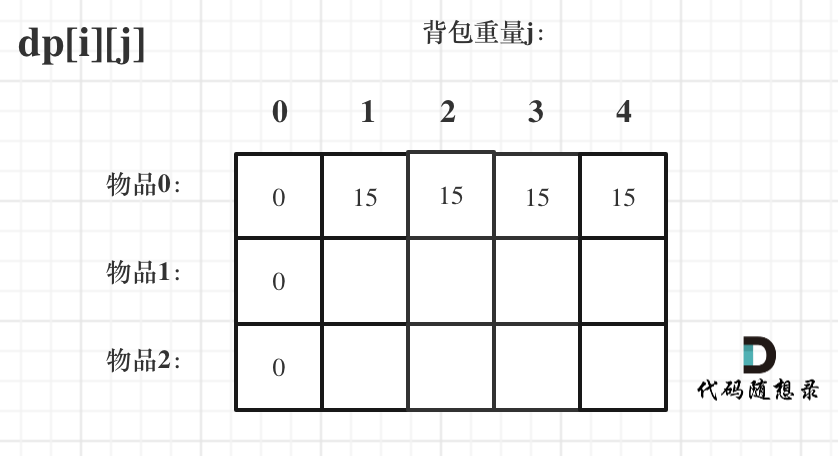
dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。

那么很明显当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。

当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。
此时dp数组初始化情况如图所示

dp[0][j] 和 dp[i][0] 都已经初始化了，那么其他下标应该初始化多少呢？

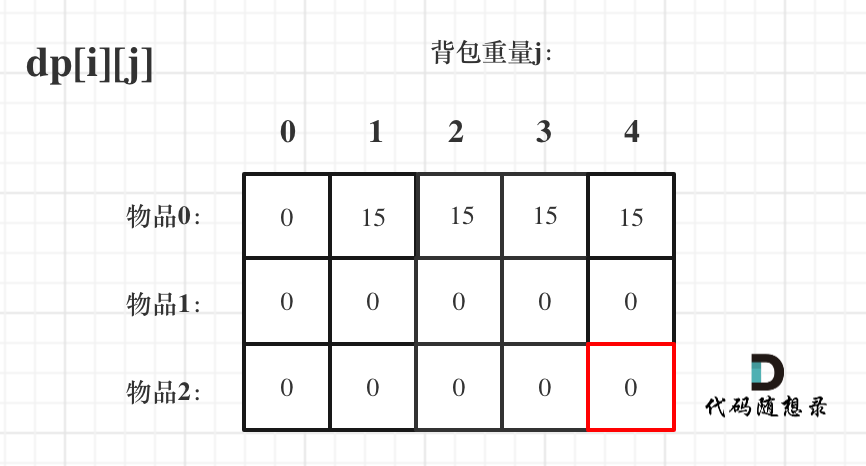
其实从递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由左上方数值推导出来了，那么 其他下标初始为什么数值都可以，因为都会被覆盖。

初始-1，初始-2，初始100，都可以！

但只不过一开始就统一把dp数组统一初始为0，更方便一些。

4.确定遍历顺序
在如下图中，可以看出，有两个遍历的维度：物品与背包重量

那么问题来了，先遍历 物品还是先遍历背包重量呢？

其实都可以！！ 不过这里针对的是二维数组。

5.举例推导dp数组
来看一下对应的dp数组的数值，如图

一维dp数组01背包
1.确定dp数组的定义
在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。

2.一维dp数组的递推公式
dp[j]为 容量为j的背包所背的最大价值，那么如何推导dp[j]呢？

dp[j]可以通过dp[j - weight[i]]推导出来，dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。

dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。（也就是容量为j的背包，放入物品i了之后的价值即：dp[j]）

此时dp[j]有两个选择，一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j]，即不放物品i，一个是取dp[j - weight[i]] + value[i]，即放物品i，指定是取最大的，毕竟是求最大价值，

所以递归公式为：

1
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

3.一维dp数组如何初始化
关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。

那么dp数组除了下标0的位置，初始为0，其他下标应该初始化多少呢？

看一下递归公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。

这样才能让dp数组在递归公式的过程中取的最大的价值，而不是被初始值覆盖了。

那么我假设物品价值都是大于0的，所以dp数组初始化的时候，都初始为0就可以了。

4.一维dp数组遍历顺序

1
2
3
4
5
6
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

这里大家发现和二维dp的写法中，遍历背包的顺序是不一样的！

二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。

为什么呢？

倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！

看完之后发现，也就是二维数组必须要顺着，如果用一维数组处理，要倒着，至于为什么这里需要好好看卡哥的网站。

474 一和零 medium （0-1背包）

注意这个不是多重背包问题。本题就是0-1背包问题。具体看卡哥解释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/*
这个题相当于有两个维度的背包，m和n。
而不同长度的字符串就是不同大小的待装物品。
这里是求子集的个数。
*/
class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int[][] dp = new int[m + 1][n + 1];//虽然这个是二维数组，但是不是我们理解那个用二维数组解决的背包问题，这是拥有两个维度的背包，实际上我们是用滚动数组来做的。
        for (String str:strs) {//先遍历物品
            int onenum = 0, zeronum = 0;//每次遍历物品都要重新计算
            for (char c : str.toCharArray()) {//这个写法mark
                if (c == '0') {//统计每个物品的0和1的数量，注意我们是一个字符串当成一个物品。
                    zeronum++;
                } else {
                    onenum++;
                }
            }
            //字符串的zeroNum和oneNum相当于物品的重量（weight[i]），字符串本身的个数相当于物品的价值value[i]
            for (int i = m; i >= zeronum; i--) {//请注意这里是在遍历物品的内部循环，然后这个m是背包容量，逆序遍历
                for (int  j = n; j >= onenum; j--) {//背包的第二个维度，也是逆序遍历
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeronum][j - onenum] + 1);
                }
            }            
        }
        return dp[m][n];
    }
}

322 零钱兑换 medium（完全背包）

每种币的数量是无限，本题属于完全背包问题。注意这个题要取最小的。讲解链接。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//这个更好理解，先遍历背包，再遍历物品，和之前不太一样的是，我们取最小的，这点对初始化很重要哦，而且在判断上也要注意一点。
public class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);//除了0位置，必须要初始化为最大值，不然你要是都是0，用min的时候就都变成0了，被覆盖掉了
        dp[0] = 0;//同上面一样的初始化
        for (int i = 1; i <= amount; i++) {//先遍历背包
            for (int j = 0; j < coins.length; j++) {//遍历物品，这种写法就比较好理解用无限硬币
                if (i- coins[j] >= 0 && dp[i - coins[j]] != Integer.MAX_VALUE) {//后面这个不为max值很重要，不然到最后max值会变成负数，然后有这个判断就可以跳过。只有dp[i-coins[j]]不是初始最大值时，该位才有选择的必要
                    dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);//必须要背包容量打于当前的coin大小才进入这一步
                }
            }
        }
        if (dp[amount] == Integer.MAX_VALUE) return -1;
        return dp[amount];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//物品是coin，背包是amount，这个写法是先遍历物品，再遍历背包，我感觉不如上面一个好理解。
class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);//因为求min，所以要把除了0位置的地方赋值为最大值
        dp[0] = 0;//把0位置赋值为0，因为你的钱要是为0，就不可能用任何硬币来组合。
        for(int i = 0; i < coins.length; i++) {//物品外循环
            for (int j = coins[i]; j <= amount; j++) {//背包内循环 当然这个题也可以反过来循环，不过if条件要改变。本题钱币数量可以无限使用，那么是完全背包。所以遍历的内循环是正序
                if ((dp[j - coins[i]]) != Integer.MAX_VALUE) {//只有dp[j-coins[i]]不是初始最大值时，该位才有选择的必要
                    dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
                }
            }
        }
        if (dp[amount] == Integer.MAX_VALUE) return -1;
        return dp[amount];
    }
}
/*这里一开始写内循环是j = 0，但是我们要每个时候都要想dp[j]代表什么含义，当j为0，直接减去coin就是负数了，不过还是没特别理解，多做题把。
dp[j]：凑足总额为j所需钱币的最少个数为dp[j]*/

72 编辑距离 hard

注意word1变成word2，中间的操作不需要指定多少次，反正直到变成word2，增删替都能无数次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length(), n  = word2.length();
        int[][] dp =  new int[m + 1][n + 1];
        for (int i = 0;i <=m; i++) {
            dp[i][0] = i;
        }
        for (int j = 0; j <=n; j++) {
            dp[0][j] = j;
        }

        for (int i = 1; i <=m ;i++) {
            for (int j = 1; j <=n; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                }           
            }
        }
        return dp[m][n];
    }
}
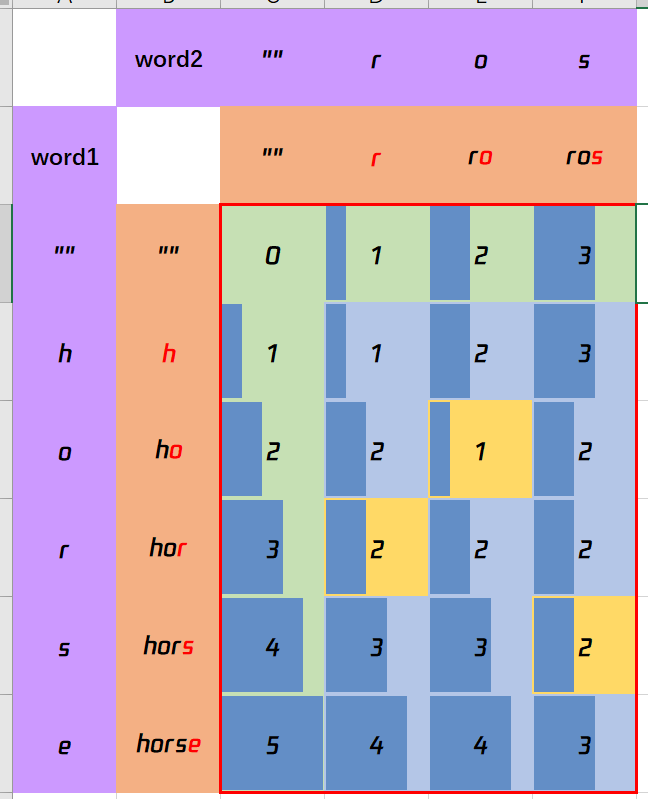
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
这个需要理解几个点，跟其他动态规划有点不一样，但是又是相似的套路。
1.dp[i][j]含义：dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。
注意是到这个位置结尾的单词，而不是整个单词。
时刻理解dp含义！时刻理解dp含义！时刻理解dp含义！时刻理解dp含义！
2.注意删除操作和增加操作是一回事

理解 word1 上的删除等价 word2 上的增加, word1 上的增加等价于 word2 上的删除，另外一个博主的理解：dp[i-1][j-1] 表示替换操作，dp[i-1][j] 表示删除操作，dp[i][j-1] 表示插入操作。

按照我自己理解把
删除操作：我们这时候要删掉word这个位置的元素，那么我向word1前推一个字符查看那时候的步数，也就是dp[i-1]，j位置不变，然后再加上删除这个操作就可以+1步数。
替换操作：word1和word2这个位置没有删除，没有添加，那就同时推前面一个元素。
增加操作(等价于word2删除)：word1这个位置要增加元素操作，然后我们知道word1的增加等价于word2删除，那就dp[j-1]推前一个位置，i不变。
3.初始化和其他方法很不同，因为我们要理解dp[i][0]的含义，dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。

那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i，相反dp[0][j]就是对元素进行添加。

注意上面是i，而不是word1的长度，而不是word1的长度，而不是word1的长度，而不是word1的长度，务必时刻理解dp[i][j]的含义。

借一张图理解，比如ho和ro那个黄色格子(2,2)的意思就是(1,1)一样的步数，那么(1,1)的理解就是h变成r的过程步数，怎么变不重要，我们只关心步数。

650 只有两个键的键盘 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//复制算一次，粘贴算一次
class Solution {
    public int minSteps(int n) {
        int[] dp = new int[n + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);//求min务必要初始化最大值
        dp[1] = 0;//但是1是0，因为笔记本上本来就存在一个A，不需要操作

        for(int i = 2; i <= n; i++) {
            for (int j = 1; j <= i / 2; j++) {//也可写成 j <= i，不过除以2更好，要明白复制粘贴的意义，也就是翻倍的意思
                if (i % j == 0) {//必须要被除尽才可以，这样说明j个A可以通过复制粘贴得到i个A
                    dp[i] = Math.min(dp[i], dp[j] + i / j);//比如6可以除以3，也可以除以2，但是我们要拿最小次数来复制粘贴，当然这里只是打个比方，可能3和2次数一样
                }
            }
        }
        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
注意复制是一次操作，粘贴又是一次操作
总体思路：对每一个格子i（i个A），如果i可以被j除尽，说明j个A可以通过复制粘贴得到i个A，复制粘贴次数为i / j。
每个格子的意义：得到目前数量个A需要的最少操作次数
递推公式：dp[i] = min(dp[i], dp[j] + i / j)dp[i]=min(dp[i],dp[j]+i/j)，其中i % j == 0i
初始化：1个A不需要操作，初始化为0

作者：Reconcile
链接：https://leetcode.cn/problems/2-keys-keyboard/solution/dong-tai-gui-hua-jie-fa-by-reconcile-t3fr/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。


这里举个例子，dp[1]~dp[5]的情况是0 2 3 4 5 
到了dp[6]，答案也是5，因为6可以复制3的情况，然后再粘贴，那么3本身需要3次，6/3=2,3+2＝5。也就是i/j是复制粘贴的次数。

这里理解下为什么是i/j次，比如dp[8]，
如果我们是复制dp[2]的情况，需要8/2=4次，首先复制AA，然后粘贴三次，一共四次操作加上dp[2]操作。
如果复制dp[4]的情况，8/4=2，首先复制AAAA，然后粘贴一次，一共2次操作加上dp[4]操作。
如果复制dp[1]的情况，8/1=8，首先复制A，然后粘贴七次，一共8次操作加上dp[1]操作。
当然，上面的情况要比较然后取最小值。

10 正则表达式匹配 hard(未完成)

121 买卖股票的最佳时机 easy

这个题目的股票只买卖一次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//动态回归，符合本章节，但是最简单还是贪心算法，因为这个题目的股票只买卖一次。这个做法没有具体去理解，可以看卡哥解释。
class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length == 0) return 0;
        int length = prices.length;
        // dp[i][0]代表第i天持有股票的最大收益
        // dp[i][1]代表第i天不持有股票的最大收益
        int[][] dp = new int[length][2];
        int result = 0;
        dp[0][0] = -prices[0];//一开始现金是0，那么加入第i天买入股票现金就是 -prices[i]， 这是一个负数
        dp[0][1] = 0;//第0天不持有股票最大收益
        for (int i = 1; i < length; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
            dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);
        }
        return dp[length - 1][1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
//贪心算法，最简单这个
//取左边低值，取右边高值即可，因为只买卖一次。
class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int low = Integer.MAX_VALUE;
        int result = 0;
        for (int i = 0; i < n; i++) {
            low = Math.min(low, prices[i]);
            result = Math.max(result, prices[i] - low);
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//这个答案是超时的，但至少是自己想出来的，哎，太暴力了。
class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[] dp = new int[n];
        int result = 0;
        for (int i = 0; i < n - 1; i++) {
            for (int j = i + 1; j < n; j++) {
                if (prices[j] - prices[i] > 0) {
                    dp[i] = Math.max(dp[i], prices[j] - prices[i]);
                    result = Math.max(result, dp[i]);
                }
            }
        }
        return result;
    }
}

188 买卖股票的最佳时机 IV

这个题目是可以最多交易K次，也就是你交易的次数可以少于k，但是必须在再次购买前出售掉之前的股票，而且利润要最大化。k为1，也就是可以买一次，卖一次，这个算交易一次。k为2，也就是一共可以买2次，卖两次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int maxProfit(int k, int[] prices) {
        if (prices.length == 0) return 0;
        int n = prices.length;
        int[][] dp = new int[n][2 * k + 1];
        for (int i = 1; i < 2 * k; i += 2) {//只初始化第0天的买入状态，然后其他是默认0
            dp[0][i] = -prices[0];
        }

        for (int i = 1; i < n; i++) {//第0天上面已经初始化好了，所以直接从第一天开始
            for (int j = 0; j < 2 * k - 1; j += 2) {//状态要从0开始，然后隔两个操作，长度是2k-1是因为我们总的长度是2k+1，然后现在隔2来操作，只有长度为2k-1才不至于越界，因为2k-1+2为2k+1，这是总长度
                dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]); //处理买入股票的状态
                dp[i][j + 2] = Math.max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);//处理卖出股票的状态
            }
        }
        return dp[n - 1][k * 2];//i的大小是n，那么最后的坐标就是n-1,j的大小是k*2+1，那么坐标就是k*2。

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
重点理解
dp长度是dp[price.length][2 * k + 1]
也就是每一天都有2k+1个状态


务必清楚dp[i][j]的意思是第i天买入股票的状态是j
最少有3个状态，0代表不操作，1代表第一次买入，2代表第第一次卖出，如果你的k是2，那么也许还有第二次买入，第二次卖出，当然了，你的交易次数最大是k，不一定非要用完k

首先是初始化，dp[0][i] = -prices[0];表示买入，因为你买入就是钱是负数，然后如果卖出的话，当前价格加上上次买入的状态，就是你的利润，如-1+5=4，一开始我们买入价格是1，置为负数，然后卖出的时候价格是4，就可以得到利润了，还需要注意我们必须买入第二次的时候，第一次已经交易完毕了，不能连续买入而没有卖出，所以，只要是买入状态，就是负数。

其次是状态的改变：
dp[i][1]状态有两个情况，我们上面说1就是买入状态，但是这里需要更详细说明，1可能是两个操作，买入和不操作状态。
不操作就是延续前一天的状态：dp[i - 1][1]：前一天买入的状态
买入就是dp[i - 1][0] - price[0]：前一天不操作的状态

dp[i][2]状态有两个情况，我们上面说2就是卖出状态，但是这里需要更详细说明，2可能是两个操作，卖出和不操作状态。
不操作就是延续前一天的状态：dp[i - 1][2]：前一天不操作的状态
卖出就是dp[i - 1][1] + price[i]：前一天买了股票的钱再加上今天卖出的价格

309 最佳买卖股票时机含冷冻期 medium

和上一题的区别是，多了一个冷冻期，也就是卖出的第二天不能买入股票，卡哥笔记。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        if (n == 0 || prices == null) return 0;
        int[][] dp = new int[n][4];
        dp[0][0] = -prices[0];
        for (int i = 1; i < n; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], Math.max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][3]);
            dp[i][2] = dp[i - 1][0] + prices[i];
            dp[i][3] = dp[i - 1][2];
        }
        return Math.max(dp[n - 1][1], Math.max(dp[n - 1][2], dp[n - 1][3]));
    }
}
1
2
3
4
5
6
主要是理解四个状态的情况和初始化的情况，具体看卡哥的笔记，这里简单写4个状态的意思
0：买入股票状态（今天买入股票，或者是之前就买入了股票然后没有操作）
1：两天前就卖出了股票，度过了冷冻期，一直没操作，今天保持卖出股票状态
2：今天卖出了股票
3：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！
其中1和2都是属于卖出股票的状态，只是分成更细的。

213

53

343

583

646

376

494

714

分治法

241 为运算表达式设计优先级 medium

注意本题只有加减乘三个符号，没有除号，这个博主讲得是最详细容易理解的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
//博主的答案，额外有些不明白的地方多加了解释，分治的思想就是把原问题分成子问题，然后再合并起来。
class Solution {
    public List<Integer> diffWaysToCompute(String expression) {
        return divideAndConquer(expression.toCharArray());//将字符串转换为字符数组
    }

    public static List<Integer> divideAndConquer(char[] expression){
        List<Integer> res = new ArrayList<>();
        //处理一个数字的情况也就是分治划分到最底层的时候
        //isOneNum函数用来判断当前的表达式是否为一个单独的数字
        if (isOneNum(expression)){
            int num = 0;
            //将该数字从char数组转换为一个int型数值
             for (int i=0;i<expression.length;i++){
                 num = num*10 +expression[i]-'0';//比如98，一开始num为9，下一个循环就是9*10+'8'-'0'即为98，这里注意下字符要中ASILL码转换
             }
             res.add(num);
            return res;
        }

        for (int i=0;i<expression.length;i++){
            if (!Character.isDigit(expression[i])){//扫描到有运算符的情况
                char[] left = new char[i];//生成左边表达式
                char[] right = new char[expression.length-i-1];//生成右边表达式
                //切分左右分治所使用的表达式数组
                System.arraycopy(expression,0,left,0,i);//复制左边数组，注意是不含i这个位置的运算符的，具体看下面的例子你就知道，i代表长度
                System.arraycopy(expression,i+1,right,0,expression.length-i-1);//复制右边数组
                //对左边的表达式在进行一次同样的操作  这里是体现分治的思想吧？
                List<Integer> leftList = divideAndConquer(left);
                //对右边的表达式在进行一次同样的操作
                List<Integer> rightList = divideAndConquer(right);
                //计算左右两个表达式在当前用来切分的运算符进行运算后得到的所有可能的结果
                List<Integer> tempRes = calculate(leftList,rightList,expression[i]);
                //将这些结果加入最后的列表中作为这一层分治的最终结果
                for (Integer num:tempRes){
                    res.add(num);
                }
            }
        }
        return res;//这里容易漏掉
    }
//calculate函数用来对两个列表的数值逐个进行计算
    public static List<Integer> calculate(List<Integer> listOne,List<Integer> listTwo,char operator){
        List<Integer> res = new ArrayList<>();
        for (int i=0;i<listOne.size();i++){//一开始不明白这里为什么有两个循环，请看下面的例子就知道了
            for (int j=0;j<listTwo.size();j++){
                res.add(calculateTwoNums(listOne.get(i),listTwo.get(j),operator));
            }
        }
        return res;
    }
    //简单的计算函数
    public static Integer calculateTwoNums(int num1,int num2,char operator){
        switch(operator) {
            case '+':
                return num1+num2;
            case '-':
                return num1-num2;
            default:
                return num1*num2;
        }
    }
//判断是否当前表达式是否为一个数字
    public static boolean isOneNum(char[] expression){//把表达式都扫描一遍
        for (int i=0;i<expression.length;i++){
            if (!Character.isDigit(expression[i]))//只要发现有一个不是数字，就返回false，
                return false;
        }
        return true;//如果扫描完全部都是数字，就返回true
    }

}
1
2
3
4
5
6
7
System.arraycopy（）是一种本地静态方法，用于将元素从源数组复制到目标数组。
public static void arraycopy(Object src, int srcPos, Object dest, int destPos, int length)
Object src : 原数组
int srcPos : 从元数据的起始位置开始
Object dest : 目标数组
int destPos : 目标数组的开始起始位置
int length : 要copy的数组的长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
以"2*3-4*5"为例子，看看是如何计算的

第一轮情况
left and right
2    3-4*5
left and right
3    4*5
left and right
4    5

leftlist and rightlist
[4]    *    [5]
leftlist and rightlist
[3]    -    [20]

left and right
3-4    5
left and right
3    4

leftlist and rightlist
[3]    -    [4]
leftlist and rightlist
[-1]    *    [5]
leftlist and rightlist
[2]    *    [-17, -5]  //也就是(3-4)*5和3-(4*5)，这也解释了为什么calculate为什么是两个循环。第一和第二个结果出来了


第二轮情况
left and right
2*3    4*5
left and right
2    3

leftlist and rightlist
[2]    *    [3]

left and right
4    5

leftlist and rightlist
[4]    *    [5]
leftlist and rightlist
[6]    -    [20]   //第三个结果


第三轮情况
left and right
2*3-4    5
left and right
2    3-4
left and right
3    4

leftlist and rightlist
[3]    -    [4]
leftlist and rightlist
[2]    *    [-1]

left and right
2*3    4
left and right
2    3

leftlist and rightlist
[2]    *    [3]
leftlist and rightlist
[6]    -    [4]
leftlist and rightlist
[-2, 2]    *    [5]  //第四和第五个结果

答案为[-34, -10, -14, -10, 10]

932

312

代码随想录

代码随想录正式开刷！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
List<Integer> a = new ArrayList<>();
a.get(i)//获取第i个元素
a.size()
result.add(Arrays.asList(nums[i], nums[left], nums[right])) result是List<List<Integer>> 这样最后的结果类似于[[1,2,3],[2,3,4]]，也就是里面的List<Integer>省略，这个出现在15,18题

String s
s.charAt(i)


StringBuilder sb = new StringBuilder();
sb.toString()

Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
queue.offer(x)//添加x进去
queue.poll()//取出最后一个元素

HashMap<Integer, Integer> map = new HashMap<>();
map.put(key, value)
map.containsKey(key)//是否存在该元素

数组

704 二分查找 easy

前提是有序，以及没有重复的值，才可以用下面这个算法。
下面这个写法是左闭右闭区间，也就是target在这个区间内，所以必须要用小于等于。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while(left <= right) { //这里要注意是小于等于，比如我们用[5] target=5来举例，l和r都是0，这样就不会进入循环了，所以必须要小于等于。
            int  mid = left + ((right - left) / 2); //凡是取中间值，必须记住这个公式，如果直接(l+r)/2，可能会溢出。
            if (nums[mid] == target) return mid;
            else if (nums[mid] > target) {
                right = mid - 1;
            }
            else if (nums[mid] < target){
                left = mid + 1;
            }
        }
        return -1;
    }
}

27 移除元素 easy

注意数组只能覆盖掉哦，所以用到双指针的思路。数组的元素是不能删的，只能覆盖！数组的元素是不能删的，只能覆盖！数组的元素是不能删的，只能覆盖！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/*
这个题先考虑如果刚好第一个元素就是目标元素，我们应该怎么操作，这时候fast还在第一格，所以不能替换，那么就是先到下一个元素，再替换
那么，所以if应该设置为如果不是这个target的时候再操作
*/
class Solution {
    public int removeElement(int[] nums, int val) {
        int slow = 0;
        for (int fast = 0; fast < nums.length; fast++) {
            if (nums[fast] != val) {
                nums[slow] = nums[fast];
                slow++;
            }
        }
        return slow;
    }
}
/*
大概思路就是有两个指针，一个快指针一个慢指针
一开始的slow和fast指针都是0，直到遇上val后，这时候fast会比slow多跳一格，也就是slow还是不变，因为我们看代码，只有不等时，slow才会加
那么等到下一次不为val后，我们fast指向的值，就覆盖到之前val的位置上（因为slow指着呢），那么最后slow的指针，也就是最终的长度啦
所以这个题不要来想着怎么去移除元素，而是覆盖元素，运用双指针
*/

977 有序数组的平方 easy

这题给的数组是非递减数组，有负数，如果用暴力算平方然后排序时间复杂度很高，所以没有意思，下面用的是双指针的办法。本题用while的话

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/*
首先我们要知道，这是非递减数组，也就是平方之后的最大值，要么是第一个，要么是最后一个，所以可以用双指针的想法去做。
i指向第一个，j指向最后一个，然后判断谁的平方大，大的那个就存到result的最后一个位置，也就是倒着存。
如果是i情况，操作完把i++
如果是j情况，操作完把j--
同时n都要进行相减
因为i和j要看情况要相减，所以在for循环的时候我们发现第三栏空出来没有写了
*/
class Solution {
    public int[] sortedSquares(int[] nums) {
        int[] result = new int[nums.length];
        int n = nums.length - 1;//别忘了数组最后一个的位置是n-1，而不是n
        for (int i = 0,j = n; i <= j;) {//用小于等于是因为，当他们i和j共同指向这个数后，继续循环对这个数进行操作，不然用小于的话，到了这个数就不进行操作了。
            if ((nums[i] * nums[i]) > (nums[j]*nums[j])) {
                result[n--] = nums[i] * nums[i++];//注意前面一个不能i++，因为我们后面还要用到nums[i]
            } else {
                result[n--] = nums[j] * nums[j--];
            }
        }
        return result;
    }
}

while的写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int[] sortedSquares(int[] nums) {
        int[] result = new int[nums.length];
        int n = nums.length - 1;//别忘了数组最后一个的位置是n-1，而不是n
        int i = 0;
        int j = n;
        while(i <= j) {//用小于等于是因为，当他们i和j共同指向这个数后，继续循环对这个数进行操作，不然用小于的话，到了这个数就不进行操作了。
            if ((nums[i] * nums[i]) > (nums[j]*nums[j])) {
                result[n--] = nums[i] * nums[i++];//注意前面一个不能i++，因为我们后面还要用到nums[i]
            } else {//这里不能再用条件判断，不然会超时，指不用再判断<
                result[n--] = nums[j] * nums[j--];
            }
        }
        return result;
    }
}

209 长度最小的子数组 medium

注意是最小哦，举个例子，比如target=7，nums= [2,3,1,2,4,3],那么连续子数组[1,2,4]和[4,3]都符合，但是要取最小那个，也就是长度为2。本题有点类似于双指针，但是卡哥表达是滑动窗口。还有需要注意，题目是找出大于等于target的，一开始还看成等于的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/*
具体是这么理解的，两个指针，右指针一直走，这时候sum也在累加，一旦sum大于或者出现等于的情况，就把left右移动一位，同时别忘记删除原来的那个left的数字
可以用暴力，但是时间复杂度高，下面这个虽然有while，卡哥解释：不要以为for里放一个while就以为是O(n^2)啊， 主要是看每一个元素被操作的次数，每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)。
*/
class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int result = Integer.MAX_VALUE;
        int left = 0, sum = 0;
        for (int right = 0; right < nums.length; right++) {
            sum += nums[right];
            while (sum >= target) {//题目要求，加个while是为了寻找更小的长度
                result = Math.min(result, right - left + 1);//统计长度就是r-l+1
                sum -= nums[left++];//删除原来的left位置上的数字以及left++，如果移动一位还是大于，那就继续while移动，当然了，这时候right是不变的，因为我们还在for循环中
            }
        }
        return result == Integer.MAX_VALUE ? 0 : result;//如果result还是原来的max数，就说明找不到符合的条件，返回0，否则返回result
    }
}

59 螺旋矩阵2 medium

思路就是一圈圈循环，然后注意控制区间，本题答案是左闭右开写法，这题没涉及什么算法，就是繁琐。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    public int[][] generateMatrix(int n) {
        int start = 0;
        int loop = 0;//循环的圈数
        int i,j;//注意必须设置为全局变量
        int count = 1;//填入的数字，从1开始，一直到n*n
        int[][] res = new int[n][n];
        while (loop++ < n / 2) {//这里解释下为什么圈是是n/2，我们想想一个圈的内圈，会上下左右都少一格，也就是x少2，y少2，比如6，第一圈是x是6，第二圈就是4，第三圈就是2，这里代表元素个数，那么用6/2就是总圈数，遇到奇数下面会处理。
            //务必注意，进入循环后，loop的值就是1了，代表第loop圈
            //务必注意，进入循环后，loop的值就是1了，代表第loop圈
            //务必注意，进入循环后，loop的值就是1了，代表第loop圈
            for (j = start; j < n - loop; j++) {//左开右闭，所以用n-loop来控制，可以看下面卡哥的图就清楚了
                res[start][j] = count++;//模拟上侧从左到右
            }//只有这里是start，下面都是res[i][j]

            for (i = start; i < n - loop; i++) {//模拟右侧从上到下
                res[i][j] = count++;
            }
            //以3为例，第一圈循环到这里是时候,i和j都变成2了，loop是1，j进入循环内，j首先还是2

            //这里为什么要大于等于loop，我是这么想的，这时候处理右下角的数字，以4为例子，右下角坐标是(3,3)，目前是第一圈，左下角是(3,0),截止点是1(loop),第二圈的左下角是(2,1)，截止点是2(loop)，所以可以大于等于loop，循环完之后就不满足这个条件，就退出去了
            for (;j >= loop; j--) {// 模拟下侧从右到左
                res[i][j] = count++;
            }

            for (; i >= loop; i--) {// 模拟左侧从下到上
                res[i][j] = count++;
            }
            start++;//别忘了循环完一圈后，开始下一圈了，所以要改变起始点
        }
        if (n % 2 == 1) {//n为奇数的时候，最后会剩下一格，在while中是没有处理的
            res[start][start] = count;//当然了，也可以为n*n
        }
        return res;
    }
}

卡哥这个图很生动

链表

务必熟悉定义链表

1
2
3
4
5
6
7
8
9
public class ListNode {
    int val;
    ListNode next;
    ListNode() {};//{}容易漏
    ListNode(int val, ListNode next) {
        this.next = next;
        this.val = val;
    }
}
1
2
3
4
5
6
7
8
9
一些总结：
cur一般指向head，pre一般指向null，如果有虚拟节点，就指向dump，这样保证了head（cur的指向）之前是pre
203：移除元素需要设置虚拟节点，pre和cur，循环的时候while（cur！=null），那么为什么不是cur.next！=null呢，因为如果你现在到最后一个元素，next必然是空，那么这时候就不会循环，但是如果最后一个元素就是目标val，需要进行操作，而不会进入到循环中
另外，如果一直遇到val，pre不变位置，而是一直指向cur的next，然后cur一直移动

206:对应反转链表，虚拟节点不好操作，因为你最后要反的，但是pre和cur是要的，pre的话这里没有dump，就先设置为null
19:删除倒数第n个节点，虚拟节点的设置，以及fast和slow需要初试化在dump上而不是head上，因为可能[1]1，如果这样的话，一开始在节点上就不能操作，所以都设置在head的前面
另外，循环是用fast.next!=null，如果是这样，fast最后是在最后一个元素上，如果直接用fast，则会在null元素上。然后slow会在需要删除节点的前面一个位置，最后进行改变指针即可

203 移除链表元素 easy

这个是带虚拟头节点的，方便操作,然后设置一个pre和cur指针，如果cur遇到val，就修改pre的next指向，否则pre指向cur，然后cur一直移动。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        if (head == null) {
            return head;
        }
        ListNode dump = new ListNode(0);
        dump.next = head;
        ListNode pre = dump;
        ListNode cur = pre.next;
        while (cur != null) {
            if (cur.val == val) {
                pre.next = cur.next;
            } else {
                pre = cur;
            }
            cur = cur.next;
        }
        return dump.next;
    }
}

注意下如何声明链表，因为可能是ACM模式，本解答是在原链表上进行移除，也就是不带虚拟头节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;//下一个节点
 *     ListNode() {}// 节点的构造函数(无参)
 *     ListNode(int val) { this.val = val; }// 节点的构造函数(有一个参数)
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }// 节点的构造函数(有两个参数)
 * }
 */
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        while (head != null && head.val == val) {
            head = head.next;
        }//当头节点就是目标时，直接把head移动到下一个即可，用while是因为可能遇到[7,7,7] val=7这种情况，就需要一直移动

         if (head == null) {//当head为空的时，就直接返回null，但是这一句不能写在上面一句之前，比如还是上面那个例子，while后会变成空，然后到了这句就直接返回null，但是如果先写这一句，while执行完后却不会返回null
            return null;
        }  

       //当val不是头节点的时候
        ListNode pre = head;//声明pre和cur
        ListNode cur = pre.next;

        while (cur != null) {
            if (cur.val == val) {//当cur为目标时候，把pre的next直接指向cur的next即可
                pre.next = cur.next;
            } else {
                pre = cur;//不是目标的时候，继续走下一个元素
            }
            cur = cur.next;
        }
        return head;
    }
}

707 设计链表 medium

本答案的链表设计是有虚拟头节点的，这样是为了所有节点可以用一样的操作，不然要分为头节点和其他节点，使用单链表，这个题比较容易漏掉size的数值变化增长。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
//这里的index起始是0，，也就是我们插入的节点位置就是他的下标位置，所以最大的index是size-1
class ListNode {
    int val;
    ListNode next;
    ListNode() {};
    ListNode(int val) {
        this.val = val;
    }
    ListNode(int val, ListNode next) {//题目不需要这个也行，但是我为了练习多写的
        this.val = val;
        this.next = next;
    }
}
class MyLinkedList {
    int size;
    ListNode head;//务必注意head是全局变量哦
    public MyLinkedList() {
        size = 0;
        head = new ListNode(0);

    }
    
    public int get(int index) {
        if (index < 0 || index >= size) {//获取index必须要在size的范围内
            return -1;
        }
        ListNode currentNode = head;
        for (int i = 0; i <= index; i++) {//因为我们有一个虚拟头节点，所以要<=index，只有getindex的情况才这样哦，add和delete都不需要
            currentNode = currentNode.next;
        }
        return currentNode.val;//返回的值哦
    }
    
    public void addAtHead(int val) {

        addAtIndex(0, val);
    }
    
    public void addAtTail(int val) {
        addAtIndex(size, val);

    }
    
    public void addAtIndex(int index, int val) {
        if (index > size) {
            return;
        }
        if (index < 0) {//本题的要求，输入负数则在头部插入
            index = 0;
        }
        size ++;//这个比较容易漏
        ListNode pred = head;//找到要插入节点的前驱

        for (int i = 0; i < index; i++) {
            pred = pred.next;
        }
        ListNode toAdd = new ListNode(val);

        //先让新增的点连接后面，再连接前面。
        toAdd.next = pred.next;//不能和下面一句顺序反过来，不然toAdd的next就断掉了
        pred.next = toAdd;


    }
    
    public void deleteAtIndex(int index) {
        if (index < 0 || index >= size) {
            return;
        }
        size--;//这个比较容易漏
        ListNode pred = head;
        for (int i = 0; i < index; i++) {
            pred = pred.next;
        } 
        pred.next = pred.next.next;
    }
}

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * MyLinkedList obj = new MyLinkedList();
 * int param_1 = obj.get(index);
 * obj.addAtHead(val);
 * obj.addAtTail(val);
 * obj.addAtIndex(index,val);
 * obj.deleteAtIndex(index);
 */
1
2
3
4
这里之前有个疑问，为什么每次操作链表都要先声明一个listnode？
ListNode currentNode = head;
这样操作的话是cur在动，而head没有动
假设你直接用head操作，这样你第一次getindex是可以的，但是第二次getindex的话，head的位置早就变了。

206 反转链表 easy

直接在链表的基础上进行反转，也就是改变next的指向，让其反过来，思路就是设置一个pre和cur，然后用temp保存cur的next，再把cur反转到pre。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre = null;
        ListNode cur = head;
        ListNode temp = null;//需要有个temp来保存cur的next指针

        while (cur != null) {//如果cur.next ！= null 会少了设置最后一个节点
            temp = cur.next;//先保存
            cur.next = pre;//指向调转
            pre = cur;//继续移动
            cur = temp;//继续移动
        }
        return pre;
    }
}

24 两两交换链表中的节点 meduim

这个题用了虚拟节点，必须要画图，这样才好理解，定义pre和cur，以两个为一组操作，然后先保存下一组的第一个数，接着操作第一组，改变指针指向。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode dump = new ListNode(0);
        dump.next = head;
        ListNode temp = null;
        ListNode pre = dump;
        ListNode cur = head;
        while (cur != null && cur.next != null) {//保证有两个节点
            temp = cur.next.next;
            pre.next = cur.next;
            pre.next.next = cur;
            cur.next = temp;
            pre = cur;
            cur = cur.next;
        }
        return dump.next;
    }
}


和上一个解答的区别是，这个直接用head代替cur，但是一般我们都是用一个新的cur来写，所以我感觉上面一个风格更适合我。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode dump = new ListNode(0);
        dump.next = head;
        ListNode pre = dump;
        while (pre.next != null && pre.next.next != null) {
            ListNode temp = head.next.next;//先保存一下节点
            pre.next = head.next;//对应步骤一
            pre.next.next = head;//对应步骤二
            head.next = temp;//对应步骤三
            pre = head;//移动一位
            head = head.next;//移动一位
        }
        return dump.next;//注意dump是虚拟节点，所以是dump的next
    }
}

19 删除链表的倒数第 N 个结点 medium

这个题一开始想不通怎么去处理倒数这个条件。这就用到了双指针啦，也就是先让fast先跑n步（卡哥说n+1但是我计算后觉得还是n），然后slow和fast同时跑，直到fast移动到末尾（是null哦，不是最后一个元素，也就是最后一个元素的下一个），这时候slow的指向就是待删除的元素，那么在跑的时候，我们再定义一个pre，就可以删除slow元素了。
第二次做这个题意识到，这个必须要用一个虚拟节点，不然很难处理[1]1这个情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dump = new ListNode(0);
        dump.next = head;
        ListNode slow = dump;
        ListNode fast = dump;

         
         
        /*for (int i = 0; i < n; i++) {
            fast = fast.next;
        }*/
        while (n-- > 0) {
            fast = fast.next;
        }//上面两种写法都可以


        ListNode pre = null;//用于保存slow的前面一个元素，方便删除
        while (fast != null) {
            pre = slow;//这个必须写第一个顺序，不能写在后面。
            fast = fast.next;
            slow = slow.next;

        }
        pre.next = slow.next;//slow指向的元素就是我们需要删除的
        return dump.next;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dump = new ListNode(0);
        dump.next = head;

        ListNode slow = dump;
        ListNode fast = dump;

        while(n-- > 0) {
            fast = fast.next;
        }

        while (fast.next != null) {//和上面题解的区别
            slow = slow.next;
            fast = fast.next;
        }

        slow.next = slow.next.next;//和上面题解的区别
        return dump.next;
    }
}

面试题 02.07. 链表相交 easy 同160题

题目链接，这个题需要注意交点不是数值相等，而是指针相等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
/*
总体的思路就是定义两个cur，首先是计算他们的长度，然后把长的一个链表放前面，如curA，然后把他们尾部对齐，接着寻找相同的指针即可。
需要注意的是，计算完长度后，请马上让cur重新指向头。
*/
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode curA = headA;
        ListNode curB = headB;
        int lenA = 0, lenB = 0;
        while (curA != null) {
            curA = curA.next;
            lenA++;
        }
        while (curB != null) {
            curB = curB.next;
            lenB++;
        }
        curA = headA;
        curB = headB;//这里很关键，计算完长度请马上指向头

        //让curA保持为最长那个，这样方便操作，所以如果B的更长，那就交换一下
        if (lenB > lenA) {
            int temp = lenA;
            lenA = lenB;
            lenB = temp;
            ListNode tem = curA;//不能重复用temp
            curA = curB;
            curB = tem; 
        }
        //这个操作的目的是，让curA移动到和curB对齐的地方
        int gap = lenA - lenB;
        while (gap-- > 0) {
            curA = curA.next;
        }        
        while (curA != null) {
            if (curA == curB) {//这里不能写成curA.val == curB.val，但是可以通过不少例子，下面举一个例子说明为什么不可以
                return curA;
            }
            curA = curA.next;
            curB = curB.next;
        }
        return null;//这个不能忘了
    }
}
1
2
3
4
5
6
7
8
9
10
8
[4,1,8,4,5]
[5,0,1,8,4,5]
2
3

上面的输入，对齐后是
[5,0,1,8,4,5]
  [4,1,8,4,5]
根据输入，完美可以知道应该是返回8这个节点，但是如果我们用了curA.val == curB.val，则会返回1，这个是错误的

卡哥的图，主要理解curA移动到和curB对齐的地方这个操作

环形链表

141 环形链表 easy

判断一个链表是否有环，很简单，设置快慢指针，如果最终快指针追上慢指针，说明有环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                return true;
            }
        }
        return false;
    }
}

142 环形链表II medium

之前做过又忘记！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                ListNode index1 = fast;
                ListNode index2 = head;//第二次写这个题，居然写成slow
                while (index1 != index2) {
                    index1 = index1.next;
                    index2 = index2.next;
                }
            return index1;//也可以返回2
            }
        }
        return null;//第二次做这个题忘记返回null
    }
}

卡哥的详细解释

1
2
3
4
5
6
7
8
9
10
11
12
卡哥的答案确实比较详细，这里简单总结下
一个快指针，一个慢指针，快指针走两步，慢指针走一步。
这样子，其实快指针是在慢慢一步步靠近慢指针，如果有环的话，一定会相遇。
当他们相遇的时候，这时候我们重新声明两个指针，一个指向fast，一个指向头，然后他们一步步走，最终相遇的时候，就是入口，这里面涉及一些公式推导，去卡哥网站上看吧。


这里解释下卡哥这句话
那么fast指针走到环入口3的时候，已经走了k + n 个节点，slow相应的应该走了(k + n) / 2 个节点。
因为k是小于n的（图中可以看出），所以(k + n) / 2 一定小于n

(n + n) / 2 = n ，k < n，所以(k + n) / 2 一定小于n。
也就是说你的fast已经走到了环入口三，而slow还没走到环入口三，并且一开始fast在环入口2的前面，也就是他们已经相遇过了。

哈希表

242 有效的字母异位词 easy

若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/*
用一个26长度是int数组来记录s的字母个数
然后用t的字母减去相应个数
最后如果发现record数组都是0，那证明就是异味词，否则不是
String中用s.toCharArray
*/
class Solution {
    public boolean isAnagram(String s, String t) {
        int[] record = new int[26];
        for (char c:s.toCharArray()) {
            record[c - 'a'] += 1;//toCharArray将字符串转换为字符数组，比如单独输出a 然后a - 'a' = 0,那么在0的位置上加1，b的话就在1的位置上加1
        }

        for (char c:t.toCharArray()) {
            record[c - 'a'] -= 1;
        }
        /*for (int i = 0; i < 26; i++) {
            if (record[i] != 0 ) {
                return false;
            }
        }*/

        //下面这个写法更简洁
        for (int i : record) {
            if (i != 0) {
                return false;
            }
        }
        return true;        
    }
}

349 两个数组的交集 easy
set可以去重，通过两个set就可以找到交集。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        Set<Integer> set1 = new HashSet<>();
        Set<Integer> set2 = new HashSet<>();
        for (int i : nums1) {
            set1.add(i);
        }

        for (int i : nums2) {
            if (set1.contains(i)) {
                set2.add(i);
            }
        }
        int[] result = new int[set2.size()];
        int index = 0;
        for (int i : set2) {//把结果转成数组
            result[index++] = i;
        }
        return result;
    }
}

202 快乐数 easy
这个题其实就是按照题目思路去走即可，需要知道如何拆出数字来获取，比如个位数用mod，然后其他位置依次循环除以10。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public boolean isHappy(int n) {
        Set<Integer> result = new HashSet<>();//这个题的求和过程中可能会有数字重复出现，所以要用hash的set去重
        while (n != 1 && !result.contains(n)) {
            result.add(n);
            n = getnextnum(n);
        }
        return n == 1;

    }
    private int getnextnum(int n) {//比如19
        int sum = 0;
        while (n > 0) {
            int temp = n % 10;//先获得9
            sum += temp * temp;//81
            n = n / 10;//然后获得1
        }
        return sum;
    }
}

1 两数之和 easy

一开始就行想着暴力解法，虽然过了，用了两个循环，但是看了卡哥的解释还是太年轻了,这里有个细节，一定要先判断，然后再put元素进去，否则遇到[3,3] targer=6 这种情况，res答案就会变成[1,1]，而不是[0,1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/*
这里只用了一个循环就可以完成这个任务，用到了map
map<key,value>
放到这个题就是key存nums[i]，value存位置信息。
一开始是存前面的数和位置，到了后面target相减后，如果在map中有匹配的数，那就说明已经找到符合题目的数了。
*/
class Solution {
    public int[] twoSum(int[] nums, int target) {
        int[] result = new int[2];
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int temp = target -nums[i];//相减后的数
            if (map.containsKey(temp)) {//如果相减后的数在map中，就说明成功了
                result[0] = i;
                result[1] = map.get(temp);
            }
            map.put(nums[i], i);
        }
        return result;
    }
}

454 四数相加2 medium

第一次看到这么巧妙的做法，看来还是练题太少了。这个题不用考虑重复的四个元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/*
这个题用到了map来保存前两个数的和以及出现的次数，然后后面两个数用0去相减他们的和得到一个值，
如果这个值在map中存在，那就提取次数，最后累加次数就是答案。
这里一开始不明白为什么用map来保留次数，比如前两个数组是[1,1],[1,1]，那么map中就是(2:4)，也就是和为2的有4个，至于是什么组合我们不用管
因为题目只需要知道最后有多少次
*/
class Solution {
    public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        Map<Integer, Integer> map = new HashMap<>();
        int temp = 0, res = 0;
        for (int i :nums1) {
            for (int j : nums2) {
                temp = i + j;
                if (map.containsKey(temp)) {
                    map.put(temp, map.get(temp) + 1);
                } else {
                    map.put(temp, 1);
                }
            }
        }

        for (int i : nums3) {
            for (int j : nums4) {
                temp = i + j;
                if (map.containsKey(0 - temp)) {
                    res += map.get(0 - temp);
                }
            }
        }
        return res;
    }
}

让语句写更少一些，主要在map的修改上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        int res = 0;
        int temp;
        Map<Integer, Integer> map = new HashMap<>();
        for (int i : nums1) {
            for (int j : nums2) {
                temp = i + j;
                map.put(temp, map.getOrDefault(temp, 0) + 1);
            }
        }

        for (int i : nums3) {
            for (int j : nums4) {
                temp = i + j;
                if (map.containsKey(0 - temp)) {
                    res += map.get(0 - temp);
                }
            }
        }
        return res;        
    }
}

383 赎金信 easy

一开始想得挺复杂，看到卡哥提点都是小写字母，可以用一个26大小的char数组保存这句话，就写出来了，没想到和卡哥答案一样，嘻嘻。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public boolean canConstruct(String ransomNote, String magazine) {
        int[] result = new int[26];
        for (char i : magazine.toCharArray()) {//注意题目是后者的个数要覆盖前者的个数哦，所以先提取magazine
            result[i - 'a'] += 1; 
        }

        for (char i : ransomNote.toCharArray()) {
            result[i - 'a'] -= 1;
        }
        for (int i : result) {
            if(i < 0 ) {
                return false;
            }
        }
        return true;

    }
}

15 三数之和 medium(非哈希法)

哈希法太复杂，这里是双指针，而且和454的区别是，454是4个数组，这个题是一个数组，而且不能是重复的三元组，这个题要多看看，可能第二遍又忘记了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/*
这个题用双指针更加方便
不过一开始是指向i,left,right
left的初始化是i+1
这里有个关键是，必须先进行排序。
学习Arrays.asList
记不住就
                    List<Integer> res = new ArrayList<>();
                    res.add(nums[i]);
                    res.add(nums[left]);
                    res.add(nums[right]);
                    result.add(res);
*/
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums);

        for (int i = 0; i < nums.length; i++) {
            if (nums[i] > 0) {//因为已经排序了，如果第一个就大于0，那后面就不可能和为0了
                return result;//这个题我试了下，用nums[0]也可以，不过要放在for内，如果在sort下面写nums[0] > 0判断，可能不行，因为用例可以是空的[]，这样就没有nums[0]。
            }
            if (i > 0 && nums[i] == nums[i - 1]) {//加个大于0，是因为怕一开始的情况，0-1=-1就不成立啦
                continue;
            }//去重操作，不能直接写成nums[i] == nums[i + 1]，因为会漏掉比如-1,-1,2这种情况，也就是一开始就筛掉了

            int left = i + 1;
            int right = nums.length - 1;
            while (right > left) {
                int sum = nums[i] + nums[left] + nums[right];
                //不可以在这里写去重条件，也就是最下面else那个，如果这里写的话，万一用例是0,0,0，那么就直接筛掉了，而在下面写，是为了保证已经添加了元祖，再进行去重。
                if (sum > 0) {
                    right--;
                } else if (sum < 0) {
                    left++;
                } else {
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));//添加元祖，然后再去重

                    //去重条件，注意righ-1，下面是left + 1
                    while (right > left && nums[right] == nums[right - 1]) right--;
                    while (right > left && nums[left] == nums[left + 1]) left++;   //注意这里是left+1            
                    right--;
                    left++;

                }
            }
        }
        return result;
    }
}

18 四数之和 medium

和上一题的区别是，这个是四元组，而且和不是为0，是任意值target。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/*
具体的区别有，首先不再判断第一个数大于0就continue，因为这个题是任意值。
只需要多加一个for循环，再多一个j，同理如果是5元组，6元组也如此。
*/
class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums);
       
        for (int i = 0; i < nums.length; i++) {

            if (i > 0 && nums[i - 1] == nums[i]) {//i要去重
                continue;
            }
            
            for (int j = i + 1; j < nums.length; j++) {

                if (j > i + 1 && nums[j - 1] == nums[j]) {
                    continue;
                }//多加一个循环，同时这里需要去重，j也要去重。

                int left = j + 1;
                int right = nums.length - 1;
                while (right > left) {
                    long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];//因为这个题是任意值，所以用例有个越界的，转成long。
                    if (sum > target) {
                        right--;
                    } else if (sum < target) {
                        left++;
                    } else {
                        result.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
                        
                        while (right > left && nums[right] == nums[right - 1]) right--;
                        while (right > left && nums[left] == nums[left + 1]) left++;

                        left++;
                        right--;
                    }
                }
            }
        }
        return result;
    }
}

字符串

344 反转字符串 easy

简简单单。

1
2
3
4
5
6
7
8
9
10
class Solution {
    public void reverseString(char[] s) {
        char temp;
        for (int i = 0; i < s.length / 2; i++) {
            temp = s[i];
            s[i] = s[s.length - 1 -i];
            s[s.length - 1 - i] = temp;
        }
    }
}

一样的效果，只是一个for，一个是用while。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public void reverseString(char[] s) {
        char temp;
        int left = 0, right = s.length - 1;
        while (left < right) {
            temp = s[left];
            s[left] = s[right];
            s[right] = temp;
            left++;
            right--;
        }
    }
}

541 反转字符串2 easy

比较繁琐，需要定义判断多种情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/*
每2k长度进行一次操作，也就是固定一段去处理字符串。
这里题目要求，剩余长度大于少于k，则全部反转，剩余长度小于2k，则反转前k个，所以可以i+k去处理
*/
class Solution {
    public String reverseStr(String s, int k) {
        int n = s.length();
        char[] arr = s.toCharArray();
        for (int i = 0; i < n; i += k * 2) {//每隔2k来处理，然后找到起点
            reverse(arr, i, Math.min(i + k, n) - 1);//这里用min是怕越界，如果直接用if判断i+k < n又会漏了一些情况，秒！
        }
        return new String(arr);

    }
    public void reverse(char[] arr, int left, int right) {
        while (left < right) {
            char temp = arr[left];
            arr[left] = arr[right];
            arr[right] = temp;
            left++;
            right--;
        }            
    }
}

剑指 Offer 05. 替换空格 easy

题目链接，一开始想法的替换空格，但是忘记一个事，%20是三个字符，所以要申请空间，干脆用SrtingBuilder。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/*
其实return s.replace(" ","%20");即可，但是这是算法题哦
*/
class Solution {
    public String replaceSpace(String s) {
        //第一次用StringBuilder，最后要转成String，也就是直接复制原来s到StringBuilder中
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i <  s.length(); i++) {
            if (s.charAt(i) == ' ') {
                sb.append("%20");
            } else {
                sb.append(s.charAt(i));
            }
        }
        return sb.toString();
    }
}

151 颠倒字符串中的单词 medium

这个题比较多繁琐的东西，下面详细讲。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    public String reverseWords(String s) {
        StringBuilder sb = RemoveSpace(s);
        ReverseString(sb, 0, sb.length() - 1);
        ReverseEachWords(sb);
        return sb.toString();
    }

    public StringBuilder RemoveSpace(String s) {
        int start = 0, end = s.length() - 1;
        while (s.charAt(start) == ' ') start++;
        while (s.charAt(end) == ' ') end--;
        StringBuilder sb = new StringBuilder();
        while (start <= end) {
            char c = s.charAt(start);
            if (c != ' ' || sb.charAt(sb.length() - 1) != ' ') {
                sb.append(c);
            }
            start++;
        }
        return sb;
    }

    public void ReverseString(StringBuilder sb, int start, int end) {
        while (start < end) {
            char temp = sb.charAt(start);
            sb.setCharAt(start, sb.charAt(end));
            sb.setCharAt(end, temp);
            start++;
            end--;
        }
    }

    public void ReverseEachWords(StringBuilder sb) {
        int start = 0;
        int end = 1;
        int n = sb.length();
        while (start < n) {
            while (end < n && sb.charAt(end) != ' ') {
                end++;
            }
            ReverseString(sb, start, end - 1);
            start = end + 1;
            end = start + 1;
        }

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
总体思路是
1.去除多余的空格
比如[ the     sky   ]，去除后是[the sky]，要去掉多余的两边空格，以及中间只需要保留一个空格。
函数里面while (start <= end)，这里有个等于号，如果没有的话，会漏掉最后一个字符，因为我们是用start去提取字符，自然start要到最后
重点看if (c != ' ' || sb.charAt(sb.length() - 1) != ' ')
这句前面部分，是为了保证非空格元素添加进去，而后面则是为了去除两个单词之间多余的空格
举个例子[the  sky]，中间有两个空格，start为4的时候，为第一个空格，此时sb是the，如果看前面第一个条件，是不允许添加的，但是这个是或，后面那个条件sb提取出来的是e，所以，这时候位置4的空格可以添加进去，
这时候sb是[the ]，然后开始第五个位置，同样，前面第一个条件不通过，第二个条件也不通过，因为此时sb最后一个字符是空格，这样的话，两个单词之间，就可以做到保留一个空格


2.翻转字符串
这个没啥好说的，就是字面意思

3.翻转单词
这个就有意思了，我们检测到空格位置，就说明检测完一个单词，然后再把这个单词放进翻转字符串，即可完成，这里别忘了，翻转字符串的end是位置，不是长度，
所以ReverseString(sb, start, end - 1);这个容易漏掉end-1

剑指 Offer 58 - II. 左旋转字符串 easy

题目链接，感觉卡哥写的还复杂。

1
2
3
4
5
6
7
8
9
10
11
12
13
//自己写的，感觉还行，后来看了下官方题解，居然一样！
class Solution {
    public String reverseLeftWords(String s, int n) {
        StringBuilder sb = new StringBuilder();
        for (int i = n; i < s.length(); i++) {
            sb.append(s.charAt(i));
        }
        for (int i = 0; i < n; i++) {
            sb.append(s.charAt(i));
        }
        return sb.toString();
    }
}

28 实现 strStr() easy(KMP)

别看是easy题，这是KMP算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
KMP算法的目的就是解决字符串匹配，其实挺神奇的，不过具体的数学原理是啥，有点懵，先把一些概念解释清楚
首先理解前缀和后缀，以及前缀表
以要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf这个为例子。
我们要构建模式串(needle)的前缀表。
1.前缀的理解，概念是指不包含最后一个字符的所有以第一个字符开头的连续子串
a
aa
aab
aaba
aabaa
上面五个都是前缀，不包含最后一个字符哦
2.后缀的理解，指不包含第一个字符的所有以最后一个字符结尾的连续子串。
f
af
aaf
baaf
abaaf
上面五个都是后缀，不包含第一个字符哦
3.前缀表，也就是最长相等前后缀（均用不减1的操作，有些KMP的next数组用减1）。
a 0
aa 1  这里前缀a，后缀a，相等的长度就是1
aab 0
aaba 1 只有前缀a和后缀a相等
aabaa 2 前缀aa和后缀aa相等
aabaaf 0
0 1 0 1 2 0就是我们模式串的前缀表。

再举一个例子asdfasdfasdf
next表是[0, 0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8]
前缀asdfasdf
后缀asdfasdf
也就是前缀和后缀是有重叠位置的时候
所以这里是强化下我们的概念，前缀是不包含最后一个字符，后缀是不包含第一个字符，所以他们即便是重叠的，都没关系，我们重点关注的是概念！




大致的解题思路是
1.首先构建好前缀表
2.循环文本串，然后循环匹配，如果不匹配，则寻找之前匹配的位置，如果匹配，j++，最后如果出现了文本串则根据题目要求返回相应值。

下面这个图很好解释了为什么当我们遇到不匹配的字符后，因为next数组记录了相等前后缀长度，遇到不匹配的字符后，j回退到next[j-1]，这个next[j-1]就是他们之前的最长相等前后缀长度，也就是回退到这个位置的时候，模式串从0到这个位置的字符，是和主串i位置之前的字符相等，之前字符的长度，就是模式串从0到这个位置的字符的长度，这是核心理解。至于next数组为什么那么求，目前还没有深刻的理解，但是至少理解了，为什么要回退这个步骤。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    public int strStr(String haystack, String needle) {
        int[] next = new int[needle.length()];
        int j = 0;
        getNext(next, needle);
        for (int i = 0; i < haystack.length(); i++) {//这里是从0开始的哦
            while (j > 0 && needle.charAt(j) != haystack.charAt(i)) {
                j = next[j - 1];
            }
            if (haystack.charAt(i) == needle.charAt(j)) {
                j++;
            }
            if (j == needle.length()) {
                return i  - needle.length() + 1;//因为我们是要找主串上的起始位置，所以 是用i去减，而不是j
            }
        }
        return -1;

    }
    private void getNext(int[] next, String s) {
        int j = 0;
        next[0] = 0;//这句可写可不写，因为初始化的时候都是0
        for (int i = 1; i < s.length(); i++) {//i是从1开是的，因为你只有一个字母的时候，肯定是0，所以第一个不用考虑，直接从第二个位置开始
            while (j > 0 && s.charAt(i) != s.charAt(j)){
                j = next[j - 1];
            }
            if (s.charAt(i) == s.charAt(j)) {
                j++;
            }
            next[i] = j;
        }

    }
}

459 重复的子字符串 easy(KMP)

重点理解周期长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public boolean repeatedSubstringPattern(String s) {
        int n = s.length();
        if (n == 0) return false;
        int[] next = new int[s.length()];
        getNext(next, s);

        if (n % (n - next[n - 1]) == 0 && next[n - 1] != 0) {
            return true;
        }
        return false;


    }
    public void getNext(int[] next, String s) {
        int j = 0;
        for (int i = 1; i < s.length(); i++) {
            while(j > 0 && s.charAt(i) != s.charAt(j)) j = next[j - 1];
            if (s.charAt(i) == s.charAt(j)) j++;
            next[i] = j;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
这个题也是kmp的题目，寻找重复的子串
注意理解一个概念：
数组长度减去最长相同前后缀的长度相当于是第一个周期的长度，也就是一个周期的长度，如果这个周期可以被整除，就说明整个数组就是这个周期的循环。
所以我们求完next数组后
n % (n - next[n - 1]) == 0 n是长度，next[n - 1]也就是最长的相同前后缀的长度
next[n - 1] != 0这个是为了保证，next数组最后一个长度不是0，否则判断出错，下面举个例子

"abac"的next数组是[0, 0, 1, 0]，如果没有next[n - 1] != 0这个条件，那就是4 % (4 - 0) == 0就返回了true，实际上是false，所以要保证最长相同前后缀长度不为0先


"aaaa"的next数组是[0,1,2,3]，那么4 %(4 - 3) ==0返回true，4-3=1也就是说这个周期长度是1

栈与队列

232 用栈实现队列 easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class MyQueue {
    Stack<Integer> Stackin;//首先全局定义
    Stack<Integer> Stackout;

    public MyQueue() {
        Stackin = new Stack<>();//别忘了new
        Stackout = new Stack<>();
    }
    
    public void push(int x) {
        Stackin.push(x);
    }
    
    public int pop() {
        dumpStackin();
        return Stackout.pop();
    }
    
    public int peek() {
        dumpStackin();
        return Stackout.peek();
    }
    
    public boolean empty() {
        return Stackin.isEmpty() && Stackout.isEmpty();

    }
    public void dumpStackin() {
        if (!Stackout.isEmpty()) return;//先检查出栈，如果出栈不为空，则直接使用出栈队列，也就是返回一个号空
        while (!Stackin.isEmpty()) {//如果入栈不为空，要把入栈的全部移动到出栈，注意入栈此时要删除元素
            Stackout.push(Stackin.pop());
        }
    }
}

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * boolean param_4 = obj.empty();
 */
1
2
3
4
5
6
7
8
9
10
11
12
这个题是用两个栈来实现队列的操作
队列：先进先出 栈：先进后出
pop：移除元素并返回该元素
peak：返回队列开头元素
push：添加元素
那么用栈去完成队列的功能，需要两个栈，一个为作为入栈，一个作为出栈。

入栈：直接就是push元素进去
pop：检查出栈有无元素，有的话直接操作出栈的元素，如果出栈是空的话，那么将入栈的目前所有的元素全部移动到出栈中，再操作出栈pop
peak：和pop一样的道理
pip和peak都是java内置的，所以直接调用，我们主要是负责把入栈的元素移动到出栈中，这样才可以实现队列先进先出的功能
那么判断栈是否为空，只要两个都是空，那么就是空栈

225 用队列实现栈 easy

题目要求必须要用两个队列
pop移除并返回栈顶元素
top返回栈顶元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/*
关于LinkedList一些api
peekFirst()此方法用于检索链表的第一个元素，初始元素或开始元素，但不会从列表中删除第一个元素。
peekLast()方法用于返回此双端队列表示的队列的最后一个元素，但不删除该元素。
pollLast()检索并删除此列表的最后一个元素，如果此列表为空，则返回null。
pollFirst()检索并删除此列表的第一个元素，如果此列表为空，则返回null。

可以用queue，也可以用deque
用了两个deque，核心在pop上，弹出元素的时候，思路就是先把que1除了最后一个元素，然后将其他元素全部移到que2中
这时候que1只剩下一个元素，这个元素就是需要的值，然后再将que2变成que1即可。
*/
class MyStack {
    Deque<Integer> que1;
    Deque<Integer> que2;
    public MyStack() {
        que1 = new ArrayDeque<>();
        que2 = new ArrayDeque<>();

    }
    
    public void push(int x) {
        que1.addLast(x);

    }
    
    public int pop() {
        int n = que1.size();
        n--;//除了最后一个元素，其余元素都要移到que2中
        while (n-- > 0) {
            que2.addLast(que1.peekFirst());
            que1.pollFirst();
        }
        int res = que1.pollFirst();
        que1 = que2;
        que2 = new ArrayDeque();

        return res;
    }
    
    public int top() {
        return que1.peekLast();
    }
    
    public boolean empty() {
        return que1.isEmpty();

    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

下面是用双端队列，抖机灵用的，只用一个队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class MyStack {
    Deque<Integer> que;//双端队列

    public MyStack() {
        que = new ArrayDeque<>();

    }
    
    public void push(int x) {
        que.addLast(x);

    }
    
    public int pop() {//栈顶：最后一个入栈的元素
        int res = que.pollLast();//栈的是先进后出，队列是先进先出，所以从队列最后返回也就是对应栈的先进后出
        return res;
    }
    
    public int top() {
        return que.peekLast();//和上面一样的道理，只不过不需要删除元素
    }
    
    public boolean empty() {
        return que.isEmpty();

    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

20 有效的括号 easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/*
定义一个栈（其实双端队列也行）
然后扫描字符串s，如果是(,就在栈中放)，如果是[，就在栈中放]，如果是{，就在栈中放}。
然后如果扫描到),],}如果这时候的栈顶是该元素，就删除，如果不是，说明不匹配了，直接返回false，还有一种情况是，栈是空的，也是不匹配的情况
最后检查栈是不是为空，为空就说明全部匹配上了
*/
class Solution {
    public boolean isValid(String s) {
        Stack<Character> que = new Stack<>();
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '(') {
                que.push(')');
            } else if (s.charAt(i) == '[') {
                que.push(']');
            } else if (s.charAt(i) == '{') {
                que.push('}');
            } else if (que.isEmpty() || que.peek() != s.charAt(i)) {
                return false;
            } else if (que.peek() == s.charAt(i)) {
                que.pop();
            }
        }
        return que.isEmpty();
    }
}

1047 删除字符串中的所有相邻重复项 easy

这个可以看卡哥的动画，瞬间就可以明白

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/*
定义一个双端队列
如果队列是空的或者队列的顶元素和当前s[i]不一样，就把s[i]押进队列中，
如果当前s[i]和顶元素一样的话，就删除该队列中该元素，这也就是"对对碰消失"的核心
最后就是把里面的元素提取出来整合到字符串中
*/
class Solution {
    public String removeDuplicates(String s) {
        ArrayDeque<Character> que = new ArrayDeque<>();
        for (int i = 0; i < s.length(); i++) {
            char ch = s.charAt(i);
            if (que.isEmpty() || que.peek() != ch) {
                que.push(ch);
            } else {
                que.pop();
            }
        }
        String result = "";
        //队列最后是[a,c]的话，首先弹出c,然后再弹出a，所以pop后加上result才能正确拼接
        while (!que.isEmpty()) {
            result = que.pop() + result;//有个不留意的地方，第一次写成result += que.pop()； 相当于result = result + que.pop()，这是错误的，加错了。
        }
        return result;
    }
}

150 逆波兰表达式求值 medium

这个题看动画就秒懂了，这个是后缀表达式，可以依次顺序来计算结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/*
一个小知识点： ""是String类型，''是char类型
思路就是，如果检测到有符号，就说明需要运算，就弹出之前的两个值进行运行，然后再把结果push到队列中即可。
但是注意先弹出的元素是后运算的，比如 6 3 /,先弹出3，然后弹出6，所以你要定义好两个变量去保存，别搞乱顺序运算
*/
class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> que = new ArrayDeque<>();
        for (String ch:tokens) {
            if ("+".equals(ch) || "-".equals(ch) || "*".equals(ch)|| "/".equals(ch)){//力扣的问题，不能用==，只能用equals
                int temp1 = que.pop();
                int temp2 = que.pop();
                if ("+".equals(ch)) {
                    que.push(temp2 + temp1);
                } else if ("-".equals(ch))  {
                    que.push(temp2 - temp1);
                } else if ("*".equals(ch))  {
                    que.push(temp2 * temp1);
                } else if ("/".equals(ch))  {
                    que.push(temp2 / temp1);
                } 
            } else {
                    que.push(Integer.valueOf(ch));
            } 
        }
        return que.pop();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/*
就是上面解法的简化版，但是需要注意减法和除法，而上面则不需要顾虑太多
*/
class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> que = new ArrayDeque<>();
        for (String ch:tokens) {
            if ("+".equals(ch)) {
                que.push(que.pop() + que.pop());
            } else if ("-".equals(ch))  {
                que.push(-que.pop() + que.pop());//这里需要前面加个负号
            } else if ("*".equals(ch))  {
                que.push(que.pop() * que.pop());
            } else if ("/".equals(ch))  {//除法要注意
                int temp1 = que.pop();
                int temp2 = que.pop();
                que.push(temp2 / temp1);
            } else {
                que.push(Integer.valueOf(ch));
            }
        }
        return que.pop();

    }
}

239 滑动窗口最大值 hard

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
巩固知识
add/offer/offerLast添加队尾，三个方法等价；
push/offerFirst添加队头，两个方法等价。
remove/pop/poll/pollFirst删除队头，四个方法等价；
pollLast删除队尾。


add/remove源自集合，添加到队尾 / 从队头删除；
offer/poll源自队列 添加到队尾/ 从队头删除；
push/pop源自栈   添加到队头/ 从队头删除；
offerFirst/offerLast/pollFirst/pollLast源自双端队列（两端都可以进也都可以出），offerFirst添加到队头，offerLast添加到队尾，pollFirst从队头删除，pollLast从队尾删除。

peek()方法用于返回此双端队列表示的队列的头元素，但不删除该元素。

java最好别用Stack来实现栈的功能，官方说的，不推荐使用，所以可以用deque来做栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/*
这个题是用单调队列来完成的
队列中只用于保存位置，而不是保存nums的具体值，这样的原因是，可以用于判断是否超过了滑动窗口的范围。
队列的头代表的位置始终是值最大的
具体操作：
首先判断队列中的范围是否超过滑动窗口的范围，如果超过了，则要移除，因为先进入队列的位置是最早的，所以看队列的头来判断
然后判断nums[i]是否比队列尾巴所代表的nums值要大，如果大了，就移除队尾的元素，但是小于可以插进去队列，这也说明队列是单调的，单调递减
最后就是把结果放入res中
*/
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        ArrayDeque<Integer> deque = new ArrayDeque<>();
        int n = nums.length;
        int[] res = new int[n - k + 1];
        int x = 0;
        for (int i = 0; i < n; i++) {
            while (!deque.isEmpty() && deque.peek() < i - k + 1) {//判断队头是否超过滑动窗口的范围
                deque.poll();
            }
            while(!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {//保证单调，判断队尾是否小于下一个值，如果是，就不断移除队列尾元素，直到符合要求
                deque.pollLast();
            }
            deque.offer(i);
            if (i >= k - 1) {//比如k=3，i从2开始就可以取出元素放了，然后每移动一次都放一次
                res[x++] = nums[deque.peek()];
            }
        }
        return res;
    }
}

347 前k个高频元素 medium

之前做过，但是发现之前的方法有点复杂，下面是小顶堆的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        int[] result = new int[k];
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        Set<Map.Entry<Integer, Integer>> entries = map.entrySet();

        PriorityQueue<Map.Entry<Integer, Integer>> queue = new PriorityQueue<>((o1, o2) -> o1.getValue() - o2.getValue());
        for (Map.Entry<Integer, Integer> entry : entries) {
            queue.offer(entry);
            if (queue.size() > k) {
                queue.poll();
            }
        }
        for (int i = 0; i < k; i++) {
            result[i] = queue.poll().getKey();
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
思路是首先是先用map来存储key和value，value就是统计次数。
set来保存这个键值后构建小顶堆，小顶堆poll掉的是小数，留下来的是大数，然后判断队列中的大数是否超过k
超过k就poll掉，最后用一个数组来保留结果。


下面是一些语法记录：以[1,1,1,2,2,3], k = 2为例子
map不能直接使用迭代器，所以用set
map有一个方法叫做entrySet(),这方法可以将Map的键值对的映射关系作为set集合的元素存储到Set集合当中，而这种映射关系的类型就是Entry的类型。
Map.Entry是Map声明的一个内部接口，此接口为泛型，定义为Entry<K,V>。它表示Map中的一个实体（一个key-value对）。接口中有getKey(),getValue方法。
Set<Map.Entry<Integer, Integer>> entries = map.entrySet();
上面这句话打印出来的entries是[1=3, 2=2, 3=1]
当然了，直接打印map.entrySet()打印出来也是[1=3, 2=2, 3=1]，用set还是为了能够迭代


构建小顶堆的作用是能保证每次取出的元素都是队列中权值最小的
如果是大顶堆则是new PriorityQueue<>((o1, o2) -> o2.getValue() - o1.getValue());
PriorityQueue（优先队列）


add和remove是一对，源自Collection；
offer和poll是一对，源自Queue；
push和pop是一对，源自Deque，其本质是栈（Stack类由于某些历史原因，官方已不建议使用，使用Deque代替）；
offerFirst/offerLast和pollFirst/pollLast是一对，源自Deque，其本质是双端队列。

二叉树

递归三部曲：
1.确定递归函数的参数和返回值
2.确定终止条件
3.确定单层递归的逻辑

务必熟悉定义二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {};//{}容易漏
    TreeNode(int val) {
        this.val = val;
    }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}
/*
这里注意下递归中reurn的问题
如果是TreeNode 一般return null;
如果是获得元素的值，这里的return代表终止运行程序，也不能return 0哦，直接终止即可，看530。
如果求深度，就return 0 看104
如果判断是话 就return true 看98
*/

94/144/145 二叉数递归遍历（递归法） easy

递归遍历三步骤：1.确定输入的参数和返回值（定义递归函数入口） 2.确定终止条件 3.确定递归逻辑（函数内容）

144 前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        preOrder(root, result);
        return result;
    }
    public void preOrder(TreeNode root, List<Integer> result) {
        if (root == null) return;

        result.add(root.val);
        preOrder(root.left, result);
        preOrder(root.right, result);
    }
}

94 中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result =  new ArrayList<Integer>();
        inOrder(root, result);
        return result;
    }
    public void inOrder(TreeNode root, List<Integer> result) {
        if (root == null) return;
        inOrder(root.left, result);
        result.add(root.val);
        inOrder(root.right, result);
    }
}

145 后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result =  new ArrayList<Integer>();
        postOrder(root, result);
        return result;
    }
    public void postOrder(TreeNode root, List<Integer> result) {
        if (root == null) return;
        
        postOrder(root.left, result);
        postOrder(root.right, result);
        result.add(root.val);
    }
}

94/144/145 二叉数递归遍历（迭代法） easy

144 前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/*
前序遍历是中-左-右，迭代法用栈来解决 入栈的顺序是中-右-左
需要注意的是，栈是先进后出，所以如果要达到中左右的效果，需要右边先进栈，这样就可以后出。
还需要注意stack的类型是TreeNode哦
*/
class Solution {
    
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();//去掉ArrayList<Integer>中的Integer也可以的
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()) {
            TreeNode node =  stack.pop();
             result.add(node.val);
            if (node.right != null) {
                stack.push(node.right);
            }
            if (node.left != null) {//这里务必注意不能写成else if，比如[3,1,2]，如果这样写答案为[3,2],因为if else只会判断一次，这样就把left给丢掉了
                stack.push(node.left);
            } 
        }
        return result;
    }
}

94 中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/*
中序遍历：左-中-右
迭代法就是先把左节点全部压进栈中，然后等空了就弹出来顺便取值，然后再压右节点进去
*/
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        while (!stack.isEmpty() || root != null) {
            if (root != null) {
                stack.push(root);
                root = root.left;
            } else {
                root = stack.pop();
                result.add(root.val);
                root = root.right;
            }
        }
        return result;
    }
}

145 后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/*
后序遍历顺序 左-右-中 入栈顺序：中-左-右 出栈顺序：中-右-左， 最后翻转结果。
和前序迭代法很相似，只有两个地方不同：1.压栈顺序2.结果翻转
*/
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();//去掉ArrayList<Integer>中的Integer也可以的
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()) {
            TreeNode node =  stack.pop();
             result.add(node.val);
            if (node.left != null) {
                stack.push(node.left);//先压左边
            }
            if (node.right != null) {
                stack.push(node.right);
            } 
        }
        Collections.reverse(result);//最后要翻转
        return result;
    }
}

94/144/145 二叉数递归遍历（统一迭代法） easy

因为迭代法的写法是针对每种遍历顺序定制的，没有统一的规律，所以才有统一迭代法。
144 前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/*
前序遍历：中-左-右   在本方法的压栈顺序为：右-左-中
中序遍历：左-中-右   在本方法的压栈顺序为：右-中-左 
后序遍历：左-右-中   在本方法的压栈顺序为：中-右-左


这里有个细节的地方就是添加了中节点后还添加了一个null节点，那么读取的时候，会不会读到null呢
答案是会的，但是当我们读到null时候（每次while都会重新读取栈顶），就会触发else这里，然后继续pop取值，这时候就是一个新的node，然后加入该节点的val进入结果中 

push和pop是一对

第二次做的反思，首先没有考虑到倒着顺序进行进栈和压栈
其次，在内部node的处理上，还是还是习惯写成root，感觉自己就像背题一样而没有去理解题目
*/
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);//压入root
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();//提取栈顶元素并删除
            if (node != null) {
                if (node.right != null) stack.push(node.right);//添加右节点（空节点不入栈）
                if (node.left != null) stack.push(node.left);//添加左节点（空节点不入栈）
                stack.push(node);// 添加中节点
                stack.push(null);// 中节点访问过，但是还没有处理，加入空节点做为标记。                
            } else {//只有遇到空节点的时候，才将下一个节点放进结果集
                node = stack.pop();
                result.add(node.val);
            }
        }
        return result;
    }
}

因为不推荐用stack，这里用LinkedList替代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/*
LinkedList中的pop()和poll()的区别
poll是队列数据结构实现类的方法，从队首获取元素，同时获取的这个元素将从原队列删除
pop是栈结构的实现类的方法，表示返回栈顶的元素，同时该元素从栈中删除，当栈中没有元素时，调用该方法会发生异常

同样，还有push，offer和add区别
push是把LinkedList当做栈来用
offer和add是当做链表或者队列来用
*/
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        if (root == null) return result;
        LinkedList<TreeNode> stack = new LinkedList<>();//List是没有push方法的，所以前面是LinkedList<TreeNode>
        stack.push(root);
        while(!stack.isEmpty()) {
            TreeNode temp = stack.pop();
            if (temp != null) {
                if (temp.right != null) stack.push(temp.right);
                if (temp.left != null) stack.push(temp.left);
                stack.push(temp);
                stack.push(null);
            } else {
                temp = stack.pop();
                result.add(temp.val);
            }
        }
        return result;
    }
}

94 中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                if (node.right != null) stack.push(node.right);
                stack.push(node);
                stack.push(null);  
                if (node.left != null) stack.push(node.left);              
            } else {
                node = stack.pop();
                result.add(node.val);
            }
        }
        return result;
    }
}

145 后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                stack.push(node);
                stack.push(null); 
                if (node.right != null) stack.push(node.right);    
                if (node.left != null) stack.push(node.left);           
            } else {
                node = stack.pop();
                result.add(node.val);
            }
        }
        return result;
    }
}

102 二叉树的层序遍历 medium

用队列先进先出的特性，对每层保存然后poll出来，顺序就是层序遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/*
具体解法：
对每一层进行操作，那么怎么判断是这层呢
用len来判断，当队列加完这层后，再用len计算长度，然后一个个出列，处理完一层，再处理一层，这样就做到层序遍历。
*/
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<List<Integer>>();//注意我们输出的格式如[[[1],[2,3],[4,5,6]]]
        if (root == null) return result;
        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();//队列存的是TreeNode
        queue.offer(root);
        while (!queue.isEmpty()) {
            List<Integer> ietmList = new ArrayList<Integer>();//先定义
            int len = queue.size();//记录长度
            while (len-- > 0) {//while哦，一直加节点
                TreeNode temp = queue.poll();//第二次做的时候，把这个放到了while上面，不应该！
                ietmList.add(temp.val);
                if (temp.left != null) queue.offer(temp.left);//这里是temp不是root
                if (temp.right != null) queue.offer(temp.right);
            }
            result.add(ietmList);
        }
        return result;
    }
}

226 翻转二叉树 easy

递归法，可以对比下前序遍历的递归（后序也可以，但是不可以用中序）。
做这个题一开始用List去保存，哎，年轻。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return null;//root也可以
        swapTree(root);
        invertTree(root.left);
        invertTree(root.right);//第二次写，居然写成swapTree，实质上还是没有理解好递归,处理根的时候，就是交换，然后左右就是递归
        return root;

    }
    public void swapTree(TreeNode node) {//第二次写的时候写了TreeNode left，TreeNode right两个参数，其实不需要，按照遍历递归，先处理左边，再处理右边
        TreeNode temp = node.left;
        node.left = node.right;
        node.right = temp;
    }
}

层序遍历，可以好好看看

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return null;
        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int len = queue.size();
            while (len-- > 0) {
                TreeNode temp = queue.poll();
                swapTree(temp);
                if (temp.left != null) queue.offer(temp.left);
                if (temp.right != null) queue.offer(temp.right);
            }
        }
        return root;
    }
    public void swapTree(TreeNode node) {
        TreeNode temp = node.left;
        node.left = node.right;
        node.right = temp;
    }
}

101 对称二叉树 easy

判断是不是对称二叉树，返回true或者false，用了递归法内外是否一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/*
对称，那么就是判断内外是否一样

先判断节点空的三种情况：都空，左空，右空。
然后都不空了，判断值是否相等，但是这里只能判断不等的情况返回false，不能写成相等情况返回true，理由如下：
此时就是：左右节点都不为空，且数值相同的情况，已经被我们过滤完了，此时才做递归，做下一层的判断

所以如果你是判断了相同的，但是可能不同的没有过滤就进入递归了

再一次做还是错误，首先是大概有印象是用内外，但是没有用到函数compare，导致一直写错
*/
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return compare(root.left, root.right);
    }
    public boolean compare(TreeNode left, TreeNode right) {
        if (left == null && right == null) return true;
        if (left == null && right != null) return false;
        if (left != null && right == null) return false;
        if (left.val != right.val) return false;//注意不能写成if (left.val == right.val) return true; 
        boolean outSide = compare(left.left, right.right);
        boolean inSide = compare(left.right, right.left);
        return outSide && inSide;
    }
}

104 二叉树最大深度 easy

使用递归法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/*
1.确定参数
2.确定终止条件
3.递归逻辑：先求它的左子树的深度，再求的右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。
*/
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0; 
        int left = maxDepth(root.left);//左
        int right = maxDepth(root.right);//右
        int depth = 1 + Math.max(left, right);//中
        return depth;
    }
}

111 二叉树的最小深度 easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/*
这个最小深度和最大深度是有区别的
比如，如果左子树都是空的，右子树一直叠加，那么最小深度，是算右子树那边的
那么就需要做出一个判断

第二次做的时候，没有考虑到要同时满足条件再返回1+right或者left
*/
class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) return 0; 
        int left = minDepth(root.left);//左
        int right = minDepth(root.right);//右
        if (root.left == null && root.right != null) {//左边空，右边不空，则返回右边长度，可以直接写成if (root.left == null)
            return 1 + right;
        }
        if (root.left != null && root.right == null) {
            return 1 + left;
        }        
        int depth = 1 + Math.min(left, right);//找到最小值
        return depth;
    }
}

222 完全二叉树的节点个数 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/*
层序遍历即可，这个是自己想到的，然后套用前面的代码修改
*/
class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        Deque<TreeNode> queue = new ArrayDeque<TreeNode>();
        int result = 0;
        queue.offer(root);
        while (!queue.isEmpty()) {
            int len = queue.size();
            while (len-- > 0) {
                result += 1;
                TreeNode temp = queue.poll();
                if (temp.left != null) queue.offer(temp.left);
                if (temp.right != null) queue.offer(temp.right);
            }
        }
        return result;
    }
}

110 平衡二叉树 easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/*
关于深度和高度，这只是力扣中的定义，其他教科书可能不一样
二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

关于这个题，首先要了解平衡二叉树的概念，然后如果已经检测到左右子树相差大于1，剩下都是返回-1，否则返回的是正常高度。

第二次做存在的问题：
1.没有想到用一个辅助getheight函数，注意这个题是返回一个true还是false，而我们当然要用高度来判断
2.遗忘左-右绝对值的问题
3.需要注意如果已经不平衡的情况
*/
class Solution {
    public boolean isBalanced(TreeNode root) {
        return getHeight(root) != -1;//不为-1，就返回true
    }
    public int getHeight(TreeNode root) {
        if (root == null) return 0;
        int left = getHeight(root.left);
        int right = getHeight(root.right);
        if (left == -1) return -1;//如果已经不平衡了，就返回-1
        if (right == -1) return -1;//如果已经不平衡了，就返回-1
        if (Math.abs(left - right) > 1) return -1;//Math.abs函数
        return 1 + Math.max(left, right);
    }
}

257 二叉树的所有路径 easy

代码此链接

1
2
3
4
5
6
以前做过，为什么又忘记，这次复查到的问题：
constructpath(root, "", paths);//中间的参数，不能有空格，
StringBuffer是append，还有需要toString()
ArrayList是add
递归函数里面的if else是套在第一个if中的
递归：1.确定参数2.终止条件3.确定递归逻辑

这个代码主要是为了方便理解回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>();
        if (root == null) return res;
        List<Integer> path = new ArrayList<>();
        preorderdfs(root, res, path);
        return res;
    }
    public void preorderdfs(TreeNode root, List<String> res, List<Integer> path) {
        path.add(root.val);//容易漏
        if (root.left == null && root.right== null) {
            StringBuffer sb = new StringBuffer();
            for (int i = 0; i < path.size() - 1; i++) {
                sb.append(path.get(i)).append("->");//注意这里是先加节点，然后继续加"->"
            }
            sb.append(path.get(path.size() - 1));//因为最后一个的后面不需要加"->"，所以单独拿出来
            res.add(sb.toString());
            return;
        } 
        if (root.left != null) {
            preorderdfs(root.left, res, path);
            path.remove(path.size() - 1);//回溯
        }

        if (root.right != null) {
            preorderdfs(root.right, res, path);
            path.remove(path.size() - 1);//回溯
        }
    }
}

全局变量的写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    List<String> result = new ArrayList<>();//第二次居然写成List<List<String>>
    LinkedList<Integer> path = new LinkedList<>();

    public List<String> binaryTreePaths(TreeNode root) {
        if (root == null) return result;
        backtrack(root);
        return result;
    }
    public void backtrack(TreeNode root) {
        path.add(root.val);//第二次写漏了

        if (root.left == null && root.right == null) {
            StringBuilder sb = new StringBuilder();
            for (int i = 0; i < path.size() - 1; i++) {
                sb.append(path.get(i)).append("->");//不要写成sb.append(path.get(i).append("->"));append要放在外面
            }
            sb.append(path.get(path.size() - 1));
            result.add(sb.toString());
            return;
        }
        if (root.left != null) {
            backtrack(root.left);
            path.remove(path.size() - 1);
        }
        if (root.right != null) {
            backtrack(root.right);
            path.remove(path.size() - 1);
        }
    }
}

404 左叶子之和 easy

有点像求深度那个题，也是左右中的顺序，不同点是判断左叶子节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) return 0;

        int left = sumOfLeftLeaves(root.left);//左子树的情况
        int right = sumOfLeftLeaves(root.right);//右子树的情况
        int mid = 0;
        if (root.left != null && root.left.left == null && root.left.right == null) {
            mid = root.left.val;
        }
        int sum = left + right + mid;
        return sum;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/*
迭代法，这个和层序遍历还是有一点点差别的，没有len之后进行循环，这个要注意
*/
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        LinkedList<TreeNode> queue = new LinkedList<>();
        if (root == null) return 0;
        int sum = 0;
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if (node.left != null && node.left.left == null && node.left.right == null) {
                sum += node.left.val;               
            }
            if (node.left != null) queue.offer(node.left);
            if (node.right != null) queue.offer(node.right);            
        }
        return sum;
    }
}

513 找树左下角的值 medium

用层序遍历的思路即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/*
这个代码是根据层序遍历后自己写的，但是写的不好，可以看第二个代码
*/
class Solution {
    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);
        int result = 0;
        int flag = 0;
        while (!queue.isEmpty()) {
            int len = queue.size();
            while (len > 0) {
                TreeNode temp = queue.poll();
                if (flag == 0) result = temp.val;
                if (temp.left != null) queue.offer(temp.left);
                if (temp.right != null) queue.offer(temp.right);
                len--;
                if (len == 0) {//我这里设置了一个标志，当len为0，代表循环准备进入下一层
                    flag = 0;
                } else {
                    flag = 1;
                }
            }
        }
        return result;
    }
}

迭代法一直没调试好while，就是类似于层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);
        int result = 0;
        while (!queue.isEmpty()) {
            int len = queue.size();//需要注意的是，len不用再--
            for (int i = 0; i < len; i++) {//这里用for就会简洁很多
                TreeNode temp = queue.poll();
                if (i == 0) result = temp.val;
                if (temp.left != null) queue.offer(temp.left);
                if (temp.right != null) queue.offer(temp.right);
            }
        }   
        return result;
    }
}

路径总和

112 路径总和 easy

这个题目表达的不太清楚，实际上是判断路径有没有符合targetsum，只要有一个符合就返回true。

1
2
3
4
5
6
7
8
9
10
11
12
/*
用减法来一步步走，走到最后叶子节点，如果此时target和叶节点相等，就说明找到了，这个题目只需要找到一个即可。
*/
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) return false;

        if (root.left == null && root.right == null) return targetSum == root.val;

        return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
    }
}

113 路径总和2 easy

这个题要结合257，还有就是257的返回值和这个题不一样，257需要箭头指向，也就是类型是String，具体看是如何处理的，和112的区别是需要把target值都符合的添加进来，这三个题都要好好敲一遍。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;
        List<Integer> path = new ArrayList<>();
        preorderdfs(root, targetSum, res, path);
        return res;
    
    }
    public void preorderdfs(TreeNode root, int targetSum, List<List<Integer>> res, List<Integer> path) {
        path.add(root.val);
        if (root.left == null && root.right == null) {
            if (targetSum == root.val) {
                res.add(new ArrayList<>(path));
            }
            return;
        }

        if (root.left != null) {
            preorderdfs(root.left, targetSum - root.val, res, path);
            path.remove(path.size() - 1);//回溯
        }
        if (root.right != null) {
            preorderdfs(root.right, targetSum - root.val, res, path);
            path.remove(path.size() - 1);//回溯
        }
    }
}

通过中序和前序/后序构建二叉树

1
2
3
4
5
6
7
8
9
10
首先要务必清楚要有中序遍历，前序和后序是不能组成二叉树的。
这里只讲后序和中序构造二叉树。
后序是：左右根
中序是：左根右
所以我们先从后序的最后一个数字可以定位根节点，然后在中序中找到这个值，就可以区分左子树和右子树啦
也就是定义一个helper，这是用中序来构建二叉树。

以后序遍历为例子的思路：
首先把中序的值按照<值，序号>来存到map中，因为后面我们要用后序数组的值来寻找中序数组的序号，所以用<值>可以找到中序的<下标序号>
然后在主方法中，先找到后序根的值，然后用map来定位到中序的index，然后新建root即可，注意后序的话要先构建右子树，再构建左子树

105 从前序与中序遍历序列构造二叉树 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    int[] preorder;
    int[] inorder;
    int pre_idx;
    Map<Integer, Integer> map = new HashMap<Integer, Integer>();
    public TreeNode helper(int left, int right) {
        if (left > right) {
            return null;
        }
        int rootval = preorder[pre_idx];
        TreeNode root = new TreeNode(rootval);
        pre_idx++;
        int index = map.get(rootval);
        root.left = helper(left, index - 1);
        root.right = helper(index + 1, right);
        return root;

    }
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        this.inorder = inorder;
        int pre_idx = 0;
        int idx = 0;
        for (Integer val : inorder) {
            map.put(val, idx++);
        }
        return helper(0, preorder.length - 1);

    }
}

106 从中序与后序遍历序列构造二叉树 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    int[] inorder;//成员变量
    int[] postorder;
    int post_idx;
    Map<Integer, Integer> map = new HashMap<Integer, Integer>();
    public TreeNode helper(int left, int right) {
        if (left > right) {
            return null;
        }
        int rootval = postorder[post_idx];
        post_idx--;
        TreeNode root = new TreeNode(rootval);
        int index = map.get(rootval);
        root.right = helper(index + 1, right);//注意这里有需要先创建右子树，再创建左子树的依赖关系。可以理解为在后序遍历的数组中整个数组是先存储左子树的节点，再存储右子树的节点，最后存储根节点，如果按每次选择「后序遍历的最后一个节点」为根节点，则先被构造出来的应该为右子树。
        root.left = helper(left, index - 1);
        return root;
    }
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        this.inorder = inorder;//使用this关键字指成员变量的值
        this.postorder = postorder;
        post_idx = postorder.length - 1;
        int idx = 0;
        for (Integer val : inorder) {
            map.put(val, idx++);
        }
        return helper(0, inorder.length - 1);
    }
}

654 最大二叉树 medium

首先就是找到最大的值的下标，然后切成左边和右边，用前序遍历递归构造。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/*
左闭右闭区间，和上面的106题目一样
*/
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return construct(nums, 0, nums.length - 1);
    }
    public TreeNode construct(int[] nums, int l, int r) {
        if (l > r) return null;//这里是大于
        int max_i = max(nums, l ,r);//每次递归都要重新找最大值的下标
        TreeNode root = new TreeNode(nums[max_i]);//前序构造二叉树
        root.left = construct(nums, l , max_i - 1);//这里是-1
        root.right = construct(nums, max_i + 1, r);
        return root;
    }
    public int max(int[] nums, int l, int r) {
        int max_i = l;
        for (int i = l; i <= r; i++) {//这里是小于等于
            if (nums[max_i] < nums[i]) {
                max_i = i; 
            }
        }
        return max_i;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/*
左闭右开区间，这里我觉得不如左闭右开区间好记
*/
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return construct(nums, 0, nums.length);
    }
    public TreeNode construct(int[] nums, int l, int r) {
        if (l == r) return null;
        int max_i = max(nums, l ,r);//每次递归都要重新找最大值的下标
        TreeNode root = new TreeNode(nums[max_i]);//前序构造二叉树
        root.left = construct(nums, l , max_i);//注意这里还是max_i
        root.right = construct(nums, max_i + 1, r);
        return root;
    }
    public int max(int[] nums, int l, int r) {
        int max_i = l;
        for (int i = l; i < r; i++) {
            if (nums[max_i] < nums[i]) {
                max_i = i; 
            }
        }
        return max_i;
    }
}

617 合并二叉树 easy

总体比较简单，看递归的返回值处理，其实就是两个二叉树覆盖在一起,思路就是重新构造一个二叉树。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) return root2;//root1空就返回root2
        if (root2 == null) return root1;

        int val = root1.val + root2.val;
        TreeNode root = new TreeNode(val);
        root.left = mergeTrees(root1.left, root2.left);
        root.right = mergeTrees(root1.right, root2.right);
        return root;
    }
}

700 二叉搜索树的搜索 easy

需要注意的是，在递归的时候是用return，另外要了解搜索树的构造。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/*
也可以写成
        if (root == null) return null;
        if (root.val == val) return root;
这里是思路就是根据二叉搜索树的特点，找到了就返回root，如果大于就递归左子树，小于就递归右子树

*/
class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) return root;

        return searchBST(root.val > val ? root.left: root.right, val);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
/*
这个感觉代码上不够简洁
*/
class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) return root;
        
        if (root.val < val) return searchBST(root.right, val);//这里是用return，当前节点小，就要去右子树查找
        if (root.val > val) return searchBST(root.left, val);

        return null;//最后是返回null
    }
}

98 验证二叉搜索树 medium

第二次做又忘记，二叉搜索树中序遍历是升序的，根据这个特性来完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    long pre = Long.MIN_VALUE;//重要！注意前面声明是long而不是Long
    public boolean isValidBST(TreeNode root) {
        if (root == null) return true;
        if (!isValidBST(root.left)) {//如果左边有false，就返回false
            return false;
        }
        if (root.val <= pre) {//不符合二叉搜索树的定义
            return false;
        }
        pre = root.val;//记录上一个遍历的节点
        return isValidBST(root.right);
    }
}

下面这个代码只是为了说明pre的位置也很重要，这个代码更好理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    long pre = Long.MIN_VALUE;//重要！注意前面声明是long而不是Long
    public boolean isValidBST(TreeNode root) {
        if (root == null) return true;
        boolean l = isValidBST(root.left);

       //如果pre = root.val写在这里，又会覆盖掉，导致无法判断下面
        if (root.val <= pre) {//关键部分，如果根比左边小，就肯定不符合了
            return false;
        }

        pre = root.val;//记录上一个遍历的节点
        boolean r = isValidBST(root.right);
        //如果放到这里是出错的 pre = root.val;
        return l && r;//左右都是true才能返回true
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
下面重点来解释
首先利用二叉搜索树升序的特性来做，也就是左子树<根<右子树
所以递归顺序是左根右

先说第一个long pre = Long.MIN_VALUE;
为什么不用int，因为测试案例的原因，不解释了
这里主要解释为什么要用min，因为后台测试数据中有int最小值，也就是有极端情况
有这个案例：[-2147483648]这个是int的最小值，如果你的pre随便设置，最后结果是false，但是其实这个也算二叉搜索树，因为递归过程中会比较pre和root.val，你的pre这时候是大于val的，所以会false


第二个重点解释 pre = root.val;的位置问题，如果根据第二个解答写在r的下面
对于[5,1,4,null,null,3,6]案例是错误的答案，输出是true，但是实际上是false
画出这个二叉树，可以发现右子树中是出现一个3，二叉搜索树的定义是根要比所有的右子树都小，你现在根比右边大，就是不合理的。
所以进入右边之前，要保存上一个root的val，但是其实我觉得还有一个理解就是递归顺序就是左-根-右，这个pre其实就是递归到根的情况
这样才可以用中序遍历 左边小于右边来比较

530 二叉搜索树的最小绝对差 medium

根据二叉搜索树的定义，用中序遍历完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/*
这个自己写的，可能有些不够简练,但是好记

*/
class Solution {
    public int getMinimumDifference(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        traversal(root, result);
        int res = Integer.MAX_VALUE;
        for (int i = 0; i < result.size() - 1; i++) {
            res = Math.min(res, result.get(i + 1) - result.get(i));
        }
        return res;
    }
    public void traversal(TreeNode root, List<Integer> result) {
        if (root == null) return;
        traversal(root.left, result);
        result.add(root.val);
        traversal(root.right, result);
    }
}

下面这个代码更精简

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    TreeNode pre;
    int result = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        if (root == null) return 0;
        traversal(root);
        return result;
    }
    public void traversal(TreeNode root) {//使用中序遍历，和上一个题类似哦
        if (root == null) return;
        traversal(root.left);
        if(pre != null) {
            result = Math.min(result, root.val - pre.val);
        }
        pre = root;//记录上一个节点
        traversal(root.right);
    }
}

501 二叉搜索树的众数 easy

用了中序遍历，也是利用二叉搜索树的性质，中序遍历是按照顺序升序的，主要是理解处理的逻辑。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/*
和98题结合看，一样是用中序的逻辑和pre，但是这里的pre初始化是null，和98的不一样
*/
class Solution {
    TreeNode pre = null;
    ArrayList<Integer> list = new ArrayList<>();
    int count = 0;
    int maxcount = 0;
    public int[] findMode(TreeNode root) {
        traversal(root);
        int result[] = new int[list.size()];
        for (int i = 0; i < list.size(); i++) {
            result[i] = list.get(i);
        }
        return result;

    }
    public void traversal(TreeNode root) {
        if (root == null) return;
//左
        traversal(root.left);
//根
        if (pre != null && pre.val != root.val) {
            count = 1;
        } else {
            count++;
        }
        if (count > maxcount) {
            list.clear();//删除动态数组中的所有元素
            list.add(root.val);//第二次写的时候忘记这里的逻辑
            maxcount = count;
        } else if (count == maxcount){
            list.add(root.val);
        }
        pre = root;

//右
        traversal(root.right);
    }
}

236 二叉树的最近公共祖先 medium

这个题需要好好看卡哥的讲解。这里容易漏掉一种情况，就是p是q的祖先，或者反过来，第二次看这个题还是没有想到为什么用后序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/*
需要从小到上，也就是先获取叶子节点，所以后序遍历
用递归的解法
*/
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) {//第二次写居然写成p == null，q == null，还是理解不到位，这里要理解为如果找到了 节点p或者q，或者遇到空节点，就返回。
            return root;//注意不是返回null
        }
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if (left == null && right == null) {// 若未找到节点 p 或 q
            return null;
        } else if (left != null && right == null) {// 若找到一个节点
            return left;
        } else if (left == null && right != null) {// 若找到一个节点
            return right;
        } else {// 若找到两个节点
            return root;
        }
    }
}

235 二叉搜索树的最近公共祖先 easy

用上面一个代码也是可以的，不过我们可以利用二叉搜索树的性质来完成。也就是如果root的值都小于p和q，那就去右区间找，如果都大于就在左区间找，如果在p和q的区间内，说明找到，就返回root。

1
2
3
4
5
6
7
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
        else if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
        else return root;
    }
}

701 二叉搜索树中的插入操作 medium

利用二叉搜索树的性质来插入。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {//找到插入节点的位置了，并把插入的节点返回
            return new TreeNode(val);//第二次做手误写成root.val
            /*或者写成这样
            TreeNode node = new TreeNode(val);
            return node;
            */    
        }
        //通过递归函数返回值完成了新加入节点的父子关系赋值操作了，下一层将加入节点返回，本层用root->left或者root->right将其接住
        if (root.val < val) {
            root.right = insertIntoBST(root.right, val);// 第二次做居然写成return了
        } else if (root.val > val) {
            root.left = insertIntoBST(root.left, val);
        }
        return root;//一直容易忘记这个
    }
}

450 删除二叉搜索树中的节点 medium

有点难度的题，下面有具体解释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;//情况1

        if (root.val > key) {
            root.left = deleteNode(root.left, key);
        } else if (root.val < key) {
            root.right = deleteNode(root.right, key);
        } else if (root.val == key) {
            if (root.left == null && root.right == null) return null;//情况2
            if (root.right == null) return root.left;//情况3
            if (root.left == null) return root.right;//情况4
            TreeNode temp = root.right;//情况5
            while (temp.left != null) {
                temp = temp.left;
            }
            root.val = temp.val;
            root.right = deleteNode(root.right, temp.val);//因为这个节点是root的右孩子中，所以用root的右孩子作为新root，同时删除这个节点原来的位置。
        }
        return root;//最后别忘了返回root
    }
}
1
2
3
4
5
6
7
8
9
一共五种情况
1.没找到删除的节点，直接返回null
然后开始搜索正确的位置，找到节点的情况
2.左右孩子都是空的，返回null
3.右孩子空，把左孩子补上去
4.左孩子空，把有孩子补上去
5.有左右孩子，这个情况最复杂，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点，下面详细讲操作。

先找到这个key的右孩子，然后一直找这个右孩子的最左边的孩子，这时候就顺便把这个孩子的节点值设为root，然后递归删除这个值。

669 修剪二叉搜索树 medium

把范围之外的节点清除。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
/*
在边界范围外的，好好看看下面的注释，为什么要return,和上一题对比

*/    
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) return null;//第二次做的时候漏了，任何情况都要考虑空

        if (root.val < low) {//不在范围内的节点，需要继续寻找。小于val，就去右边区间寻找，抛弃其左子树整体。
            return trimBST(root.right, low, high);// 如果当前结点小于下界，直接将修剪后的右子树替换当前节点并返回，所以要return
        }
        if (root.val > high) {//不在范围内的节点，需要继续寻找。大于val，就去左边区间寻找，抛弃其右子树整体。
            return trimBST(root.left, low, high); // 如果当前结点大于上界，直接将修剪后的左子树替换当前节点并返回
        }
        //如果数字在区间内,就去裁剪左右子节点
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}

108 将有序数组转换为二叉搜索树 easy

可以对比下构造二叉树那个题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return bst(nums, 0, nums.length - 1);//因为下面的递归是用左闭右闭区间，所以长度-1。

    }
    public TreeNode bst(int[] nums, int left, int right) {
        if (left > right) return null;//左闭右闭的区间，所以当区间 left > right的时候，就是空节点了
        int mid = left + (right - left) / 2;
        TreeNode root = new TreeNode(nums[mid]);//构造中间节点
        //然后构造两边
        root.left = bst(nums, left, mid - 1);//mid已经用了，所以要减1
        root.right = bst(nums, mid + 1, right);
        return root;
    }
}

538 把二叉搜索树转换为累加树 medium

这个先看定义，就是使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。中序遍历是升序，这样不方便累加，要从后往前，也就是中反的中序遍历，右中左。

1
2
3
4
5
6
7
8
9
10
class Solution {
    int sum = 0;//定义sum
    public TreeNode convertBST(TreeNode root) {
        if (root == null) return null;
        convertBST(root.right);
        sum += root.val;
        root.val = sum;//这个很关键
        convertBST(root.left);
        return root;
    }

回溯算法

一般用于组合，切割，子集，排列，棋盘问题。
回溯三部曲
1.回溯函数模板返回值以及参数，返回值一般为void
2.回溯终止条件
3.回溯遍历过程
回溯模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {//for可以理解为横向遍历
        处理节点;
        backtracking(路径，选择列表); // 递归，递归可以理解为纵向遍历
        回溯，撤销处理结果
    }
}

关于剪枝操作，这是卡哥原话
剪枝精髓是：for循环在寻找起点的时候要有一个范围，如果这个起点到集合终止之间的元素已经不够 题目要求的k个元素了，就没有必要搜索了。

77 组合 medium

注意取过的数字不再取，也就是没有(4,4)这种情况，组合是无序(也就是(1,2)和(2,1)是一样的，取一个就可以)，排列是有序(两个答案都要)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/*
这个代码没有进行剪枝处理
返回范围 [1, n] 中所有可能的 k 个数的组合
*/
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtrack(n, k ,1);
        return result;

    }
    public void backtrack(int n, int k, int startindex) {
        if (path.size() == k) {
            result.add(new ArrayList<>(path));
            return;//return语句后不带返回值，作用是退出该程序的运行，终止本层的递归
        }
        for (int i = startindex; i <= n; i++) {//startindex是为了让程序知道从哪个数字开始取，不能重复的，for (int i = startindex; i <= n - (k - path.size()) + 1; i++)这是剪枝处理
            path.add(i);//把这个数字加进去
            backtrack(n, k, i + 1);//递归开始，纵向遍历
            path.removeLast();//把这个数字取出来，再加其他数字，比如原来[1,2]，然后把2取出来，把3加进去，就有[1,3]
        }
    }
}
1
2
3
4
LinkedList<Integer> path = new LinkedList<>();
注意这个才有removeLast的操作，arraylist是没有的。
对剪枝的理解
比如 n = 7, k = 4，那么从 5 开始搜索就已经没有意义了，这是因为即使把 5 选上，后面的数只有 6 和 7，一共就 3 个候选数，凑不出 4 个数的组合。因此，搜索起点有上界。

216 组合总和 III medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/*
找出所有相加之和为 n 的 k 个数的组合，只使用数字1到9，每个数字 最多使用一次 
和上一题的区别是，这个题的n的目标数，潜在的范围其实是[1,9]
*/
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backtrack(k, n, 0, 1);
        return result;
    }
    public void backtrack(int k, int n, int sum, int startindex) {
        // 减枝，这句话没有也是可以通过的
        if (sum > n) {
            return;
        }

        if (path.size() == k) {
            if (n == sum) {
                result.add(new ArrayList<>(path));
            }
            return;
        }
        for (int i = startindex; i <= 9; i++){
            path.add(i);
            backtrack(k, n, sum + i, i + 1);//和下面解法的区别
            path.removeLast();
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backtrack(k, n, 0, 1);
        return result;
    }
    public void backtrack(int k, int n, int sum, int startindex) {
        // 减枝，这句话没有也是可以通过的
        if (sum > n) {
            return;
        }

        if (path.size() == k) {
            if (n == sum) {
                result.add(new ArrayList<>(path));
            }
            return;
        }
        for (int i = startindex; i <= 9; i++){//这里也可以进行剪枝
            path.add(i);
            sum += i;//最开始是看到这个写法，后面看到更简洁，就更新了，我觉得和上一个解法的区别是在递归的时候sum有i去控制大小，而这里没有，所以递归后还要减掉。
            backtrack(k, n, sum, i + 1);
            path.removeLast();
            sum -= i;//这里是容易忘记的，因为你回溯，务必减去上一个数
        }
    }
}

17 电话号码的字母组合 medium

这个题和上一题的区别是，这个题相当于多个区间进行取值，而上个题是一个区间内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    List<String> result = new ArrayList<>();
    public List<String> letterCombinations(String digits) {
        if (digits == null || digits.length() == 0) {
            return result;
        }
        String[] numString = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};//这是为了对应2~9，特意空出两个字符
        backtrack(numString, digits, 0);//这个0，是获取第一个digits的数字用的
        return result;
    }
    StringBuilder temp = new StringBuilder();
    public void backtrack(String[] numString, String digits, int num) {
        if (num == digits.length()) {//这个条件也是不一样的，因为在循环数字
            result.add(temp.toString());
            return;
        }
        String str = numString[digits.charAt(num) - '0'];//先把这个数字对应的字母取出来
        for (int i = 0; i < str.length(); i++) {//这就是和上题的区别，i=0，是这个区间的开始，而上一个题的同一个区间，所以要找下一个数
            temp.append(str.charAt(i));//这里是append
            backtrack(numString, digits, num + 1);
            temp.deleteCharAt(temp.length() - 1);//还有这个用法
        }
    }
}

39 组合总和 medium

结合216来看，和216的区别是，这里给了一个数组的范围，其次，数组元素的可以重复使用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>(); 
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);//排序很重要
        backtrack(candidates, target, 0, 0);
        return result;
    }
    public void backtrack(int[] candidates, int target, int sum, int idx) {
        if (sum == target) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = idx; i < candidates.length; i++) {
            if (sum + candidates[i] > target) break;//没有这句也是报错的，如果 sum + candidates[i] > target 就终止遍历
            path.add(candidates[i]);
            backtrack(candidates, target, sum + candidates[i], i);//这里不是i + 1，就体现了可以重复使用这个数组的思想
            path.removeLast(); 
        }
    }
}

40 组合总和 II medium

这里实际上要完成两个任务，一个是不能有重复元素(是指这个数组中不能重复用这个数，但是数组本身是可以有重复是数字的，比如这个数组可以存在两个1，但是每个1只能用一次)，第二个是不能有重复组合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/*
解决不能有重复组合，需要在for中进行去除，也就是对每层的处理
解决不能重复数字以前则遇到过，在回溯的时候，i＋1即可。
*/
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        backtrack(candidates, target, 0, 0);
        return result;

    }
    public void backtrack(int[] candidates, int target, int sum, int idx) {
        if (sum == target) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = idx; i < candidates.length; i++) {
            if (i > idx && candidates[i - 1] == candidates[i]) {
                continue;
            }//这里就是重复组合的问题
            if (sum + candidates[i] > target) break;
            path.add(candidates[i]);
            backtrack(candidates, target, sum + candidates[i], i + 1);//i+1解决重复元素的问题
            path.removeLast();
        }
    }
}

131 分割回文串 medium

回文串 是正着读和反着读都一样的字符串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    LinkedList<String> path = new LinkedList<>();
    List<List<String>> result = new ArrayList<>();

    public List<List<String>> partition(String s) {
        backtrack(s,0);
        return result;
    }
    public void backtrack(String s, int startindex) {
        if (startindex == s.length()) {//切割线到了最后作为终止条件
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = startindex; i < s.length(); i++) {
            if (ishuiwen(s, startindex, i)) {//这里已经判断了是否回文，所以在上面终止条件直接添加结果即可
                String str = s.substring(startindex, i + 1);
                path.add(str);
            } else {
                continue;
            }
            backtrack(s, i + 1);//因为也是不能往回走，所以+1
            path.removeLast();
        }
        
    }
    public boolean ishuiwen(String s, int startindex, int end) {
        for (int i = startindex, j = end; i < j; i++, j--) {
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
首先我们要明白startindex的作用就是相当于切割线的作用
这个题的for循环是切了第一根线（横向），然后回溯递归的过程是纵向（切第二跟线），这样可以实现切割不同字符串的效果。
那么又有一个疑问，为什么是两条线，因为第一条线固定第一个位置，然后第二根线是一个个位置继续切。

问题1：为什么回溯结束条件是if (startindex == s.length())
当切割线到了最后，说明后面不能再切了，所以这里要设置结束条件并添加结果。
可是，这里没有判断回文呀？
其实不是的，下面for循环的时候，已经判断回文，如果不是回文的话，不参加递归，所以，只要参加了递归，就一定是回文。

这个题要好好看卡哥的画图，可以理解这个切割线。

substring(start,end)是左开右闭，也就是end序号是没有截取到了，而我们判断回本的时候，end是参与了判断的，所以这里要加1让这个字符串截取到。

93 复原ip地址 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    List<String> result = new ArrayList<>();
    public List<String> restoreIpAddresses(String s) {
        backtrack(s, 0, 0);
        return result;
    }
    public void backtrack(String s, int startindex, int pointnum) {
        if (pointnum == 3) {
            if (isvalid(s, startindex, s.length() - 1)) {//逗点已经写了3个，也就是切成了4份，最后再判断完第四个区间即可
                result.add(s);
            }
        }
        for (int i = startindex; i < s.length(); i++) {
            if (isvalid(s, startindex, i)) {//substring是左开右闭
                s = s.substring(0, i + 1) + "." + s.substring(i + 1);//在str的后⾯插⼊⼀个逗点
                pointnum++;//记录逗点个数
                backtrack(s, i + 2, pointnum);//插⼊逗点之后下⼀个⼦串的起始位置为i+2
                pointnum--;//回溯的时候恢复
                s = s.substring(0, i + 1) + s.substring(i + 2);//回溯除去逗点
            } else {
                break;//continue也可以
            }
        }
        
    }
    public boolean isvalid(String s, int start, int end) {
        if (start > end) {
            return false;
        }

        if (s.charAt(start) == '0' && start != end) {// start != end是为了这个条件：当[0,0,0,0]，单独传入一个0就是start等于end，所以也可以写成start<end
            return false;
        }
        int num = 0;
        for (int  i = start; i <= end; i++) {//这里的end注意下，是<=哦
            if (s.charAt(i) < '0' || s.charAt(i) > '9') {//这个判断可以省略，案例不存在非法字符
                return false;
            }
            num = num * 10 + (s.charAt(i) - '0');
            if (num > 255) {
                return false;
            }

        }
        return true;//最后返回true也容易忘记
     }
}
1
2
3
4
5
6
7
8
9
这个题和上面题的区别：
1.没有path变量
这个题从头到尾都需要整个s，而之前的题目的类似于从里面选若干个元素。

2.ip有效判断
首先最主要的判断是区间必须是左小右大，也就是start>end是非法的
first：0开头的数字不合法，但是如果单独0的话是可以的，比如[0,0,0,0]
second：遇到⾮数字字符不合法（这个可以不需要，因为案例中都是数字）
third：大于255的不合法

78 子集 medium

和77的区别是这个是回溯的if条件的不同，这里是小于等于，还有就是不能有return。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> subsets(int[] nums) {
        backtrack(nums, 0);
        return result;

    }
    public void backtrack(int[] nums, int startindex) {
        if (path.size() <= nums.length) {
            result.add(new ArrayList<>(path));
            //这里不能写return;否则出错，有return说明要终止本层的递归，我们要取树上的节点
        }
        for (int i = startindex; i < nums.length; i++) {
            path.add(nums[i]);
            backtrack(nums, i + 1);
            path.removeLast();
        }
    }
}

90 子集2 medium

遇到这个重复元素的，想都不用想，先排序，然后再处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        backtrack(nums, 0);
        return result;
    }
    public void backtrack(int[] nums, int startindex) {
        if (path.size() <= nums.length) {
            result.add(new ArrayList<>(path));
            //不要有return哦，否则会终止本层递归，我们要取树上的节点
        }
        for (int i = startindex; i < nums.length; i++) {
            if (i > startindex && nums[i - 1] == nums[i]) {//子集不能有重复的
                continue;
            }
            path.add(nums[i]);
            backtrack(nums, i + 1);
            path.removeLast();
        }

    }
}

491 递增子序列 medium

这个题不能排序，要用到原数组的顺序，所以可能会出现[4,6,4,7]这种数组，所以上一题子集不能重复的代码思想不能用到，要用map要判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        backtrack(nums, 0);
        return result;
    }
    public void backtrack(int[] nums, int startindex) {
        if (path.size() > 1) {//因为是递增子集，所以必须要有至少两个数才可以
            result.add(new ArrayList<>(path));
        }

        HashMap<Integer, Integer> map = new HashMap<>();//for循环中用map来记录使用过的数字次数，避免最后由重复子集。

        for (int i = startindex; i < nums.length; i++) {
            //满足递增子集，所以上一个数要是大于下一个数就去掉，还有就是这个数有重复用也去掉
            if (!path.isEmpty() && nums[i] < path.getLast() || map.getOrDefault(nums[i], 0) >= 1) {
                continue;
            }

            map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);//用了这个数就加1
            path.add(nums[i]);
            backtrack(nums, i + 1);//i+1纵向遍历不能重复的
            path.removeLast();
            //这里不需要map减去之前用过的数哦，我的理解是这个主要是因为用在for循环的横向遍历中，要是这里减1会出现重复的子集，可以对比下target那些题。
        }

    }
}

if条件也可以写成这样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public void backtrack(int[] nums, int startindex) {
    if (path.size() > 1) {
        result.add(new ArrayList<>(path));
    }

    HashMap<Integer, Integer> map = new HashMap<>();

    for (int i = startindex; i < nums.length; i++) {

        if (!path.isEmpty() && nums[i] < path.getLast()) {
            continue;
        }
        if (map.getOrDefault(nums[i], 0) >= 1) {
            continue;
        }//这里是区别哦

        map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
        path.add(nums[i]);
        backtrack(nums, i + 1);
        path.removeLast();
    }

}

46 全排列 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path= new LinkedList<>();
    public List<List<Integer>> permute(int[] nums) {
        backtrack(nums);
        return result;
    }
    public void backtrack(int[] nums) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {//和组合的区别1
            if (path.contains(nums[i])) {//和组合的区别2
                continue;
            }
            path.add(nums[i]);
            backtrack(nums);
            path.removeLast();
        }
    }
}
1
2
3
4
5
6
7
8
讲解组合和排列的区别
组合也就是[1,2,3]和[1,3,2]是一样的
而排列则视为他们是两个不同的结果。

所以在组合问题中使用了startindex来控制横向遍历中的重复元素问题
而排列则不需要，因为我们还会使用以前用过的数字，所以排列的时候，for就是全体元素的遍历，但是用过的数是不能用的，所以用path.contains来排除

这也是组合和排列的区别啦

47 全排列2 medium

这题的数组中可以有重复的数字，那么又如何去重呢？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/*
和40题一样的是，需要先进行排序
解决横向遍历中的重复数字i > 0 && nums[i - 1] == nums[i]也想到了
但是这里是全排列问题，在纵向遍历中会重复，所以这里需要用到一个used的数组
不过这个题不好理解
*/
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    boolean[] used;
    public List<List<Integer>> permuteUnique(int[] nums) {
        Arrays.sort(nums);
        used = new boolean[nums.length];
        Arrays.fill(used, false);
        backtrack(nums);
        return result;
    }
    public void backtrack(int[] nums) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        //used[i -1] == false说明同⼀树层nums[i - 1]使⽤过
        for (int i = 0; i < nums.length; i++) {
            if (i > 0 && nums[i - 1] == nums[i] && used[i -1] == false) {//这里的used[i -1] == false也能填true，但是代表两个意思，具体看卡哥解释
                continue;
            }
            if (used[i] == false) {//如果同⼀树⽀nums[i]没使⽤过开始处理
                used[i] = true;//标记
                path.add(nums[i]);
                backtrack(nums);
                path.removeLast();
                used[i] = false;//取消标记
            }
        }
     }
}

332 重新安排行程 hard

51 N皇后 hard

21 解数独 hard

贪心算法

455 分发饼干 easy

思路很简单，一个for循环就行，先排序，小饼干分给小胃口，然后注意越界问题就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int count = 0;
        int j = 0;
        for (int i = 0; i < s.length; i++) {
            if (j < g.length && s[i] >= g[j]) {//必须j < g.length放前面，先判断超界问题，这个是可能忘记的，因为饼干数量和小朋友数量不一定是一样的
                count++;
                j++;
            } 
        }
        return count;
    }
}

376 摆动序列 medium

可动态规划，要明确返回的是原始序列的长度哦，但是这个原始序列不一定就是题目给的全体，可能是子序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int wiggleMaxLength(int[] nums) {
        int pre = 0;
        int cur = 0;
        int result = 1;//初始化是1，至于为什么，可以理解下[1,1]这个数组，最后返回是数量2
        for (int i = 1; i < nums.length; i++) {//从头到尾进行遍历，注意因为要第二个数减去第一个数，所以从1开始
            cur = nums[i] - nums[i - 1];
            if ((cur > 0 && pre <= 0) || (cur < 0 && pre >= 0)) {
                result++;
                pre = cur;//要在if中加，这样才能保留上一个坡，而不是在if外围加
            }
        }
        return result;
    }
}

53 最大子数组和 medium

可动态规划，这里不要太关注数组下标，一开始老想着这个left和right，和209进行一个对比（这个题是算长度，以及人家有目标值），要注意是连续的子区间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int maxSubArray(int[] nums) {
        int result = Integer.MIN_VALUE;
        int count = 0;
        for (int i = 0; i < nums.length; i++) {
            count += nums[i];
            if (count > result) {
                result = count;
            }
            if (count < 0) {
                count = 0;
            }
        }
        return result;
    }
}
1
2
3
4
5
6
7
如果 -2 1 在一起，计算起点的时候，一定是从1开始计算，因为负数只会拉低总和，这就是贪心贪的地方！

利用两个数来完成这个题，result来记录最大的值，同时也是结果值，而count是记录区间的值

我们要知道最大和，意味着我们不能加上负数，否则只会越来越小，而count是记录区间的大小，当区间大小为负数的时候，我们就不要这个区间了，在下个位置重新开始记录初始化为0，在这个过程中一直对比最大值即可。

和209的区别，209是求最小的长度，而且是有targer的，当和大于等于这个targer后在慢慢看最小的长度，而本题是计算和

122 买卖股票的最佳时机II medium

可动态规划，贪心思想：局部最优：收集每天的正利润，全局最优：求得最大利润。

1
2
3
4
5
6
7
8
9
class Solution {
    public int maxProfit(int[] prices) {
        int result = 0;
        for (int i = 1; i < prices.length; i++) {
            result += Math.max((prices[i] - prices[i - 1 ]),0);
        }
        return result;
    }
}

55 跳跃游戏 medium

贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public boolean canJump(int[] nums) {
        if (nums.length == 1) return true;
        int cover = 0;//这里是cover是值步数，而这个步数能否覆盖到最后即可判断为true。
        for (int i = 0; i <= cover; i++) {//注意这里是cover 不是nums的长度，因为cover初试值是0，所以要小于等于哦
            cover = Math.max(i + nums[i], cover);//cover是会改变的
            if (cover >= nums.length - 1) return true;//cover是对应数组下标，所以nums的长度-1
        }
        return false;
    }
}

45 跳跃游戏2 medium

和上一题的区别是这题要算出一个最小的步数，只需要考虑覆盖的范围是不是到最后一个，而本题没那么简单。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/*
这里解释为什么循环是nums.length - 1而不是nums.length
在遍历数组时，我们不访问最后一个元素，这是因为在访问最后一个元素之前，我们的边界一定大于等于最后一个位置，否则就无法跳到最后一个位置了。如果访问最后一个元素，在边界正好为最后一个位置的情况下，我们会增加一次「不必要的跳跃次数」，因此我们不必访问最后一个元素。

假设我们就是nums.length，用案例[2,3,1,1,4]
那么最大范围是下标会是 2（第一次可以跳的下标范围） 4（第二次可以跳的下标范围） 8，其实在第二步4的时候已经到了最后了，但是又多跳一步，然后最大范围可以是8，也就是避免刚好到了末尾又跳

*/
class Solution {
    public int jump(int[] nums) {
        int end = 0;//上次跳跃可达范围右边界（下次的最右起跳点）
        int maxcount = 0;//目前能跳到的最远位置
        int step = 0;//跳跃次数
        for (int i = 0; i < nums.length - 1; i++) {//注意上一题的循环变量是cover
            maxcount = Math.max((i + nums[i]), maxcount);//取最大的范围
            if (i == end) { // 到达上次跳跃能到达的右边界了
                end =  maxcount;// 目前能跳到的最远位置变成了下次起跳位置的有边界
                step++; // 进入下一次跳跃
            }
        }
        return step;
    }
}

1005 K 次取反后最大化的数组和 easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/*
思路就是让最小的负数的开始取反(排序)

如果所有的负数已经取反了，但是k还是大于0，那就让重新排序，让前面小的值来取反，每次都要重新排序

最后求和
*/
class Solution {
    public int largestSumAfterKNegations(int[] nums, int k) {
        Arrays.sort(nums);
        int result = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] < 0 && k > 0) {
                nums[i] = -nums[i];          
                k--;
            }
        }
        
        while (k > 0) {
            Arrays.sort(nums);
            for (int i = 0; i < k; i++) {//小于k哦
                nums[i] = -nums[i];
                k--;
            }
        }

        for (int x : nums) {
            result += x;
        }
        return result;

    }
}

134 加油站 medium

要充分利用贪心的思想。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/*
思路如下，设置两个变量totalsum和cursum。
totalsum就是全部的加油量减去耗油量，如果大于0，说明是可以跑完一圈的
然后在这个的基础上，我们可以去找开始出发点，利用到cursum，这个变量就是从[i,j]范围内的加油量减去耗油量，如果是负数的话，我们的起始点就设置为下一个数，然后重新计算cursum
我一开始在想的时候，会考虑到cost[i]是去第i+1个的耗油量，cursum里面是计算gas[i]-cost[i]，所以会不会不对应呢，其实不会的
比如gas是[3,4]，cost是[4,2]，你如果在0号，那么cursum就是-1.也就是说当前加的油不够去下一站，所以这个是对应上的，那么这个起始点就不能选择，所以就移动一位检查下一个起始点，务必注意cursum要重新置0。 
*/
class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int cursum = 0;
        int totalsum = 0;
        int start = 0;
        for (int i = 0; i < gas.length; i++) {
            cursum += gas[i] - cost[i];
            totalsum += gas[i] - cost[i];
            if (cursum < 0) {
                cursum = 0;
                start = i + 1;
            }  
        }
        if (totalsum < 0) return -1;
        return start;

    }
}

135 分发糖果 hard

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/*
领悟的关键，更新的时候能不能用上新的值来比较，遇到两个维度权衡的时候，一定要先确定一个维度，再确定另一个维度。

这里需要注意从前往后遍历，需要用右边来对比左边，然后更新右边的值，那么下一次循环再对比，原来右边的值变成左边，这时候再进行右边是否大于左边去更新，因为这时候左边的值是新值，是有意义的
如果我们来更新左边的值，比如左边大于右边，然后更新左边的值，到了下一次循环，下一次的左边是一个旧值，没有意义，我们用不到新的值

然后处理完左边循环（右比左大），然后处理从右边开始的循环，左边比右边大，更新左边的值（注意这时候不是右边原来的值加1，不然会破坏原来前序遍历的结果），需要取就取candys[i + 1] + 1 和 candys[i] 最大的糖果数量
比如举个例子[1,3,4,5,2]，前序遍历完后糖果数组是[1,2,3,4,1]，如果你这时候用candys[i+1]+1更新的话，就变成[1,2,3,2,1]，第四个位置就乱套了，所以取他们的最大值即可
*/
class Solution {
    public int candy(int[] ratings) {
        int[] candys =  new int[ratings.length];
        int result = 0;
        Arrays.fill(candys,1);
        for (int i = 1; i < ratings.length; i++) {
            if (ratings[i] > ratings[i - 1]) {//右边比左边大
                candys[i] = candys[i - 1] + 1;
            }
        }
        for (int i = ratings.length - 2; i >= 0; i--) {
            if (ratings[i] > ratings[i + 1]) {//左边比右边大
                candys[i] = Math.max(candys[i], candys[i + 1] + 1);
            }
        }
        for (int x : candys) {
            result += x;
        }
        return result;

    }
}

860 柠檬树找零 easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/*
别看代码特多逻辑判断，其实很简单，就三种情况
1.付款5元的，直接收取，记录5元张数
2.付款10元的，只能找5元，记录10元张数，同时找5元（减张数），如果不够找，直接返回false
3.付款20元的，可以找10元和5元的，也可以纯5元的，这时候就判断够不够找，不够也返回false
最后别忘了返回true
*/
class Solution {
    public boolean lemonadeChange(int[] bills) {
        int five = 0;
        int ten = 0;
        int twenty = 0;//其实也可以不用这个参数
        int temp = 0;
        for (int i = 0; i < bills.length; i++) {
            temp = bills[i] / 5;
            if (temp == 1) {
                five++;
            } else if (temp == 2) {
                if (five < 0) return false;
                ten++;
                five--;
            } else {
                twenty++;
                if (ten > 0 && five > 0) {
                    ten--;
                    five--;
                } else if (five >= 3) {
                    five = five - 3;
                } else return false;
                }
            }
        return true;
    }
}

406 根据身高重建队列 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/*
思想就是先排序（高到低排），再插队（下标就是插入的位置），至于为什么，这是贪心的思想，数学证明很难哦，局部最优做到总体最优，矮个子排在哪都对高个子没有影响，但是高个子排在矮个子前面就会造成影响。所以，矮个子要主动选择位置
*/
class Solution {
    public int[][] reconstructQueue(int[][] people) {
        Arrays.sort(people,(a, b) -> {
            if (a[0] == b[0]) return a[1] - b[1];
            return b[0] - a[0];
        }
        );//这里有分号
        LinkedList<int[]> que = new LinkedList<>();
        for (int[] p : people) {//这里是people哦
            que.add(p[1],p);
        }
        return que.toArray(new int[people.length][]);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
输入是[[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]，最终结果是[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
这里好多语法是第一次见，详细记录一下
if (a[0] == b[0]) return a[1] - b[1];//如果身高相同，就按照比他高的人数进行升序排序，也就是第二个位置的数进行由小到大排
return b[0] - a[0];//否则身高不相同，就按照逆序排，也就是从高到矮排

a和b分别代表第一个数组和第二个数组
0和1就是这个数组的身高和比他高的人数


LinkedList.add(int index,E elemnt)//add(索引位置,待插入元素)
也就是按照数组第二个位置进行插入即可

将que转成数组，下面是打印出第一个数的情况
int[][] res = que.toArray(new int[people.length][]);
System.out.print(Arrays.toString(res[0]));//输出是[5, 0]
二维数组可以不定义列数，但必须定义行数。

452 用最小数量的箭引爆气球 medium

学习下这个二维数组的排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/*
先理解为什么要排序，可以理解为这个数组的顺序只是告诉你他们的位置而已
然后要知道，一只箭射的是可以重叠的区间

首先获得第一个气球的右边界
然后循环判断，如果下一个气球的左边界比上一个气球的右边界还小（等于也行），说明他们是重叠的，可以用一只箭，然后更新这个右边界的值
为什么要更新这个右边界的值呢，怎么更新呢？
如果第一个区间是[0,100]，那么初试的右边界是100,第二个区间是[3,4],他们可以用一只箭，但是如果第三个区间是[5,6]，需要新箭了，因为[3,4]和[5,6]不重叠，不能用一只箭
所以更新区间的策略是用最大右边界的值和当前区间的右边界值进行比较，取小的那个

这个题要纵向看，如下图所示
然后接着下一个区间，判断左边界和比最大右边区间
*/
class Solution {
    public int findMinArrowShots(int[][] points) {
        if (points.length == 0) return 0;
        Arrays.sort(points, (a, b) -> Integer.compare(a[0],b[0]));
        /*
        //用x[0] - y[0] 会大于2147483647 造成整型溢出
        Arrays.sort(points,(a, b) -> {
            return a[0] - b[0];
        });
        */
        int count = 1;//因为无论如何至少有一支箭
        int rightedge = points[0][1];

        for (int i = 1; i < points.length; i++) {
            if (points[i][0] > rightedge) {
                count++;
                rightedge = points[i][1];
            } else {
                rightedge = Math.min(rightedge, points[i][1]);
            }
        }
        return count;
    }
}

435 无重叠区间 medium

去掉重叠的区间，[1,2],[2,3]不算重叠，然后计算需要去掉的个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/*
和上个题很像，但是这个题是去除重叠的区间，计数即可，不需要返回去除后的区间

思路是左边区间从小到大排序
然后取第一个数组的右边区间作为右边界rightedge

开始循环，如果第二个数的左边区间小于rightedge，说明重叠了，这时候要count++，至于移除哪个，你不需要纠结，你计数即可，然后重新取右边区间

可以看到，这个题和上一题的逻辑 是有点相反的！

第二次做的反思：关于min的问题，这里是相交的时候取最小的右边，二个数的左边区间小于rightedge，重叠，肯定要移除一个，但是为什么保留较小的右边呢，因为如果你的rightedge很大的话，说明很多区间是可能发生重叠的，所以才是这个道理
*/
class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
        int rightedge = intervals[0][1];
        int count = 0;//和上一题不同哦，这里是计算去掉区间的个数
        for (int i = 1; i < intervals.length; i++) {
            if (intervals[i][0] < rightedge) {//现在数组的左区间小于右边界，说明有重叠，需要去掉
                count++;
                rightedge = Math.min(rightedge, intervals[i][1]);
            } else {
                rightedge = intervals[i][1];
            }

        }
        return count;
    }
}

763 划分字母区间 medium

字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/*
我们需要输出的是每个片段的长度

注意是尽可能多的片段，然后相同字母都在一起，不然要最少片段，就不用分割了

方法就是
1.统计每一个字符最后出现的位置
2.从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点
*/
class Solution {
    public List<Integer> partitionLabels(String s) {
        List<Integer> list = new LinkedList<>();
        int[] edge = new int[26];
        char[] chars = s.toCharArray();//把字符串分割成一个个字符
        for (int i = 0; i < s.length(); i++) {
            edge[chars[i] - 'a'] = i;//不断更新该字符的最远距离，存进edge中
        }
        int last = -1;//初始化-1是为了减的时候多加一个1，因为我们要返回个数
        int index = 0;//用来标记最远距离
        for (int i = 0; i < s.length(); i++) {
            index = Math.max(index, edge[chars[i] - 'a']);//获取该字符的最远距离，进入第二轮的话就是和上一个相比
            if (index == i) {//如果当前位置刚好就是这个距离，就说明找到分割点了
                list.add(i - last);//计算长度
                last = i;//更新last，准备下一次计算
            }
        }
        return list;
    }
}

56 合并区间 mediun

这个题注意下返回的输出格式。注意[1,4],[4,5]也要合并的，变成[1,5]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int[][] merge(int[][] intervals) {
        List<int[]> result = new LinkedList<>();
        Arrays.sort(intervals, (a ,b) -> Integer.compare(a[0], b[0]));

        int leftedge = intervals[0][0];
        int rightedge = intervals[0][1];

        for (int i = 1; i < intervals.length; i++) {
            if (intervals[i][0] > rightedge) {//左边区间大于的上一个数的右边界，说明可以把之前的边界合并在一起了
                result.add(new int[]{leftedge, rightedge});
                leftedge = intervals[i][0];
                rightedge = intervals[i][1];
            } else {//这个就是小于等于号的情况
                rightedge = Math.max(intervals[i][1], rightedge);
            }
        }
        result.add(new int[]{leftedge, rightedge});//上面的数循环完后，会漏掉最后一个区间的，所以最后加上
        return result.toArray(new int[result.size()][]);
    }
}

上面452,435,56题，需要好好理解什么时候是需要比较max的右边界的，而且上面三个题，都是左边区间排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
别忘了均是左边区间排序，从小到大，还有循环都是从1开始

452 
在右边界内，也就是当前数组的左边区间小于右边界，说明重叠了，可以穿过同一只箭，不需要更新箭的数量，但是这时候要更新右边区间，要缩小右边区间的范围，所以要用min来对比
反之如果大于这个右区间，就要增加箭的数量，然后更新右边界

435
去掉重叠的区间注意[1,2][2,3]不重叠
在右边界内，也就是当前数组的左边区间小于右边界，说明需要去掉一个数组，count++，同时需要更新右边界min来比较，为什么要min呢，可以这么想，万一第一个的右边界很大，覆盖了全部数组，那必须得去掉啊
如果不在边界，就直接更新右边界的值即可


56
注意[4,5]，[5,6]也是需要合并的
这个题要记录左右边界
在右边界外，也就是当前数组的左边区间大于右边界，可以直接添加元素了，为什么不用小于等于呢（别忘了上面一行什么情况需要合并），其实也可以的，只是里面内容不一样而已，添加了元素后，要更新左右边界
反正，只需要更新右边界，因为不确定下一个是不是还是重叠的，所以这里不添加元素，只是改变右边界
循环完后，会漏掉最后一个区间的，所以最后加上
这个题的的返回值要注意下

动态规划

1
2
3
4
5
1.确定dp[i]的含义
2.确定递推公式（转移方程）
3.初始化dp数组
4.确定遍历顺序
5.举例推导dp数组

509 斐波那契数 easy

1
2
3
4
5
6
7
1.dp[i] 第i个数的斐波那契数
2.转移方程 dp[i] = dp[i - 1] + dp[i - 2];
3.初始化dp[0],dp[1]
4.dp[i]依赖dp[i-1]和dp[i-2]，按照顺序遍历
5.自己推导一下0 1 1 2 3 5 8 13 21 34 55

这里注意一个点就是求dp[n]，也就是初始化数组的大小是n+1
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int fib(int n) {  
        if (n < 2) return n;  
        int[] dp = new int[n + 1];//这是需要注意理解题目的
        dp[0] = 0;
        dp[1] = 1;

        for (int i = 2; i <= n; i++ ) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

70 爬楼梯 easy

1
2
3
4
5
6
7
8
先理解题目，每次可以爬两级或者爬一级，也就是你可以在dp[i-2]的级上爬两级，也可以在dp[i-1]的级上爬一级，那么爬楼梯的方法就有dp[i-1]加上dp[i-2]
本题不需要dp[0]，因为这样没有意义，没有说爬0级的楼梯，所以dp[1]和dp[2]需要初始化，由于是求dp[n]，所以数组的长度也就是需要n+1

1.dp[i]爬到第i层楼梯的方法数
2.根据我上面写的题意可以推出 dp[i]=dp[i-1]+dp[i-2]
3.第0层没意义，但是会生成数组的时候会自动初始化0，我们也不需要管，dp[1]=1,dp[2]=2
4.dp[i]依赖dp[i-1]和dp[i-2]，按照顺序遍历
5.可以自己推导下前面几个，比如 1 2 3 5 8
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int climbStairs(int n) {
        if (n < 3) return n;  
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

746 使用最小花费爬楼梯 easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
这个题需要好好看看讲解哦，本题的要求是花费最小的体力值，然后首先看下面的例子理解下顶部是哪里！！！这个一开始我很懵，跟70一样，也是一次可以跳1级或者2级
例子1：cost = [10,15-,20]，支付 15 ，向上爬两个台阶，到达楼梯顶部，顶部这里是没有体现的，也就是跳到cost[2]是一级，然后再跳到顶部是一级，一共两级

这里-标记了跳的台阶

例子2：cost = [1-,100,1-,1,1-,100,1-,1-,100,1-],一共支付6，从下标为0的台阶开始
- 支付 1 cost[0]，向上爬两个台阶，到达下标为 2 的台阶。
- 支付 1 cost[2]，向上爬两个台阶，到达下标为 4 的台阶。
- 支付 1 cost[4]，向上爬两个台阶，到达下标为 6 的台阶。
- 支付 1 cost[6]，向上爬一个台阶，到达下标为 7 的台阶。
- 支付 1 cost[7]，向上爬两个台阶，到达下标为 9 的台阶。
- 支付 1 cost[9]，向上爬一个台阶，到达楼梯顶部。

看到题目的例子后，需要注意，最后一个楼梯顶部，在数组中是没有体现他的位置的，也就是后移一个，其实不需要纠结这个问题
因为你只要最后取数组倒数两个进行比较就行，哪个花费体力小就用哪个，这样他们都可以跳到楼顶

1.dp[i]到达第i个台阶需要花费的最少体力
2.因为我们需要花费最少的体力，然后可以跳1级或者2级，也就是 dp[i]=dp[i-1]+dp[i-2]
3.初始化2个就行，dp[0]和dp[1]
4.dp[i]依赖dp[i-1]和dp[i-2]，按照顺序遍历
5.推导一下cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的dp数组是[1,100,2,3,3,103,4,5,104,6]

这里的转移方程详细说下，dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
这里为什么是cost[i]而不是cost[i-1]或者cost[i-2]
因为我们想，我们现在是取到了前面两个比较小的值，然后本级需要跳，就要花费，先不考虑我们这个级跳1级还是2级的问题，因为我们先把整个dp数组弄出来，最后比较最后两个的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        if (cost == null || cost.length == 0) {
            return 0;
        }
        if (cost.length == 1) {
            return cost[0];
        }
        int[] dp = new int[cost.length];
        dp[0] = cost[0];
        dp[1] = cost[1];
        for (int i = 2; i < cost.length; i++) {
            dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
        }
        return Math.min(dp[cost.length - 2], dp[cost.length - 1]);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        /*这部分可以不写，因为不存在这个范围的用例
        if (cost == null || cost.length == 0) {
            return 0;
        }
        if (cost.length == 1) {
            return cost[0];
        }
        */
        int[] dp = new int[cost.length];
        dp[0] = cost[0];
        dp[1] = cost[1];
        for (int i = 2; i < cost.length; i++) {
            dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
        }
        return Math.min(dp[cost.length - 2], dp[cost.length - 1]);
    }
}

62 不同路径 medium

1
2
3
4
5
1.dp[i][j]代表到从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。
2.题目说只能从右边还有下边走，所以只依赖两个方向的路径，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
3.dp初始化，第一行和第一列的坐标都是1，因为只有一个方向走
4.遍历顺序就是从左到右
5.自己手动画下推导数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int [m][n];
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
}

63 不同路径2 medium

1
2
3
4
5
6
7
8
和上一题五部曲差不多，这里直说区别

首先初始化问题
初始化只在第一行和第一列，但是如果遇到障碍，需要break，而不是continue，这个的意思是，障碍后面的格子，都是0了，但是如果你是continue的话，只是单纯障碍这一格子是0，但是后面是1
而我们需要知道，你只要有障碍，后面都不能通过了


在具体递推公式的时候，遇到障碍则跳过，不是break，因为你break的话就全部结束了，而continue只是跳过这个格子，这样这个格子就会为0，在其他位置需要加他的时候，就是加0。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++) {
            if (obstacleGrid[i][0] == 1) break;
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            if (obstacleGrid[0][i] == 1) break;
            dp[0][i] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 1) continue;
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
}

343 整数拆分 medium

1
2
3
4
5
6
7
8
这个题感觉没那么容易理解

1.dp[i] 分拆数字i，可以得到的最大乘积为dp[i]。
2.当i>=2 时，假设对正整数 i 拆分出的第一个正整数是 j（1<=j<i），则有以下两种方案：1.将 i拆分成j和i−j的和，且i−j 不再拆分成多个正整数，此时的乘积是j*(i-j)；2.将 ii 拆分成 jj 和 i-ji−j 的和，且 i-ji−j 继续拆分成多个正整数，此时的乘积是j*dp[i-j]。
上面其实不容易懂，需要这样理解，j * (i - j) 是单纯的把整数拆分为两个数相乘，而j * dp[i - j]是拆分成两个以及两个以上的个数相乘，因为题目要求可以至少拆分出2个。
3.首先要清楚，dp[0]和dp[1]，因为0无法拆分，1也无法拆分，所以初始化要从2开始，2=1+1，然后1*1=1，dp[2]=1，然后注意数组长度是n+1
4.遍历顺序也是第一次见，需要i和j，然后也是顺序遍历
5.自己可以手动推导，比如n=10，dp数组是1,2,4,6,9,12,18,27,36
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n + 1];
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j <= i - j; j++) {//这里j的范围需要注意是小于等于i-j
                dp[i] = Math.max(dp[i], Math.max(j * (i - j), dp[i - j] * j));
            }
        }
        return dp[n];
    }
}

96 不同的二叉搜索树 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
这个题其实算困难了，尤其是递推关系，没做过压根不知道，可以看卡哥的图

1.dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]
2.递推公式
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]
有1个元素的搜索树数量就是dp[1]
有0个元素的搜索树数量就是dp[0]
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

递推公式：dp[i] += dp[j - 1] * dp[i - j]
这个不好记，可以看dp[3]，第一个是dp[2]*dp[0]，i=3，然后j是从1开始，所以可以想到i-j,然后另外一个规律就是2+0=2，前面3-1=0，另外一个就是j-1=0，此时j=1哦

3.dp[0] = 1，dp[1]=1,1的话好理解，但是0的话不好理解，但是我们后面用到乘法，所以初始化为1更好。
4.节点数为i的状态是依靠 i之前节点数的状态，从前往后即可
5.可以推导下
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <=n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[i - j] * dp[j - 1];
            }
        }
        return dp[n];
    }
}

416 分割等和子集 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0-1背包问题
nums里面可以看成物品，每个物品只能用一次，题目拆解后可以发现target是背包容量

对于一维dp数组，务必先遍历物品，反正倒着遍历容量（因为每次元素不能重复使用），其次还要注意j>=nums[i]，而不是0

这里 dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
max中的dp[j]可以理解为二维数组中的dp[i-1]，因为如果用一维数组dp[i - 1]那一层拷贝到dp[i]上

五部曲
1.dp[j]表示容量为j的背包，所背物品价值最高是dp[j]
2.dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);本题的物品，既是容量，也是价值
3.题目给的价值都是正整数的话，都可以初始化为0
4.遍历顺序：使用一维数组的话，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！
5.自己递推试试，注意本题的容量是target，所以数组的长度是target+1

这里有个细节就是，target可能不能被整除，所以先要判断能不能被2取模
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int x : nums) {
            sum += x;
        }
        if (sum % 2 != 0) return false;//很细的细节
        int target = sum / 2;
        int[] dp = new int[target + 1];
        for (int i = 0; i < nums.length; i++) {
            for (int j = target; j >= nums[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            }
        }
        return dp[target] == target;
    }
}

1049 最后一块石头的重量II medium

1
2
3
4
5
6
7
这个题和上个题的区别是，上个题能不能正好装满，这个题是求最多能装多少
其实一开始看这个题，有点懵，一直纠结一直拿两块石头应该怎么拿。
看了分析后，其实这个题的本意是尽量让石头分成重量相同的两堆，这样相撞后的石头最小。同样，本题物品的重量为store[i]，物品的价值也为store[i]。
也就是当我们把所有重量求和/2，就可以求我们的dp数组，然后这个题不需要考虑sum能否被整除2，因为本题说了是最多能装多少
最后，我们理解下题目需要返回什么，按照上面的思路，其实石头被分成两堆，一堆是dp[target]，一堆是sum-dp[target],然后相减就是剩下石头的重量

五部曲和上面一题一样
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        for (int x : stones) {
            sum += x;
        }
        int target = sum / 2;
        int[] dp = new int[target + 1];
        for (int i = 0; i < stones.length; i++) {
            for (int j = target; j >= stones[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
            } 
        }
        return sum -  2 * dp[target];
    }
}

494 目标和 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
涉及组合问题，而且这个题和其他背包问题不太一样，有点难度，下面详细讲下，本题也是0-1背包。

首先理解一点是如何表达target
我们可以计算出这个数组的总和sum，然后我们想想都是加号的数字和为a，都是减号的数字和为b，
那么a-b就是sum，然后a+b就是target(这里和卡哥有点出入，我按照自己的理解去写，他是反过来的)
b= a-sum 
a+a-sum=target
a=(target+sum)/2

a即为bagsize
这里需要考虑2个问题，一个是target的绝对值如果大于sum，是不可能组成的，因为可能有这种案例
第二个考虑就是(target+sum)%2==1的话，也是不行的，例如sum 是5，target是2的话其实就是无解的，根本无法组合出来，4-1=3,3-2=1，压根组合不到2，也就是要求sum+target一定为偶数才行，至于为啥，还没想通。

那么这里a就可以理解为背包容量，为什么呢，我们理解为组成加号和为a情况有多少种
那么dp[a+1]，这是dp数组长度


五部曲
1.dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法
2.这里的递推公式不一样！！！！其实也不算完全理解
不考虑nums[i]的情况下，填满容量为j的背包，有dp[j]种方法。
那么考虑nums[i]的话（只要搞到nums[i]），凑成dp[j]就有dp[j - nums[i]] 种方法。
例如：dp[j]，j 为5
已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 dp[5]。
已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 dp[5]。
已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 dp[5]。
已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 dp[5]。
已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 dp[5]。
那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。
这个是组合类问题，递推公式为：dp[j] += dp[j - nums[i]]
3.初始化
这里必须要设置dp[0]为1，这个可以理解为容量为0的背包，有一种方法，就是装0件物品。但是如果初始化是0后面无法推导。
4.遍历顺序，物品放外面（数组），容量放里面（bagsize）。
5.推导数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for (int x : nums) {
            sum += x;
        }
        if ((sum + target) % 2 == 1) return 0;
        if (Math.abs(target) > sum) return 0;
        int bagsize = (sum + target) / 2;
        int[] dp = new int[bagsize + 1];
        dp[0] = 1;
        for (int i = 0; i < nums.length; i++) {
            for (int j = bagsize; j >= nums[i]; j--) {
                dp[j] += dp[j - nums[i]];
            }
        }
        return dp[bagsize];
    }
}

474 零和一 medium

1
2
3
4
5
6
7
8
9
这个题 也没那么容易，本质也是0-1背包问题

sts数组就是物品，然后这里很难理解的就是m和n，这里不能理解为多重背包，这里要理解为有两个维度的背包。

1.dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]，也就是里面存的是大小
2.dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
3.初始化就是0
4.遍历顺序，这个题有点不一样哦，里面是两个维度的容量，但是总体上还是物品在外面遍历，容量在里面遍历（倒着）
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int[][] dp = new int[m + 1][n + 1];
        for (String str:strs) {//物品，也就是每个数组
            int onenum = 0, zeronum = 0;//每次都要重新计算数组的0和1的个数
            for (char c : str.toCharArray()) {
                if (c == '0') {
                    zeronum++;
                } else {
                    onenum++;
                }
            }
            //下面是容量，注意题目m是代表0，n是代表1，不需要搞错了
            for (int i = m; i >= zeronum; i--) {
                for (int  j = n; j >= onenum; j--) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeronum][j - onenum] + 1);
                }
            }            
        }
        return dp[m][n];
    }
}

背包问题解析合集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
总结一下，0-1背包物品先，容量倒着来，完全背包物品先，容量顺着来
组合问题物品先，容量顺着来，排列问题容量先从头来

至于是写dp[j]还是dp[i]，是根据你把j和i定义成什么，其实都是dp[容量],也就是用容量的下标来表示


1.   0-1背包
表示物品只能拿一次，先遍历物品（顺序），再遍历容量（倒着，保证物品只被添加一次）
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}
倒着的原因，这里举个例子
    重量  价值
物品0 1   15
物品1 3   20
物品2 4   30

如果是正序遍历
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[0] = 30
我们可以看到dp[2]这样是加了两次物品0的重量

但是如果是倒序遍历
dp[2] = dp[2 - weight[0]] + value[0] = 15 （dp数组已经都初始化为0）
dp[1] = dp[1 - weight[0]] + value[0] = 15

最后再次说明dp[j]的意思是容量为j的背包，所背的物品价值可以最大为dp[j]。

2.   完全背包
表示物品可以添加多次，先遍历物品（顺序），再遍历容量（顺序，可以添加多次）
// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量，顺序遍历，顺序遍历
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

另外说一些额外的：
01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。
完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序同样无所谓！但是代码还是有点不一样，这里就看个参考，不要记了
// 先遍历背包，再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量，别忘了，这里是j
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
    cout << endl;
}


3.   组合数和排列数问题，组合不强调元素之间的顺序（也就是[1,5]和[5,1]是一回事），排列强调元素之间的顺序，初始化dp[0]为1，至于为什么，没有原因。
494是组合问题，初始化dp[0]为1

组合代码，和完全背包一样，都是先遍历物品，再遍历容量
for (int i = 0; i < coins.size(); i++) { // 遍历物品
    for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
        dp[j] += dp[j - coins[i]];
    }
}

排列代码 ，这个不一样哦，先遍历容量，再遍历，而且背包遍历容量，是从0开始的，注意背包
如果把遍历nums（物品）放在外循环，遍历target的作为内循环的话，举一个例子：计算dp[4]的时候，结果集只有 {1,3} 这样的集合，不会有{3,1}这样的集合，因为nums遍历放在外层，3只能出现在1后面！

for (int j = 0; j <= amount; j++) { // 遍历背包容量
    for (int i = 0; i < coins.size(); i++) { // 遍历物品
        if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];//注意要有背包容量大于等于coins[i]
    }
}

377 组合总和Ⅳ medium

这个其实是排列+完全背包问题

1
2
3
4
5
1.dp[i]: 凑成目标正整数为i的排列个数为dp[i]
2.求排列 dp[i] += dp[i - nums[j]];
3.dp[0] = 1，组合排列都是这样初始化，其他位置为0
4.外层for遍历背包，内层for循环遍历物品，且注意背包容量要大于物品，不然会越界
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp =new int[target + 1];
        dp[0] = 1;
        for (int j = 0; j <= target; j++) {//容量
            for (int i = 0; i < nums.length; i++) {//物品
                if (j - nums[i] >= 0) dp[j] += dp[j - nums[i]]; //且注意背包容量要大于物品，不然会越界
            }
        }
        return dp[target];
    }
}

518 零钱兑换II medium

完全背包+组合，注意这里是求凑成总金额的硬币组合数。

1
2
3
4
5
1.dp[j]：凑成总金额j的货币组合数为dp[j]
2.组合数，dp[j] += dp[j - coins[i]]
3.dp[0] = 1，组合排列都是这样初始化，其他位置为0
4.顺序遍历物品（金币），顺序遍历容量（钱总额）
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount + 1];
        dp[0] = 1; 
        for (int i = 0; i < coins.length; i++) {//物品
            for (int j = coins[i]; j <= amount; j++) {//容量
                dp[j] += dp[j - coins[i]]; 
            }
        }
        return dp[amount];

    }
}

322 零钱兑换 medium

1
2
3
4
5
6
7
8
和上题的区别
本题求的是硬币的最小个数，最小的话，有顺序和没有顺序都可以，也就是排列组合都没有关系，但是符合完全背包（钱币可以无限用）

1.dp[j]：凑足总额为j所需钱币的最少个数为dp[j]
2.递推公式：dp[j] = min(dp[j - coins[i]] + 1, dp[j]);，其实这里我还没理解为啥加1
3.首先凑足总金额为0所需钱币的个数一定是0，那么dp[0] = 0;其次其他下标需要为最大值
4.完全背包，先遍历顺序物品，然后顺序遍历容量
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        for (int i = 0; i < coins.length; i++) {//物品
            for (int j = coins[i]; j <= amount; j++) {//容量
                if (dp[j - coins[i]] != Integer.MAX_VALUE) // 如果dp[j - coins[i]]是初始值则跳过
                    {dp[j] = Math.min(dp[j],dp[j - coins[i]] + 1);}//看了别人的解释，金额为11的最小硬币数 和 金额为(11-一个面值)的最小硬币数+1 比较最小值
            }
        }
        return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];//因为可能不能组合成功，那么就返回-1
    }
}

完全背包也可以先写容量，再写物品，但是要多加一个判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int [amount + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        for (int j = 1; j <= amount; j++) {//其实j从0开始也行的，但是我们之前声明了dp[0]，所以没意义，直接从1开始
            for (int i = 0; i < coins.length; i++) {
                if (j - coins[i] >= 0 && dp[j - coins[i]] != Integer.MAX_VALUE) dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
            }
        }
        return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];
    }
}

279 完全平方数 medium

和前面一题差不多，这里把完全平方数看做物品。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        for (int j = 1; j <= n; j++) {//容量
            for (int i = 1; i * i <= j; i++) {//物品，平方数是0没有意义，而且写0也会错的，自己推导一下就知道，这里直接是用i，而不是像数组那样
                /*if (j - i * i >= 0)  加上这句也是可以的*/ dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
            }
        }
        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        for (int i = 1; i * i <= n; i++) {//物品
            for (int j = 1; j <= n; j++) {//容量
                if (j - i * i >= 0) dp[j] = Math.min(dp[j], dp[j - i * i] + 1);//这里和之前总结的东西有点区别，为什么这里要if判断，有个原因就是这里是直接用i本身，而不是用数组
            }
        }
        return dp[n];
    }
}

139 单词拆分 medium

这道题类似于完全平方数分割。单词就是物品，字符串s就是背包，完全背包问题，求能否组成背包，因为分割子串的特殊性，遍历背包放在外循环，将遍历物品放在内循环更方便一些。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/*跟下面的解法一样的，只是习惯了j代表背包容量而已*/
class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        boolean[] dp = new boolean[s.length() + 1];//默认都是false的
        dp[0] = true;//dp[0]表示如果字符串为空的话，说明出现在字典里。
        for (int j = 1; j <= s.length(); j++) {//容量
            for (int i = 0; i < j; i++) {//物品
                if (wordDict.contains(s.substring(i, j)) && dp[i] == true) {//(j,i)，注意是j开始，这里表示起始位置，左开右闭，dp[j]==true表示字符串长度为j的话，可以拆分为一个或者多个在字典中出现的单词，也就是之前的单词都是能拆的，然后如果后面也能拆，再把dp[i]置为true
                    dp[j] = true;
                }
            }
        }
        return dp[s.length()];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        int n = s.length();
        boolean[] dp = new boolean[n + 1];//默认都是false的
        dp[0] = true;//dp[0]表示如果字符串为空的话，说明出现在字典里。
        for(int i = 1; i <= n; i++) {//容量
            for(int j = 0; j < i; j++) {//物品
                if(wordDict.contains(s.substring(j,i)) && dp[j] == true) { //(j,i)，注意是j开始，这里表示起始位置，左开右闭，dp[j]==true表示字符串长度为j的话，可以拆分为一个或者多个在字典中出现的单词，也就是之前的单词都是能拆的，然后如果后面也能拆，再把dp[i]置为true
                    dp[i] = true;
                }
            }
        }
        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
卡哥将得很详细，复制一下记录
单词就是物品，字符串s就是背包，单词能否组成字符串s，就是问物品能不能把背包装满。substring(start,end)是左开右闭。

拆分时可以重复使用字典中的单词，说明就是一个完全背包！

动规五部曲分析如下：

1.确定dp数组以及下标的含义
dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词。

2.确定递推公式
如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true。（j < i）。

所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。

3.dp数组如何初始化
从递归公式中可以看出，dp[i] 的状态依靠 dp[j]是否为true，那么dp[0]就是递归的根基，dp[0]一定要为true，否则递归下去后面都都是false了。

那么dp[0]有没有意义呢？

dp[0]表示如果字符串为空的话，说明出现在字典里。

但题目中说了“给定一个非空字符串 s” 所以测试数据中不会出现i为0的情况，那么dp[0]初始为true完全就是为了推导公式。

下标非0的dp[i]初始化为false，只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词。

4.确定遍历顺序
题目中说是拆分为一个或多个在字典中出现的单词，所以这是完全背包。

还要讨论两层for循环的前后循序。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

本题最终要求的是是否都出现过，所以对出现单词集合里的元素是组合还是排列，并不在意！

那么本题使用求排列的方式，还是求组合的方式都可以。

即：外层for循环遍历物品，内层for遍历背包 或者 外层for遍历背包，内层for循环遍历物品 都是可以的。

但本题还有特殊性，因为是要求子串，最好是遍历背包放在外循环，将遍历物品放在内循环。

如果要是外层for循环遍历物品，内层for遍历背包，就需要把所有的子串都预先放在一个容器里。（如果不理解的话，可以自己尝试这么写一写就理解了）

所以最终我选择的遍历顺序为：遍历背包放在外循环，将遍历物品放在内循环。内循环从前到后。

5.举例推导dp[i]
以输入: s = "leetcode", wordDict = ["leet", "code"]为例，dp状态如图：
（在下方）
dp[s.size()]就是最终结果。


ps:
五部曲中第一部是最困难的. 一般都是遵循"题目问什么, 就把`dp[]设置成什么


作者：carlsun-2
链接：https://leetcode.cn/problems/word-break/solution/dai-ma-sui-xiang-lu-139-dan-ci-chai-fen-50a1a/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

198 打家劫舍 medium

居然一开始和背包问题联系起来了，其实不是一回事啊！！

1
2
3
4
5
1.dp[i]表示考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]。
2.确定递推公式，决定dp[i]的因素就是第i房间偷还是不偷。偷第i间房子，那么dp[i] = dp[i-2]+nums[i]，因为不能导致报警，如果不偷第i间房子，dp[i]=dp[i-1]，这里不是表明要偷i-1房哦，要牢记dp[i]的概念，i以内的房间，所以dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
3.从递推公式可以看出，要初始化dp[0]和dp[1]，这里注意dp[1]是要求最大值哦，不是单纯赋值nums[1]
4.确定遍历顺序，从前到后
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int rob(int[] nums) {
        if (nums.length == 1) return nums[0];
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[1], nums[0]);
        for (int i = 2; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
        }
        return dp[nums.length - 1];

    }
}

213 打家劫舍2 medium

和上一题的区别是，上一题的房子都是在一条街道，而本题的房子，是围成一圈，第一间和最后一间挨着。

1
2
3
没做过的话，确实不好想
其实就是分成两部分，一部分不包含最后一个元素，一部分不包含第一个元素，然后比较他们的最大值
其余的和上一题一样。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int rob(int[] nums) {
        if (nums.length == 1) return nums[0];
        int end = nums.length - 1;
        return Math.max(robRange(nums, 0 , end - 1), robRange(nums, 1, end));

    }
    public int robRange(int[] nums, int start, int end) {
        if (start == end) return nums[start];//如果不写这句，遇到[0,0]会出错，因为这时候传进来的start和end都是相等的
        int[] dp = new int [nums.length];
        dp[start] = nums[start];//主体的逻辑也要根据start和end来写哦
        dp[start + 1] = Math.max(nums[start], nums[start + 1]);
        for (int i = start + 2; i <= end; i++) {//注意小于等于end
            dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);

        }
        return dp[end];//注意返回的是end
    }
}

337 打家劫设3 medium

这题用上了二叉树了，树形dp是第一次遇到！

1
2
3
4
5
6
7
首先要用后序遍历，因为通过递归函数的返回值来做下一步计算。

1.用长度为2的大小数组来保存，dp[0]表示不偷当前节点所获得的最大金钱，dp[1]表示偷当前节点所获得的最大金钱。
2.到了这里不是递推公式了，而是初始化，if (cur == NULL) return vector<int>{0, 0};，相当于初始化
3.确定遍历顺序，通过递归左节点，得到左节点偷与不偷的金钱。通过递归右节点，得到右节点偷与不偷的金钱。
4.确定单层递归的逻辑，如果是偷当前节点，那么左右孩子就不能偷，如果不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的，因为只要不挨着就行，所以不一定要偷的
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int rob(TreeNode root) {
        int[] res = dfs(root);
        return Math.max(res[0], res[1]);
    }
    public int[] dfs(TreeNode root) {
        int[] res = new int[2];//初始化
        if (root == null) {
            return res;
        }
        int[] left = dfs(root.left);//左孩子
        int[] right = dfs(root.right);//右孩子
        
        res[0] = Math.max(left[0],left[1]) + Math.max(right[0], right[1]);//不偷当前节点的话，左右孩子可以偷，也可以不偷，关键在于取最大
        res[1] = root.val + left[0] + right[0];//偷当前节点，那么左右孩子都不能偷，0代表不偷，left和right代表左右孩子
        return res;
    }
}

121 买卖股票的最佳时机 easy

只买卖一次！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
需要强化一个概念，持有不代表今天买，不持有不代表今天卖，可能是维持前一天的状态！！！！！



1.dp[i][0]代表第i天持有股票的最多现金，dp[i][1]代表第i天不持有股票股票所得最多现金，注意注意这里说的是“持有”，“持有”不代表就是当天“买入”！也有可能是昨天就买入了，今天保持持有的状态，也就是第二维的0和1代表持有和不持有，第一维只代表天
2.确定递推公式
第i天持有股票即dp[i][0]
持有表示可能之前就买了，那么就保持上一天的状态呗，也就是等于dp[i-1][0]
也可能表示今天买了，那么就是-price[i]
所以dp[i][0] = max(dp[i - 1][0], -prices[i]);

第i天不持有股票即dp[i][1]
不持有表示之前早就卖了，那就维持前一天的状态，dp[i-1][1]
也可能今天卖了，那就是dp[i-1][0]+prices[i],也就是前一天还是持有的状态，然后今天卖了，其实前一天的价格是负数，因为你持有了，加上今天的价格，就是利润
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);

3.从递推公式可以看到，需要依赖dp[0][0]和dp[0][1]
4.遍历顺序，从前往后
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
13
14
//动态规划
class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][2];
        dp[0][0] = -prices[0];//0代表持有
        dp[0][1] = 0; //1代表卖出，初始化不持有就表示现金为0
        for (int i = 1; i < prices.length; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return dp[prices.length - 1][1];//用第二个维度的1是因为，本题不持有股票状态所得金钱一定比持有股票状态得到的多！
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
//贪心算法，找最左最小值
class Solution {
    public int maxProfit(int[] prices) {
        int result = 0;
        int low =  Integer.MAX_VALUE;
        for (int i = 0; i < prices.length; i++) {
            low = Math.min(low, prices[i]);//找最左最小值
            result = Math.max(result, prices[i] - low);//取最大利润
        }
        return result;
    }
}

122 买卖股票的最佳时机2 medium

和上一题的区别是，这个题可以每天进行买卖，也就是可以多次买卖。最多只能持有一股股票，也可以先购买，然后在同一天出售。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][2];
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < prices.length; i++) {
            dp[i][0] = Math.max(dp[i - 1][1] - prices[i], dp[i - 1][0]);//唯一的区别，如果是第i天买入股票，所得现金就是昨天不持有股票的所得现金 减去 今天的股票价格
            dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);
        }
        return dp[prices.length - 1][1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
//贪心
class Solution {
    public int maxProfit(int[] prices) {
        int result = 0;
        for (int i = 1; i < prices.length; i++) {
            result += Math.max(prices[i] - prices[i - 1], 0);//把每次正利润都累加，所以这里用一个0来比较
        }
        return result;

    }
}

123 买卖股票最佳时机3 hard

限制了最多可以完成两笔交易！也就是买卖一次，可以买卖两次，也可以不买卖。这题难不少！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
这题和之前的状态不一样，之前的第二个维度，0代表持有，1代表不持有
1.确定下标含义

而本题只能最多买卖2次，那么可以设置5个状态，也是第二个维度来表示
0代表不操作
1代表第一次持有
2代表第一次不持有
3代表第二次持有
4代表第二次不持有

2.递推公式
以dp[i][1]为例
操作一：第i天买入股票了，那么dp[i][1] = dp[i-1][0] - prices[i]，注意这里是前一天的0
操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]
取他们最大

其他一样递推

3.
只需要初始化买入状态，即便第二次买入可能要考虑第一次买入
总之 dp[0][1],dp[0][3] = -price[0]
4.遍历顺序就是从左到右
5.推导

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int maxProfit(int[] prices) {
        //0没有操作，1第一次持有，2第一次不持有，3第二次持有，4第二次不持有
        int[][] dp = new int[prices.length][5];
        dp[0][1] = -prices[0];
        dp[0][3] = -prices[0];
        for (int i = 1; i < prices.length; i++) {
            dp[i][0] = dp[i - 1][0];//不写也能通过
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[prices.length - 1][4];
    }
}

188 买卖股票最佳时机4 hard

最多可以完成k笔交易，和上一题没啥区别，就是k次而已。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int maxProfit(int k, int[] prices) {
        if (prices.length == 0) return 0;//唯一区别，为了满足测试用例
        int[][] dp = new int[prices.length][2 * k + 1];
        for (int i = 1; i < 2 * k + 1; i = i + 2) {
            dp[0][i] = -prices[0];
        }
        for (int i = 1; i < prices.length; i++) {
            for (int j = 1; j < 2 * k + 1; j++) {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - 1] + (int)Math.pow(-1,j) * prices[i]);//注意int
            }
        }
        return dp[prices.length - 1][2 * k];
    }
}

309 最佳买卖股票时机含冷冻期 medium

比122多了一个冷冻期，支持多次交易，但是也不会太容易

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
关键在于有一个冷冻期，那么本题设置4种状态

1.持有（可能是保持前一天的持有状态，可能是今天买入）
2.不持有（这个不一样，反正今天不能卖！），两天前就卖出了股票，度过了冷冻期，一直没操作，今天保持卖出股票状态
3.卖出（也就是把之前股票问题的不持有状态拆成两个状态，一个不持有，一个卖出，等下讲解）
4.冷冻期，只有一天


2.递推公式

1.持有状态下
1.1 保持前一天的持有状态
1.2 昨天是冷冻期，今天买入
1.3 之前早就卖出股票并且度过了冷冻期，今天可以买入

2.不持有状态下
2.1 保持前一天的不持有的状态
2.2 冷冻期（这个不容易想到，因为冷冻期代表你已经卖了股票了，你可以保持这个状态表示不持有）

3.卖出
3.1 前一天持有了才能卖出

4.冷冻期
4.1 前一天卖出就会触发冷冻期

3.初始化
只需要设置持有状态下就可以，其他均为0，也就是dp[0][0] = -price[0]

4.遍历顺序就是从前到后
5.推导

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][4];
        dp[0][0] = -prices[0];
        for (int i = 1; i < prices.length; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], Math.max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][3]);
            dp[i][2] = dp[i - 1][0] + prices[i];
            dp[i][3] = dp[i - 1][2]; 

        }
        return Math.max(dp[prices.length - 1][1], Math.max(dp[prices.length - 1][2], dp[prices.length - 1][3]));
    }
}

714 买卖股票的最佳时机含手续费 medium

也是无限次交易，只是多了一个手续费，参考122就行啦，多一个手续费。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int maxProfit(int[] prices, int fee) {
        int[][] dp = new int[prices.length][2];
        dp[0][0] = -prices[0];
        for (int i = 1; i < prices.length; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
        }
        return dp[prices.length - 1][1];
    }
}

300 最长递增子序列 medium

1
2
3
4
5
6
7
8
1.dp[i]表示i之前包括i的以nums[i]结尾最长上升子序列的长度
2.位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。所以要用双重循环
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
这里注意j是大小是从0到i(不包含i)，我们需要取dp[j] + 1的最大值

3.初始化，这里和之前的dp问题有些不一样，每一个i的长度至少都是可以为1，所以全部先设置为1
4.顺序遍历
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        int result = dp[0];//不能设置为0
        for (int i = 1; i < nums.length; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                    result = Math.max(result, dp[i]);
                }
            }
        }
        return result;//本题不能直接用一维数组最后一个位置的值来返回，
    }
}

674 最长连续递增序列 easy

和上一题的区别是，本题要求连续，上一题的话可以隔开元素。

1
2
3
4
5
1.dp[i]：以下标i为结尾的数组的连续递增的子序列长度为dp[i]。
2.if (nums[i] > nums[i - 1]) dp[i] = Math.max(dp[i], dp[i - 1] + 1);因为要连续，所以需要比较上一个，而不是像上一题一样从0到j去找
3.初始化，也是全部初试化为1，因为每个i
4.确定遍历顺序，就是从前到后
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        int result = dp[0];//不能设置为0
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] > nums[i - 1]) {
                dp[i] = dp[i - 1] + 1;//注意没有max，要理解上题为什么有max
                result = Math.max(dp[i], result);
            }
        }
        return result;//本题不能直接用一维数组最后一个位置的值来返回，
    }
}

718 最长重复子数组 medium

也是连续子序列问题，但是这里是两个数组的对比

1
2
3
4
5
6
7
8
本题的含义不一样！！！注意看！！！本题的含义不一样！！！注意看！！！本题的含义不一样！！！注意看！！！

1.dp[i][j] ：以下标i-1为结尾的A（指第一个数组），和以下标j-1为结尾的B（指第二个数组），最长重复子数组长度为dp[i][j]。 （特别注意： “以下标i-1为结尾的A（指第一个数组）” 标明一定是 以A[i-1]为结尾的字符串 ）
以前都是下标i，但是本题是下标i-1，我是这么觉得的，因为比较的时候，从0开始的话，往前面推是-1，因为这里涉及两个数组，不方便，而且我们回过头去看之前的dp问题，也是有i-1的元素在的，而本题是同时比较两个数组
2.当A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1;
3.初始化，0即可，dp[i][0] 和dp[0][j]初始化为0，java的话本来就默认0
4.循环遍历，从前到后，第一组先，然后再第二组
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];//注意两个数组可能大小是不一样的！！！！
        int result = dp[0][0];//方便在遍历的时候就找到最大值
        for (int i = 1; i <= nums1.length; i++) {
            for (int j = 1; j <= nums2.length; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;//没有max比较
                    result = Math.max(result, dp[i][j]);
                }
            }
        }
        return result;//本题不能直接用二维数组最后一个位置的值来返回
    }
}

1143 最长公共子序列 medium

连续的

1
2
3
4
5
6
7
8
9
10
11
12
1.dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列长度为 dp[i][j]
2.确定递推公式
text1[i-1] 与 text2[j-1]相同情况下
如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

text1[i-1] 与 text2[j-1]不相同情况下(重点理解这里，不是太好理解)
如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

3.统一初始化为0
4.从前到后遍历
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int[][] dp = new int[text1.length() + 1][text2.length() + 1];
        int result = dp[0][0];
        for (int i = 1; i <= text1.length(); i++) {
            for (int j = 1; j <= text2.length(); j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);//这个不容易理解
                }
                result =Math.max(dp[i][j], result);

            }
        }
        return result;//其实本题是可以直接返回dp[text1.length()][text2.length()]，不需要result也可以。
    }
}

最长序列问题总结

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
总体分为几种情况的组合，单数组和双数组，连续或者子序
1.定义
如果是单数组，就直接定义一维的，直接按照0~i-1的位置来即可，定义长度就是数组长度，但是如果是双数组，用i-1代表dp[i][j]更好，也就是长度需要加1，同时双数组就定义两个维度。
2.状态转移方程需要根据题目意思来
3.确定初始化，对于单数组，都是比较自己，因为单独一个元素就是一个长度序列，所以应该全部初始化为1，但是对于双数组，则需要比较，所以在比较的情况下再确定长度，也就是初始化为0即可。
4.从前到后遍历
5.推导数组

另外说几点，对于求连续的，不需要max来比较，直接前一个位置+1就行
但是对于子序，需要考虑前面的所有情况

另外说下关于返回值的问题，以前我们的dp问题，都能用数组的最后一个位置的值返回，但是本系列只有1143可以这么做
我的理解是这样的，最重要是看dp的定义
300：i之前包括i的以nums[i]结尾最长上升子序列的长度，以他为结尾，意味着他要包含进去，但是包含他的，不一定是最长的长度，所以要不断找最大值
674：以下标i为结尾的数组的连续递增的子序列长度为dp[i]，也是和上面一样的意思去判断
718：以下标i-1为结尾的A，和以下标j-1为结尾的B，最长重复子数组长度为dp[i][j]，也是和上面一样
所以上面三个题，都需要来比较来找到最大值
1143：长度为[0,i-1]的字符串text1与长度为[0,j-1]的字符串text2的最长公共子序列长度为dp[i][j]

当然了，其实我是在知道定义后写的，至于1143为什么不是以结尾来定义，还没弄明白，如果觉得不好记，统一用max比较也可以

1035 不相交的线 medium

需要拆解为，两个字符串的最长公共子序列的长度！也就是和上一题一毛一样！ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];
        int result = dp[0][0];
        for (int i = 1; i <= nums1.length; i++) {
            for (int j = 1; j <= nums2.length; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
                result = Math.max(result, dp[i][j]);
            }
        }
        return result;
    }
}

53 最大子数组和 medium

这个题是连续部分，不是子序，这个题一开始还有点懵，需要理解一下。

1
2
3
4
5
1.dp[i]：包括下标i之前的最大连续子序列和为dp[i]。
2.两个方向来推：2.1 dp[i-1]+nums[i]，即：nums[i] 2.2加入当前连续子序列和nums[i]，即：从头开始计算当前连续子序列和
3.初始化为0
4.从前到后遍历
5.推导
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        int sum = nums[0];
        dp[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
            sum = Math.max(sum, dp[i]);
        }
        return sum;
    }
}

392 判断子序列 medium

和1143,1035差不多，但是本题注意是s是否t的子序列，也就是最长子序列长度必须要为s的长度才可以。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public boolean isSubsequence(String s, String t) {
        int[][] dp = new int[s.length() + 1][t.length() + 1];
        int max = dp[0][0];
        for (int i = 1; i <= s.length(); i++) {
            for (int j = 1; j <= t.length(); j++) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
                max = Math.max(max, dp[i][j]);
            }
        }
        return max == s.length();
    }
}

115 不同的子序列 hard

这个题真的超级难懂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
1143是找最长公共子序列
而本题是字符串s有很多个子序列(不一定连续)，这些子序列字符串中，字符串t出现了多少次？
也就是计算在 s 的子序列中 t 出现的个数。


1.dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
2.递推顺序（https://leetcode.cn/problems/distinct-subsequences/solution/tu-jie-dong-tai-gui-hua-by-cyingenohalt-nnlc/）
第一种情况s[i-1]与t[j-1]不相等
第一种解释：我们发现当sub_s新增了一个长度后，如果新增的字符（当前sub_s尾字符），与sub_t尾字符不匹配，那么似乎在sub_s上多了个"没用"的字符，sub_s所有子序列字符串中sub_t出现的次数没有任何变化。因此在这种状态下：dp[i][j]=dp[i-1][j];
第二种解释：s[i−1]不能和t[j−1] 匹配，因此只考虑t[j-1]作为s[i-2]的子序列，子序列个数为dp[i-1][j]dp[i−1][j]

第二种情况：s[i-1]与t[j-1]相等
第一种解释：如果新加入sub_s的这个字符与sub_t尾字符相匹配时，在没有增加这个字符的情况下，sub_t出现的次数是dp[i-1][j], 现在增加了并且和sub_t尾字符相匹配，因此还要在这个基础上加上两者此前的状态下的次数，即dp[i-1][j-1]，因为相比此前，两者都多了同一个字符，与两者没有加上这个相同字符时情况是一样的。因此这种情况下总和是dp[i-1][j]+dp[i-1][j-1]

3.初始化
如果 j=0 即 t[j]为空字符串，由于空字符串是任何字符串的子序列，因此对任意dp[i][0]=1；
如果 i=0即 s[i]为空字符串，t[j]为非空字符串，由于非空字符串不是空字符串的子序列，因此 dp[0][j]=0。//这个java默认，可以不用管
4.从前到后遍历，从1开始
5.推导数组


这个题为什么没有加1操作，因为这个题是求出现的次数，如果你下一个字符是相等的，那么他们的出现次数是和之前一样的（我自己理解，不一定对）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int numDistinct(String s, String t) {
        int[][] dp = new int[s.length() + 1][t.length() + 1];
        for (int i = 0; i <= s.length(); i++) {
            dp[i][0] = 1;
        }
        for (int i = 1; i <= s.length(); i++) {
            for (int j = 1; j <= t.length(); j++) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[s.length()][t.length()];
    }
}

583 两个字符串的删除操作 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
和上一题的区别是，本题可以任意删除其中一个字符串
1.dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数。
2.确定递推公式
情况1：当word1[i-1]与word2[j-1]相同的时候
可以理解为，相同，所以不用删，那就复用上一次的结果
dp[i][j]=dp[i-1][j-1];

情况2：当word1[i-1]与word2[j-1]不相同的时候，有三种情况
删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1
删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1
同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2，因为每操作一次，就要加一，这里同时各操作了一次
dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});

3.初始化
dp[i][0]：word2为空字符串，以i-1为结尾的字符串word1要删除多少个元素，才能和word2相同呢，很明显dp[i][0] = i。
dp[0][i]：word1为空字符串，以i-1为结尾的字符串word2要删除多少个元素，才能和word1相同呢，很明显dp[0][i] = i。

4.从前到后遍历
5.推导数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int minDistance(String word1, String word2) {
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];
        for (int i = 0; i <= word1.length(); i++) {
            dp[i][0] = i;
        }
        for (int i = 0; i <= word2.length(); i++) {
            dp[0][i] = i;
        }  
        for (int i = 1; i <= word1.length(); i++) {
            for (int j = 1; j <= word2.length(); j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(dp[i - 1][j - 1] + 2, Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
                }
            }
        }      
        return dp[word1.length()][word2.length()];
    }
}

72 编辑距离 hard

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
上一题是任何一个字符串都能删除，本题的话，可以进行删，改，增，或者不操作
我看题解的时候，官方表达的意思是两个字符都能操作，但是实际题目意思，我感觉是只能操作1，然后让其变成2

1.dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。
2.确定递推公式，分为两个情况
情况1：word1[i-1] == word2[j-1]
dp[i][j] = dp[i - 1][j] + 1

情况2：word1[i-1] != word2[j-1]

操作1：word1删除一个元素//word1的[0,i-1]位置与word2的[0,j]位置的字符已匹配, 加1代表执行word1[i]的删除操作
dp[i][j] = dp[i-1][j] + 1
操作2：word2删除一个元素（相当于word1的插入操作）
dp[i][j] = dp[i][j-1]+1//word1的[0,i]位置与word2的[0,j-1]位置的字符已匹配, 加1代表执行word1[i]的插入操作
操作3：word1替换操作
dp[i][j] = dp[i-1][j-1]+1//word1的[0,i-1]位置与word2的[0,j-1]位置的字符已匹配, 加1代表执行word1[i]->word2[j]的替换操作
然后取他们的最小值，即
dp[i][j] = min({dp[i-1][j-1], dp[i-1][j], dp[i][j-1]}) + 1;

3.初始化dp
和上一题一样
dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i;
dp[0][i]就应该是i，对word2里的元素全部做删除操作，即：dp[0][i] = i;

4.遍历顺序
从前到后
5.推导公式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int minDistance(String word1, String word2) {
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];
        for (int i = 0; i <= word1.length(); i++) {
            dp[i][0] = i;
        } 
        for (int i = 0; i <= word2.length(); i++) {
            dp[0][i] = i;
        }
        for (int i = 1; i <= word1.length(); i++) {
            for (int j = 1; j <= word2.length(); j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
                }
            }
        }
        return dp[word1.length()][word2.length()];        
    }
}

647 回文子串 medium

本题遍历顺序不一样，注意看！！！本题是连续的字符串，而且是算个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
注意本题的dp数组是布尔类型   

1.布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false
2.确定递推公式
分为两种情况
情况1：s[i]与s[j]相等
2.1下标i与j相同，同一个字符例如a，是回文子串
2.2下标i与j相差为1，例如aa，也是回文子串
2.3i与j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是i+1与j-1区间，这个区间是不是回文就看dp[i+1][j-1]是否为true

情况1：s[i]与s[j]不相等
直接为false

3.初始化dp
一开始当然都是false啦，都没有匹配上
4.遍历顺序，不是按顺序，不是按顺序，不是按顺序！！！！
我们可以看到2.3这情况，根据dp[i + 1][j - 1]是否为true，在对dp[i][j]进行赋值true的，然后dp[i + 1][j - 1]在dp[i][j]左下角，也就是遍历顺序是下到上，左到右，可以理解为从斜左下角推导到右上角。
5.推导数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int countSubstrings(String s) {
        boolean[][] dp = new boolean[s.length()][s.length()];
        int result = 0;
        for (int i = s.length() - 1; i >= 0 ; i--) {//从下到上遍历
            for (int j = i; j < s.length(); j++) {//注意j不是从0开始，然后从左到右
                if (s.charAt(i) == s.charAt(j) && (j - i <= 1 || dp[i + 1][j - 1])) {//j - i <= 1包含2.1和2.2情况，dp[i + 1][j - 1]也就是2.3情况
                    result++;
                    dp[i][j] = true;
                }
             }    
         }
    return result;
    }
}

516 最长回文子序列 medium

注意本题是求子序的最长长度

1
2
3
4
5
6
7
8
9
10
1.dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
2.确定递推公式
s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;//因为长度加2，注意里面是i+1和j-1的基础上，是字串的基础上加2
s[i]与s[j]不相同（可以看卡哥的图），说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。加入s[i]的回文子序列长度为dp[i][j - 1]。那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
3.初始化dp
首先要理解定义，所以i和j相等，那长度肯定是1的，因为他们就是指示一个字符
dp[i][i] = 1;
4.遍历顺序，和上面一题一样，也是从左下角到右上角，也就是从下到上，从左到右
5.推导数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int longestPalindromeSubseq(String s) {
        int[][] dp = new int[s.length()][s.length()];
        for (int i = 0; i < s.length(); i++) {
            dp[i][i] = 1;
        }
        int result = dp[0][0];
        for (int i = s.length() - 1; i >= 0; i--) {
            for (int j = i + 1; j < s.length(); j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
                }
                result = Math.max(result, dp[i][j]);
            }
        }
        return result;//return dp[0][s.length() - 1];也可以但是不好记
    }
}

单调栈

1
2
如果找更大的元素，需要构建单调递减栈
如果找更小的元素，需要构建单调递增栈

739 每日温度 medium

1
2
3
4
5
6
7
8
9
10
11
12
//单调栈方法,通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了
分为三种情况
栈里面是存储数组的下标，而不是值
1.当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
把T[i]的下标入栈

2.当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
把T[i]的下标入栈

3.当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
计算距离放入result中，将栈顶元素弹出。
等到不符合条件了（也就是栈里面的元素下标已经大于当前T[i]），那么这时候就把T[i]入栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//在LinkedList中，poll方法是检测并删除头元素，peek是单纯检索头元素（类似于栈，头元素就是最后加进去的那个元素）
class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int[] result = new int[temperatures.length];
        Deque<Integer> stack = new LinkedList<>();
        stack.push(0);
        for (int i = 1; i < temperatures.length; i++) {
            if (temperatures[i] <= temperatures[stack.peek()]) {
                stack.push(i);//合并情况1和2
            } else {
                while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {//情况3，注意栈不能为空
                    result[stack.peek()] =  i - stack.peek();
                    stack.pop();
                }
                stack.push(i);
            }
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//暴力循环，找到第一个大的就break，但是复杂度很高
class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int[] result = new int[temperatures.length];
        for (int i = 0; i < temperatures.length; i++) {
            for (int j = i + 1; j < temperatures.length; j++) {
                if (temperatures[j] > temperatures[i]) {
                    result[i] = j - i;
                    break;
                }
            }
        }
        return result;
    }
}

496 下一个更大元素1 easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//单调栈，和上一题的思路是差不多的，关键在于，这里是两个数组

首先我们用一个map把数组1的<数值，下标>存进去

然后操作数组2，数组2的操作逻辑也是
1.当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
把T[i]的下标入栈

2.当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
把T[i]的下标入栈

3.当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
这时候可以找到右边第一个比自己大的元素
判断栈顶元素是否在nums1里出现过，（注意栈里的元素是nums2的元素），如果出现过，开始记录结果。
然后出栈

当不满足大于栈顶元素，就把当前元素入栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        Deque<Integer> stack = new LinkedList<>();
        int[] result = new int[nums1.length];
        Arrays.fill(result, -1);
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums1.length; i++) {
            map.put(nums1[i], i);
        }
        stack.push(0);
        for (int i = 1; i < nums2.length; i++) {
            if (nums2[i] <= nums2[stack.peek()]) {
                stack.push(i);
            } else {
                while (!stack.isEmpty() && nums2[i] > nums2[stack.peek()]) {
                    if (map.containsKey(nums2[stack.peek()])) {
                        Integer index = map.get(nums2[stack.peek()]);
                        result[index] = nums2[i];
                    }
                    stack.pop();
                }
                stack.push(i);
            }
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//暴力出奇迹
class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        int[] result = new int[nums1.length];
        Arrays.fill(result, -1);
        for (int i = 0; i < nums1.length; i++) {
            for (int j = 0; j < nums2.length; j++) {
                if (nums1[i] == nums2[j]) {
                    for (int x = j + 1; x < nums2.length;x++) {
                        if (nums2[x] > nums1[i]) {
                            result[i] = nums2[x];
                            break;
                        }
                    }
                }
            }
        }
        return result;
    }
}

503 下一个更大元素2 medium

本题关键在于 如何处理循环数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//处理循环数组，太秒了，循环的时候，把数组变成两倍的长度，然后用%可以走两遍数组
class Solution {
    public int[] nextGreaterElements(int[] nums) {
        int[] result = new int[nums.length];
        Deque<Integer> stack = new LinkedList<>();
        Arrays.fill(result, -1);
        stack.push(0);
        for (int i = 1; i < 2 * nums.length; i++) {
            if (nums[i % nums.length] <= nums[stack.peek()]) {
                stack.push(i % nums.length);
            } else {
                while (!stack.isEmpty() && nums[i % nums.length] > nums[stack.peek()]) {
                    result[stack.peek()] = nums[i % nums.length];//或者用poll，那么pop就省略了
                    stack.pop();
                }
                stack.push(i % nums.length);
            }
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//暴力出奇迹，找完右边再重新找左边
class Solution {
    public int[] nextGreaterElements(int[] nums) {
        int[] result = new int[nums.length];
        Arrays.fill(result, -1);
        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[j] > nums[i]) {
                    result[i] = nums[j];
                    break;
                }
                for (int x = 0; x < i; x++) {
                    if (nums[x] > nums[i]) {
                        result[i] = nums[x];
                        break;
                    }
                } 
            }
        }
        for (int i = 0; i < nums.length - 1; i++) {
            if (nums[i] > nums[nums.length - 1]) {
                result[nums.length - 1] = nums[i];
                break;
            }
        }
        return result;
    }
}

42 接雨水 hard

高频率题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
单调栈做法
单调递减栈

注意用单调栈的做法计算面积和双指针略有不同,双指针直接就是先找到最左边最高，最右边最高，然后用他们比较小的那个减去当前高度就是体积（因为当前高度的宽是1，不用长*宽了）

栈：先进去的是栈底，
当前元素小于等于栈顶元素，那么就入栈

如果大于了栈顶元素，这时候就可以找出三个元素
right下标就是当前i小标
mid就是栈顶下标，用了之后要取出来，为什么要取出来，因为用过了。
left就是下一个栈顶下标，这里不用取出来，因为下一次还要用
h是高度，右边下标的对应的值（是指，不是下标数）和左边小标对应的值找到较小那个-当前i的高度
w是宽度，用右边下标-左边下标-1（-1是因为算两个栈中间的区域长度，0 1 2 3，比如0和3，中间的长度就是2,3-0-1=2）
然后h*w即可
这里为什么和双指针那个算法不一样，其实我认为是因为单调栈这样出栈顺序，不是他的左边最高和右边最高，这样出栈是单纯能算出体积
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int trap(int[] height) {
        int sum = 0;
        Deque<Integer> stack = new LinkedList<>();
        stack.push(0);
        for (int i = 1; i < height.length; i++) {
            if (height[i] <= height[stack.peek()]) {
                stack.push(i);
            } else {
                while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
                    int mid = stack.poll();//拿到后要取出
                    if (!stack.isEmpty()) {//注意这里，有点不一样，还需要判断一次
                        int right = i;
                        int left = stack.peek();
                        int h = Math.min(height[right], height[left]) - height[mid];
                        int w = right - left - 1;
                        sum += h * w;
                    }
                }
                stack.push(i);
            }
        }
        return sum;
    }
}
1
2
3
4
5
6
7
8
9
本题用双指针解法（但是力扣官方是写暴力解法），这个比较容易懂

首先清楚，第一根柱子和最后一根柱子，是不接雨水的，所以遍历的时候跳过这两个

然后要清楚，雨水是如何计算的
对于每一列，我们都要找出他左边最高的一个柱子（包含第一格），同时找出右边最高的柱子（包含最后一格）
然后选出他们两个高度之间小的那个，减去本列的高度，就是雨水的体积，因为长度都是1，所以1*高度就是雨水体积

那么我们只要找到每一格的高度，就可以完成任务
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int trap(int[] height) {
        int sum = 0;
        for (int i = 1; i < height.length - 1; i++) {//第一格和最后一格不算

            int lheight = height[i];
            int rheight = height[i];

            for (int l = 0; l < i; l++) {//找到本列左边最高的柱子，包含第一格
                if (height[l] > lheight) lheight = height[l];
            }

            for (int r = i + 1; r < height.length; r++) {//找到本列右边最高的柱子，包含最后一格
                if (height[r] > rheight) rheight = height[r];
            }
            int high = Math.min(lheight, rheight) - height[i];//雨水取决于短板

            if (high > 0) sum += high;//其实不用high大于0也是可以的
        }
        return sum;
    }
}

84 柱状图中最大的矩形 hard

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
找每个柱子左右侧的第一个高度值小于该柱子的柱子，注意和上一题的区别

单调栈：栈顶到栈底：从大到小（每插入一个新的小数值时，都要弹出先前的大数值）
栈顶，栈顶的下一个元素，即将入栈的元素：这三个元素组成了最大面积的高度和宽度
情况一：当前遍历的元素heights[i]大于栈顶元素的情况
情况二：当前遍历的元素heights[i]等于栈顶元素的情况
情况三：当前遍历的元素heights[i]小于栈顶元素的情况

这里是找到左右侧高度小于当前的，所以用单调递增栈

当前高度大于等于栈顶，入栈
当前高度小于栈顶

mid高度栈顶下标，用了需要取出来
right就是当前元素下标
left就是栈顶下标（之前取出了一个mid，这个是新栈顶）

面积就是 (right-left-1)*mid
减去1可以继续看下面的图理解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int largestRectangleArea(int[] heights) {
        int[] newheights = new int[heights.length + 2];
        int result = 0;
        for (int i = 0; i < heights.length; i++) {
            newheights[i + 1] = heights[i];
        }
        heights = newheights;
        Deque<Integer> stack = new LinkedList<>();
        stack.push(0);
        for (int i = 1; i < heights.length; i++) {
            if (heights[i] >= heights[stack.peek()]) {
                stack.push(i);//情况1和2
            } else {
                while (!stack.isEmpty() && heights[i] < heights[stack.peek()]) {
                    int mid = heights[stack.poll()];
                    int right = i;
                    int left = stack.peek();
                    int width = right - left - 1;
                    result = Math.max(result, width * mid);
                }
                stack.push(i);
            }
        }
        return result;

    }
}

借用别人画的图来理解如何计算面积
比如计算5（下标是2）的最大面积
左边小的是1（下标1），右边小的是2（下标4）
面积就是（4-1-1）* 5=10

比如计算6（下标是3）的最大面积
左边小的是5（下标2），右边小的是2（下标4）
面积就是（4-2-1）* 6=6

hot100

3 无重复字符的最长子串

1
2
3
4
5
用一个map来保存字符
双指针的做法
一个start 一个end
如果发现重复了（map中），需要重新找到start的位置，新start的位置需要这个字符在map的位置然后加1，但是start不能往回走（因为单纯加1的话，可能会回退，因为字符可能在最开始的位置），所以要在start和 这个字符在map的数字加1比较，确定新start的位置
长度就是end-start+1,在过程中记录即可，然后把字符加入到map中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int lengthOfLongestSubstring(String s) {
        int n = s.length(), ans = 0;
        Map<Character, Integer> map = new HashMap<>();
        for (int end = 0, start = 0; end < n; end++) {
            char alpha = s.charAt(end);
            
            if (map.containsKey(alpha)) {
                start = Math.max(map.get(alpha) + 1, start);
            }

            ans = Math.max(ans, end - start + 1);
            map.put(s.charAt(end), end);
        }
        return ans;
    }
}

5 最长回文子串 medium

思路挺简单的，仔细阅读下代码，用的是暴力法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public String longestPalindrome(String s) {
        int len = 1;
        int begin = 0;
        for (int i = 0; i < s.length(); i++) {
            for (int j = i + 1; j < s.length(); j++) {
                if (j - i + 1 > len && valid(s, i, j)) {//注意这里是把整个s带进去
                    len = j-i+1;
                    begin = i;
                }
            }
        }
        return s.substring(begin, begin + len);
    }
    public boolean valid(String s, int start, int end) {       
        for (int i = start, j = end; i < j; i++,j--) {
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
        }
        return true;   
    }
}

11 盛水最多的容器 medium

需要和42 84一起看

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/*
本题的思路是用双指针，一个最左边，一个最右边
每次都是固定长的那根，然后计算面积（较短的那根*距离）
然后每次移动比较短的那根
*/
class Solution {
    public int maxArea(int[] height) {
        int result = 0;
        for (int i = 0; i < height.length; i++) {
            for (int j = i + 1; j < height.length; j++) {
                int high = Math.min(height[i], height[j]);
                int width = j - i;
                result = Math.max(result, high * width);
            }
        }
        return result;
    }
}

128 最长连续序列 medium

注意这个题，是指内部可以组成的连续的序列，比如1,2,3,4,5，累加1这种，但是，不是指必须他们在位置上连续，他们一开始是打乱的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/*
用set，因为数组是可能中间有连续一样的数字，set可以用来保留一个
*/
class Solution {
    public int longestConsecutive(int[] nums) {
        HashSet<Integer> set = new HashSet<>();
        for (int x : nums) {
            set.add(x);
        }
        int result = 0;
        int temp = 0;
        for (int i : nums) {
            if (!set.contains(i - 1)) {//只有当num-1不存在时，才开始向后遍历，如果没有这句话，会超时的
                while (set.contains(i)) {
                    temp++;
                    i++;//在这里进行++，因为连续嘛，比前一个数大于1就可以连续
                }
                result = Math.max(result, temp);
            }
            temp = 0;
        }
        return result;
    }
}

146 LRU缓存 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
LinkedHashMap是尾插

LinkedHashMap和HashMap不一样，HashMap是无序的，前者是有序的，所以不能用hashmap来做这个题
1.查询操作
存在的话，先对他进行最近操作处理，然后返回值
否则返回-1

2.插入操作
如果这个key本身存在的话，先对他进行最近操作处理，然后把value更新，并且中断操作
如果key不存在，先判断插入的时候，是否满了，先删除头部的老节点，然后再插入

最近操作处理
先存这个value，然后删除key，然后再重新put即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class LRUCache {
    int capacity;
    LinkedHashMap<Integer, Integer> cache = new LinkedHashMap<>();

    public LRUCache(int capacity) {
        this.capacity = capacity;
    }
    
    public int get(int key) {
        if (cache.containsKey(key)) {
            makeRecently(key);
            return cache.get(key);
        }
        return -1;
    }
    
    public void put(int key, int value) {
        if (cache.containsKey(key)) {
            makeRecently(key);
            cache.put(key, value);
            return;//这个很重要，不然不能通过，否则会往下走
        }
        if (cache.size() == this.capacity) {
            int oldKey = cache.keySet().iterator().next();//学习这个写法
            cache.remove(oldKey);
        }
        cache.put(key, value);

    }

    private void makeRecently(int key) {
        int value = cache.get(key);
        cache.remove(key);
        cache.put(key, value);

    }
}

152 乘积最大子数组 medium

对比53题

1
2
3
4
5
6
7
这题最大的不同点在于需要维护两个dp数组，一个最大的，一个最小的
一般我们都是维护一个最大的即可，这里说下如果不维护一个最小的
比如[-2,3,-4]
dp[0] = -2
dp[1] = 3
dp[2] = 3
但是，其实正确答案是24，因为可能中间是负数，后面是负数，就可以变成正数，但是单纯用max的话，会忽略掉中间负数的情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int maxProduct(int[] nums) {
        int[] dpmax = new int[nums.length];
        int[] dpmin = new int[nums.length];
        //Arrays.fill(dp, 1);
        dpmax[0] = nums[0];
        dpmin[0] = nums[0];
        int result = nums[0];
        for (int i = 1; i < nums.length; i++) {
            dpmax[i] = Math.max(Math.max(nums[i] * dpmax[i - 1], nums[i] * dpmin[i - 1]), nums[i]);
            dpmin[i] = Math.min(Math.min(nums[i] * dpmax[i - 1], nums[i] * dpmin[i - 1]), nums[i]);
            result = Math.max(result, dpmax[i]);
        }
        return result;
    }
}

136 只出现一次的数字 easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/*
异或运算
十进制下相同数字异或结果为0，数字a与0异或结果仍为原来的数字a。
还有就是异或运算支持结合律，所以你的数组顺序是无所谓的
计算完后剩下的就是出现那一个的数
*/
class Solution {
    public int singleNumber(int[] nums) {
        int single = 0;
        for (int num : nums) {
            single ^= num;
        }
        return single;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//这个不符合题目不用额外空间的要求，但是能pass
class Solution {
    public int singleNumber(int[] nums) {
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i : nums) {
            map.put(i, map.getOrDefault(i, 0) + 1);
        }
        for (int i : nums) {
            if (map.get(i) == 1) {
                return i;
            }
        }
        return 0;

    }
}

283 移动零 easy

注意题目要在原数组上操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/*
左指针指向当前已经处理好的序列的尾部，右指针指向待处理序列的头部。
其实第一次看这个做法，还挺奇妙的，只用了一次遍历
可以理解为，left会指向下一个0，然后等着right找到不是0，进行交换
*/
class Solution {
    public void moveZeroes(int[] nums) {
        int left = 0;
        for (int right = 0; right < nums.length; right++) {
            if (nums[right] != 0) {////当前元素!=0，就把其交换到左边，等于0的会交换到右边
                swap(nums, left, right);
                left++;
            }
        }
    }
    public void swap(int[] nums, int left, int right) {
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp; 
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//这种是补0，好像和意思不太对，但是也能做
class Solution {
    public void moveZeroes(int[] nums) {
        int slow = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0) {
                nums[slow] = nums[i];
                slow++;
            }
        }
        for (int j = slow; j < nums.length; j++) {
            nums[j] = 0;
        }
    }
}

169 多数元素 easy

统计次数，用map

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int majorityElement(int[] nums) {
        int result = nums[0];
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i : nums) {
            map.put(i, map.getOrDefault(i, 0) + 1);
            if (map.get(i) > nums.length / 2) {
                result = i;
            }
        }
        return result;
    }
}

234 回文链表 easy

自己写的，看

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public boolean isPalindrome(ListNode head) {
        StringBuilder s = new StringBuilder();
        ListNode cur = head;
        while (cur != null) {
            s.append(cur.val);
            cur = cur.next;
        }
        String a = s.toString();
        int j = a.length() - 1;
        for (int i = 0; i < a.length(); i++) {
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
            j--;
        }
        return true;
    }
}

448 找到所有数组中消失的数字 easy

用set来保存数，然后遍历1~n，看看哪个数不在就添加

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer> list = new LinkedList<>();
        Set<Integer> set = new HashSet<>();
        for (int i : nums) {
            set.add(i);
        }
    
        for (int i = 0; i < nums.length; i++) {
            if (!set.contains(i + 1)) {
                list.add(i + 1);
            }
        }
        return list;
    }
}

287 寻找重复数 medium

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//不过不满足题目的要求
class Solution {
    public int findDuplicate(int[] nums) {
        HashMap<Integer, Integer> map = new HashMap<>();
        int result = nums[0];

        for (int i : nums) {
            map.put(i, map.getOrDefault(i, 0) + 1);
            if (map.get(i) > 1) {
                result = i;
            }
        }
        return result;

    }
}

560 和为 K 的子数组 medium

1
2
这个解法很少见，先找到每个下标，然后从这个下标开始倒着加，如果中途满足k，就计数
当然顺着加也可以（注释中的语句），即先固定左边界，然后枚举右边界哈，
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0;
        for (int start = 0; start < nums.length; start++) {
            int sum = 0;
            for (int end = start; end >= 0; end--) {//for (int end = start; end < nums.length; end++)也可以，这个我觉得更好理解，倒着来太麻烦   
                sum += nums[end];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
}

前缀和解法，前缀和就是前i个数的和，left和right区间内的前缀和相减如果等于k，就说明中间有连续数组是为k

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int subarraySum(int[] nums, int k) {
        int[] presum = new int[nums.length + 1];
        presum[0] = 0;//注意第一个不算，置为0
        for (int i = 0; i < nums.length; i++) {
            presum[i + 1] = presum[i] + nums[i];
        }
        int count = 0;
        for (int i = 0; i <= nums.length; i++) {
            for (int j = i + 1 ; j <= nums.length; j++) {
                if (presum[j] - presum[i] == k) {
                    count++;
                }
            }
        }
        return count;
    }
}

581 最短无序连续子数组 medium

1
2
3
其实就是新建一个拍好序的数组，然后从左边遍历看第一个不正确的数，记录left
然后从右边遍历第一个不正确的数，记录right。这里需要注意，不能用sortnum = num，因为这样操作是浅拷贝，如果你把sortnum排序了，那么num也会变的！！！！
比如[2,6,4,8,10,9,15]，最终记录left为1，right为5，然后务必+1才是长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int left = 0;
        int right = nums.length - 1;
        int sortnum[] = new int[nums.length];
        for (int i = 0; i < nums.length; i++) {
            sortnum[i] = nums[i];
        }


        Arrays.sort(sortnum);
        while (left < nums.length && nums[left] == sortnum[left]) {
            left++;
        }
        while (right > 0 && nums[right] == sortnum[right]) {
            right--;
        }

        if (right == 0){
            return 0;
        }

                 
        return right - left + 1;
    }
}

461 汉明距离 easy

单纯计算二进制，然后比较

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int hammingDistance(int x, int y) {
        int result = 0;
        while (x != 0 || y != 0) {
            if (x % 2 != y % 2) {
                result++;
            }
            x = x / 2;
            y = y / 2;
        }
        return result;
    }
}

2 两数相加 medium

1
2
3
4
5
这个题的关键是遇到两位数的和，需要把十位上的数，累加到下一次中，举个例子
[2,4,3]
[5,6,7]
他们的和是7,10,10，第二个数已经超过了10，把0保留，1留在下一个中，就是7,0,11，然后11又超过了两位数，所以把1留下，最后是7,0,1,1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode dump = new ListNode(-1);
        ListNode cur = dump;
        //ListNode pre = dump;
        int carry = 0;
        while (l1 != null || l2 != null) {
            int x = l1 == null ? 0 : l1.val;
            int y = l2 == null ? 0 : l2.val;
            int sum = x + y + carry;
            carry = sum / 10;
            sum = sum % 10;
            cur.next = new ListNode(sum);//这里前面不需要再声明ListNode
            cur = cur.next;
            if (l1 != null) {
                l1 = l1.next;
            }
            if (l2 != null) {
                l2 = l2.next;
            }
        }
        if (carry == 1) {//处理最后遗留的carry，因为最大也就是相加之和为18，所以只能是1
            cur.next = new ListNode(1);
        }
        return dump.next;
    }
}

338 比特位计数 easy

很简单，计算二进制即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int[] countBits(int n) {
        int[] result = new int[n + 1];
        for(int i = 0 ; i <= n; i++) {
            result[i] = count(i);
        }
        return result;
    }
    public int count(int x) {
        int sum = 0;
        while (x != 0) {//注意条件是x != 0
            if (x % 2 == 1) {
                sum++;
            }
            x = x / 2;
        }
        return sum;
    }

23 合并K个升序链表 hard

思想参考21题，放在本题就是合并两两链表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        ListNode dump = null;
        for (int i = 0; i < lists.length; i++) {
            dump = mergetwoLists(dump, lists[i]); 
        }
        return dump;   
    }
    public ListNode mergetwoLists(ListNode list1, ListNode list2) {
        //这个可要可不要
        /*  
        if (list1 == null || list2 == null) {
            return list1 == null ? list2 : list1;
        }
        */
        ListNode dump = new ListNode(-1);
        ListNode cur = dump;
        while (list1 != null && list2 != null) {
            if (list1.val < list2.val) {
                cur.next = list1;
                list1 = list1.next;
            } else {
                cur.next = list2;
                list2 = list2.next;
            }
            cur = cur.next;
        }
        cur.next = list1 == null ? list2 : list1;
        return dump.next; 
    }
}

238 除自身以外数组的乘积 medium

1
2
3
4
5
6
7
8
9
10
11
先算左侧数字累积，也就是当前元素之前元素的累积（不含当前元素）
然后倒过来算累计，也就是当前元素之后元素的累积，在左侧数字累积的基础上相乘，这样就可以算出除自身外的累积
总体思想也就是左侧数字的累积乘以右侧数字的累积，也就是除了这个数的累积。

不能用暴力，否则超时

比如[1,2,3,4]
左侧数字累积是[1,1,2,6]

算完之后用一个R来保存右侧的累积，初始化R为1
虽然在第一轮中，4这个位置的左边已经全部算好了，但是我们需要改变R的累积来为3这个数字服务，所以倒着的时候还是先从最后一个数开始
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int[] productExceptSelf(int[] nums) {
        int[] result = new int[nums.length];
        result[0] = 1;
        for (int i = 1; i < nums.length; i++) {
            result[i] = result[i - 1] * nums[i - 1];
        }
        
        int Right = 1;//代表右侧数字的累积
        for (int i = nums.length - 1; i >= 0; i--) {
            result[i] = Right * result[i];
            Right = Right * nums[i];//累积
        }
        return result;
    }
}

148 排序链表 medium

和下一个方法一样的思路，但是这个方法可能好理解一点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
/*
归并排序，可以看下面一个图

切割环节：
使用 fast,slow 快慢双指针法，奇数个节点找到中点，偶数个节点找到中心左边的节点。
找到中点 slow 后，执行 slow.next = null 将链表切断
递归分割时，输入当前链表左端点 head 和中心节点 slow 的下一个节点 
cut 递归终止条件： 当head.next == None时，说明只有一个节点了，直接返回此节点

merge环节：
就是21题源代码


如果下面写成fast = head
传入head只有两个节点的时候，slow会指向第二个节点，此时left : head->node1->null ; right:null; 然后在ListNode left = sortList(head);这一步会发生stackoverflow
但是如果要用fast = head
需要把while写成while (fast != null && fast.next != null && fast.next.next != null)
*/
class Solution {
    public ListNode sortList(ListNode head) {
        // 1、递归结束条件
        if (head == null || head.next == null) {
            return head;
        }
        //  需要找到链表中间节点的前一个节点（876类似，但是又不同于876）
        ListNode slow = head;
        ListNode fast = head.next.next;//不能写成head，但是可以写成head.next，但是建议还是写成next.next，和下面对应
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        ListNode head2 = slow.next;
        slow.next=null;//切割出来

        return mergeTwoLists(sortList(head), sortList(head2));
    }
    
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {//21题原题代码
        ListNode dump = new ListNode(-1);
        ListNode cur = dump;
        while (list1 != null && list2 != null) {
            if (list1.val < list2.val) {
                cur.next = list1;
                list1 = list1.next;
            } else {
                cur.next = list2;
                list2 = list2.next;
            }
            cur = cur.next;
        }
        cur.next = list1 == null ? list2 :list1;
        return dump.next;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/*
归并排序方法
*/
class Solution {
    public ListNode sortList(ListNode head) {
        // 1、递归结束条件
        if (head == null || head.next == null) {
            return head;
        }

        // 2、找到链表中间节点并断开链表 & 递归下探
        ListNode midNode = middleNode(head);
        ListNode rightHead = midNode.next;
        midNode.next = null;

        ListNode left = sortList(head);//递归
        ListNode right = sortList(rightHead);//递归

        // 3、当前层业务操作（合并有序链表）
        return mergeTwoLists(left, right);
    }
    
    //  需要找到链表中间节点的前一个节点（876类似，但是又不同于876）
    public ListNode middleNode(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode slow = head;
        ListNode fast = head.next.next;//不能写成head，但是可以写成head.next

        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }

        return slow;
    }

    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {//21题原代码，合并两个升序链表
        ListNode dump = new ListNode(-1);
        ListNode cur = dump;
        while (list1 != null && list2 != null) {
            if (list1.val < list2.val) {
                cur.next = list1;
                list1 = list1.next;
            } else {
                cur.next = list2;
                list2 = list2.next;
            }
            cur = cur.next;
        }
        cur.next = list1 == null ? list2 :list1;
        return dump.next;
    }
}

自己写的解法，思路很简单，先用Arraylist来记录数字，然后排序，这里注意是用Collections.sort(list);进行排序，而不是Arrays.sort(list)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//不过这个不太符合题目的要求，时间和空间复杂度会很高
class Solution {
    public ListNode sortList(ListNode head) {
        ArrayList<Integer> list = new ArrayList<>();
        int len = 0;
        ListNode cur = head;
        while (cur != null) {
            list.add(cur.val);
            cur = cur.next;
        }
        
        Collections.sort(list);
        ListNode dump = new ListNode(-1);
        ListNode temp = dump;
        for (int x : list) {
            temp.next = new ListNode(x);
            temp = temp.next;
        }
        return dump.next;
    }
}

200 岛屿数量 medium

对比695

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/*
和695非常类似，一开始我用695的方法，在判断上是只要面积大于0就加1，但是感觉有点冗余，下面是去掉了冗余的代码
*/
class Solution {
    public int numIslands(char[][] grid) {
        int result = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == '1') {
                    dfs(grid, i, j);
                    result++;
                }
            }
        }
        return result;
    }
    public void dfs(char[][] grid, int cur_i, int cur_j) {
        if (cur_i < 0 || cur_j <  0 || cur_i == grid.length || cur_j == grid[0].length || grid[cur_i][cur_j] != '1')  {
            return;
        }
        grid[cur_i][cur_j] = '0';//这个很重要，把走过的格子置为0，不然会一直重复dfs

        int[] next_cur_i = {0,0,1,-1};
        int[] next_cur_j = {1,-1,0,0};
        for (int index = 0; index < 4; index++) {
            int next_i = cur_i + next_cur_i[index];
            int next_j = cur_j + next_cur_j[index];
            dfs(grid, next_i, next_j);
        }
    }
}

208 实现Trie(前缀树) medium

具体看解释看，前缀树的用处：一次建树，多次查询

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Trie {
    class TrieNode {
        private boolean isEnd;//该节点是否是一个串的结束
        TrieNode[] next;//指向孩子节点

        public TrieNode() {//初始化
            isEnd = false;
            next = new TrieNode[26];//字母映射表
        }
    }
    private TrieNode root;//指向根，后面每次操作，都是从根开始

    public Trie() {
        root = new TrieNode();
    }
    
    public void insert(String word) {//插入操作
        TrieNode node = root;//从根开始查
        for (char c : word.toCharArray()) {
            if (node.next[c - 'a'] == null) {//如果没有的话，
                node.next[c - 'a'] = new TrieNode(); //就开辟一个新的节点
            }
            node = node.next[c - 'a'];//插入完之后指向下一个节点
        }
        node.isEnd = true;//插入完之后，设置尾巴为true，表示这个词的终点
    }
    
    public boolean search(String word) {//查找操作
        TrieNode node = root;//从根开始查
        for (char c : word.toCharArray()) {
            node =  node.next[c - 'a'];//移动下一个节点
            if (node == null) {//如果空的话直接返回false
                return false;
            }
        }
        return node.isEnd;//注意因为这个是查找整个单词的操作，所以是返回尾巴的isend看看是不是为true
    }
    
    public boolean startsWith(String prefix) {//查找前缀
        TrieNode node = root;//从根开始查
        for (char c : prefix.toCharArray()) {
            node =  node.next[c - 'a'];//移动下一个节点
            if (node == null) {//如果空就直接返回false
                return false;
            }
        }
        return true;//注意这里只是查找前缀，所以如果全部都找完了，说明没有false，那么最终就是返回true
    }
}

额外练习

21 合并两个有序链表 easy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode head = new ListNode(-1);
        ListNode cur = head;
        while (list1 != null && list2 != null) {
            if (list2.val >= list1.val) {
                cur.next = list1;
                list1 = list1.next;
            } else if (list2.val < list1.val) {
                cur.next = list2;
                list2 = list2.next;
            }
            cur = cur.next;//判断完记得移到next
        }
        cur.next = list1 == null ? list2 : list1;
        return head.next;
    }
}

先递增再递减数组找最大值

别人面试碰到的题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/*
(1)如果数组先增大再减小，峰值就是最大值。
(2)如果数组单调递增，最后一个元素就是最大值。
(3)如果数组单调递减，第一个元素就是最大值。
(4)如果数组全部都一样，任何一个元素都是答案，更极端地，如果数组只有一个元素，那么这唯一的元素就是答案。

作者：analanxingde
链接：https://www.jianshu.com/p/fa328c8a323c
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
*/
int FindMax(int *A, int m)
{
    if(m == 0) return -1;            //如果数组大小为0，则返回错误
    int begin = 0;
    int end = m - 1;
    int MP =  (begin + end)/2;
    
    while(MP > 0 && MP < m -1)
    {
        if(A[MP] > A[MP+1] && A[MP] > A[MP-1]){  //如果符合条件就返回此值
                   return MP;        
          }else if (A[MP] < A[MP+1]){            //在递增段
                begin = MP+ 1;
                MP= begin + (end - begin)/2;
          }else{                                 //在递减段
                end = MP- 1;
                MP= begin + (end - begin)/2;
          }
    }
    
    if(MP == 0) return 0; //如果数组是完全递减的，则第一个值就是最大值
    if(MP == m-1) return m-1; //如果数组是完全递增的，则最后一个值为最大值
    return -1；
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int longestConsecutive(int[] nums) {
        Set<Integer>set=new HashSet<>();//HashSet 基于 HashMap 来实现的，是一个不允许有重复元素的集合。
        for(int i:nums) {
            set.add(i);
        }//将元素加入集合中
        int len=0,max=0;
        for(int i:nums) {
            if(!set.contains(i-1)){//进行判断如果有比当前元素小的元素就直接跳过不在进行长度增长。如果不进行该操作时间会超限
                while(set.contains(i)) {
                    len+=1;
                    i+=1;//取最大连续序列，就一直＋1再判断是否在序列中
                }
                if(len>max) {
                    max=len;
                }
            }
            len=0;
        }
        return max;
    }
}

作者：cranky-gausshdx
链接：https://leetcode.cn/problems/longest-consecutive-sequence/solution/by-cranky-gausshdx-jm5b/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

14 最长公共前缀 easy

注意这个题只是看前缀，而不是共同字符，所以只在最前面开始搜就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public String longestCommonPrefix(String[] strs) {
        String ans = strs[0];//把第一个字符串拿过来
        for (int i = 1; i < strs.length; i++) {//然后从第二个字符串开始比较
            int j = 0;//为什么在这里写而不是下面写？ 下面有解释
            for( ;j < ans.length() && j < strs[i].length(); j++) {
                if (ans.charAt(j) != strs[i].charAt(j)) {
                    break;
                } 
            }
            ans = ans.substring(0, j);//因为是前缀，所以肯定是从第一个开始，至于到了哪个是共同，就是看j
        }
        return ans;
    }
}

错误题解，用来解释的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/*
但是，如果下面这样写的话
["ab", "a"]的输出结果是ab，这是错误的，正确结果应该是a，因为第二个字符串长度为1，所以只进行了一次循环后，就不循环了，也就是b这个数都无法比较，所以最终无法进入if语句
*/
class Solution {
    public String longestCommonPrefix(String[] strs) {
        String ans = strs[0];
        for (int i = 1; i < strs.length; i++) {
            for(int j = 0 ;j < ans.length() && j < strs[i].length(); j++) {//如果在这里写，那么ans.sub就要在if里面写，因为是局部变量
                if (ans.charAt(j) != strs[i].charAt(j)) {
                    ans = ans.substring(0, j);
                    break;
                } 
            }
        }
        return ans;
    }
}

83 删除排序链表中的重复数字 easy

其实很简单，为什么自己一开始想的很复杂呢？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        ListNode dump = new ListNode(-1);
        dump.next = head;
        ListNode cur = head;
        while (cur != null && cur.next != null) {
            if (cur.val == cur.next.val) {
                cur.next = cur.next.next;
            } else {
                cur = cur.next;
            }
        }
        return dump.next;
    }
}

88 合并两个有序数组 easy

在尾巴处进行修改，需要注意的是，本题的nums1大小是m+n，然后最后返回的数组也是nums1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i = m - 1;
        int j = n - 1;
        int k = m + n - 1;
        while (i >= 0 && j >= 0) {
            if (nums2[j] > nums1[i]) {
                nums1[k--] = nums2[j--];
            } else {
                nums1[k--] = nums1[i--];
            }
        }
        while (j >= 0) nums1[k--] = nums2[j--];//对剩下的nums2进行操作，不需要对nums1进行操作了，因为本质上是原地复制，无意义
    }
}